How do you find the average rate of change in calculus?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Great question!
And that’s exactly what you’ll going to learn in today’s lesson.
Let’s go!
I’m sure you’re familiar with some of the following phrases:
- Miles Per Hour
- Cost Per Minute
- Plants Per Acre
- Kilometers Per Gallon
- Tuition Fees Per Semester
- Meters Per Second
How To Find Average Rate Of Change
Whenever we wish to describe how quantities change over time is the basic idea for finding the average rate of change and is one of the cornerstone concepts in calculus.
So, what does it mean to find the average rate of change?
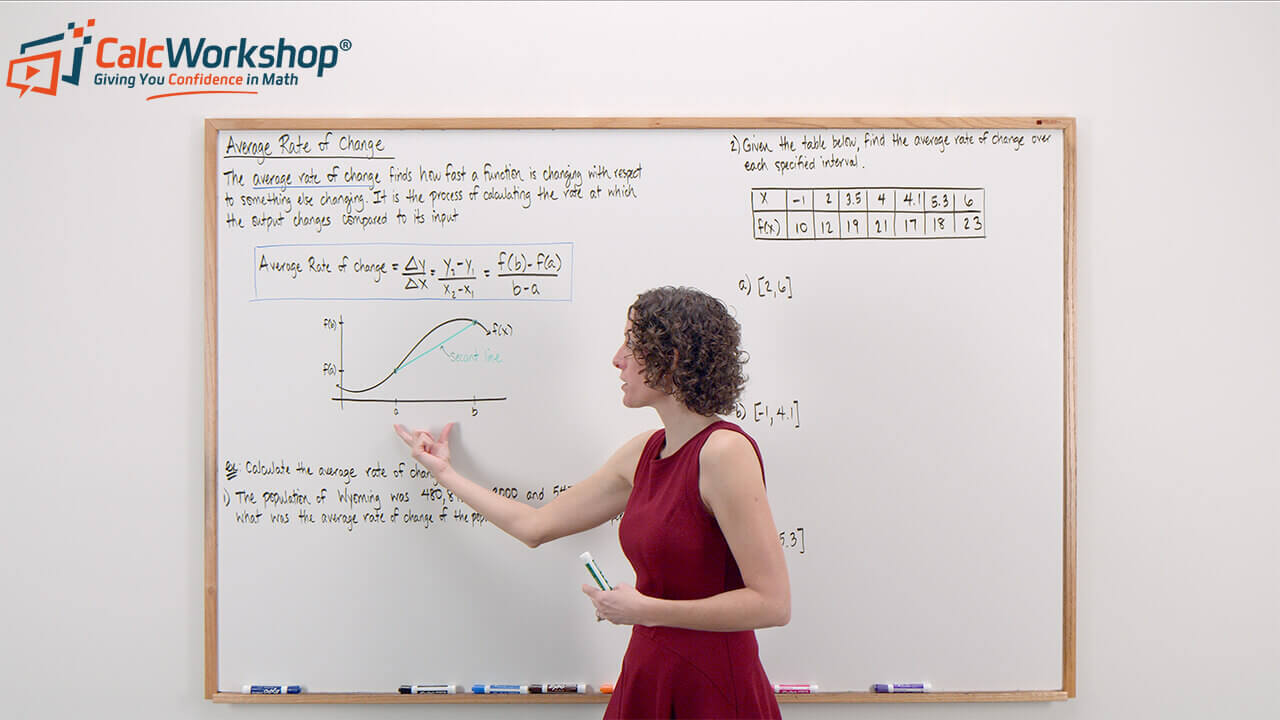
The average rate of change finds how fast a function is changing with respect to something else changing.
It is simply the process of calculating the rate at which the output (y-values) changes compared to its input (x-values).
How do you find the average rate of change?
We use the slope formula!
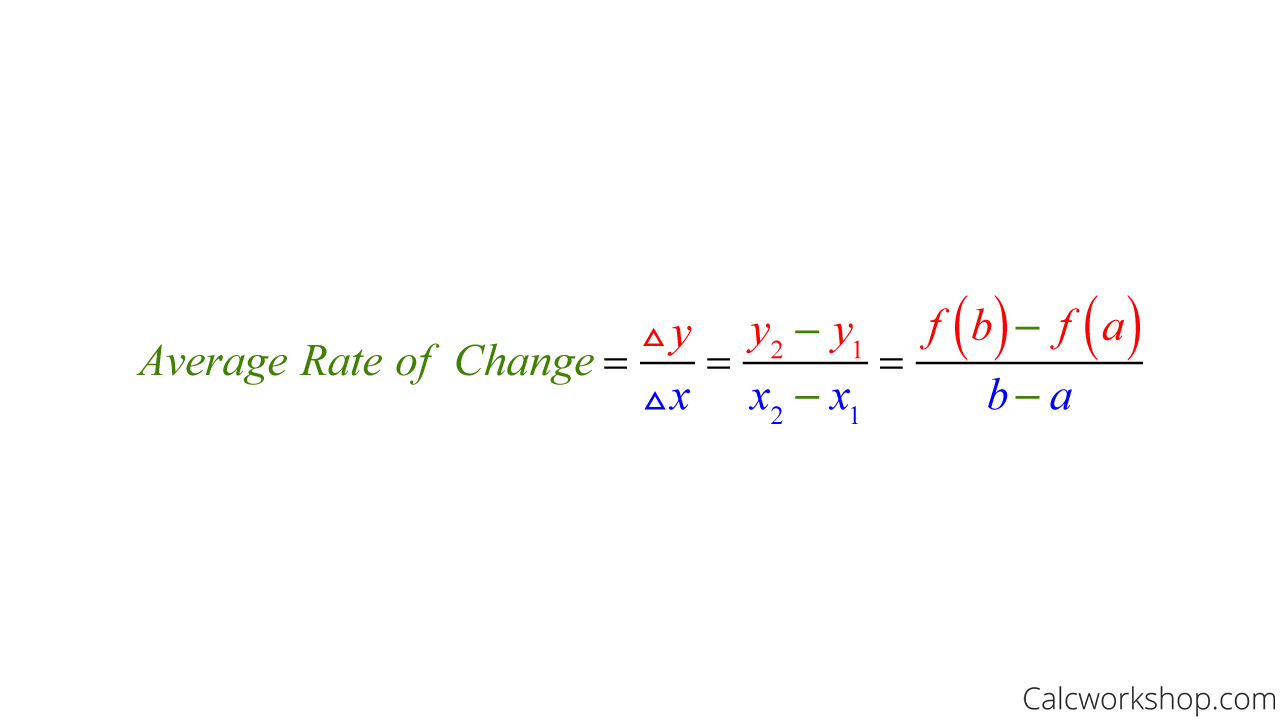
Average Rate Of Change Formula
To find the average rate of change, we divide the change in y (output) by the change in x (input). And visually, all we are doing is calculating the slope of the secant line passing between two points.
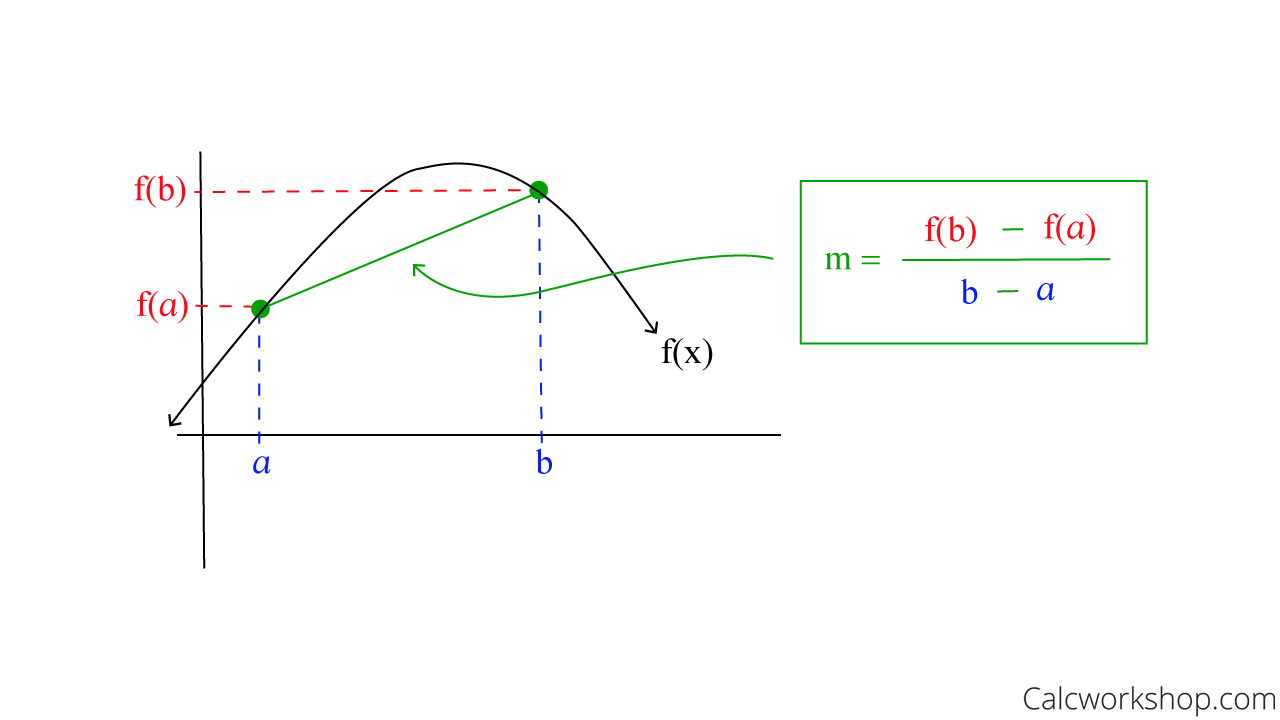
How To Find The Slope Of A Secant Line Passing Through Two Points
Now for a linear function, the average rate of change (slope) is constant, but for a non-linear function, the average rate of change is not constant (i.e., changing).
Let’s practice finding the average rate of a function, f(x), over the specified interval given the table of values as seen below.
Practice Problem #1

Find The Average Rate Of Change Of The Function Over The Given Interval
Practice Problem #2

How To Find Average Rate Of Change Over An Interval
See how easy it is?
All you have to do is calculate the slope to find the average rate of change!
Average Vs Instantaneous Rate Of Change
But now this leads us to a very important question.
What is the difference is between Instantaneous Rate of Change and Average Rate of Change?
While both are used to find the slope, the average rate of change calculates the slope of the secant line using the slope formula from algebra. The instantaneous rate of change calculates the slope of the tangent line using derivatives.
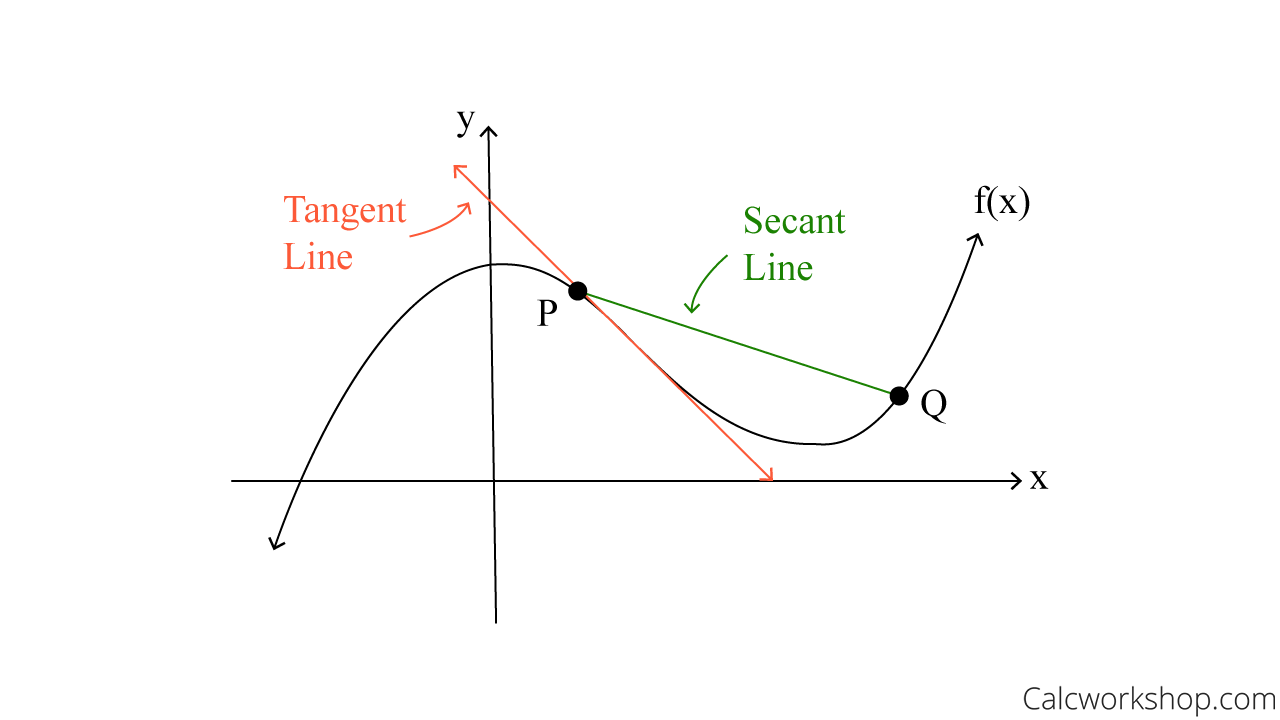
Secant Line Vs Tangent Line
Using the graph above, we can see that the green secant line represents the average rate of change between points P and Q, and the orange tangent line designates the instantaneous rate of change at point P.
So, the other key difference is that the average rate of change finds the slope over an interval, whereas the instantaneous rate of change finds the slope at a particular point.
How To Find Instantaneous Rate Of Change
All we have to do is take the derivative of our function using our derivative rules and then plug in the given x-value into our derivative to calculate the slope at that exact point.
For example, let’s find the instantaneous rate of change for the following functions at the given point.
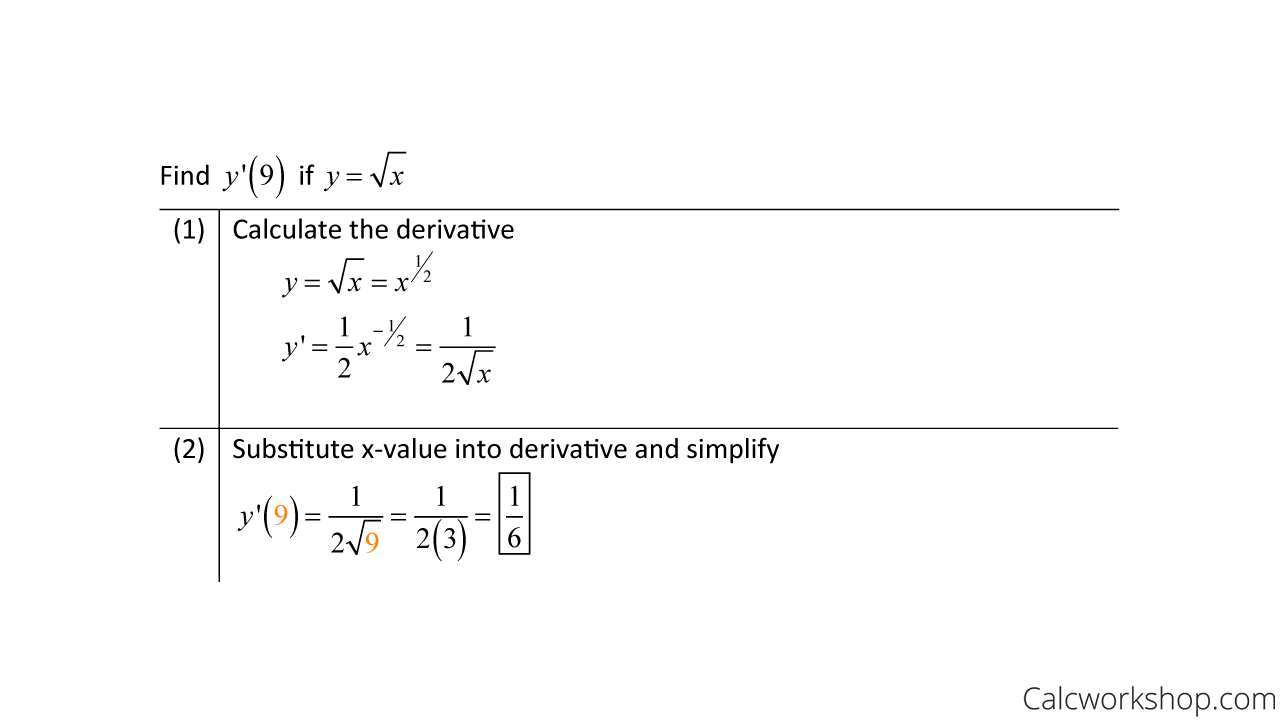
Instantaneous Rate Of Change Calculus – Example
Tips For Word Problems
But how do we know when to find the average rate of change or the instantaneous rate of change?
We will always use the slope formula when we see the word “average” or “mean” or “slope of the secant line.”
Otherwise, we will find the derivative or the instantaneous rate of change. For example, if you see any of the following statements, we will use derivatives:
- Find the velocity of an object at a point.
- Determine the instantaneous rate of change of a function.
- Find the slope of the tangent to the graph of a function.
- Calculate the marginal revenue for a given revenue function.
Harder Example
Alright, so now it’s time to look at an example where we are asked to find both the average rate of change and the instantaneous rate of change.

Average And Instantaneous Rate Of Change Of A Function – Example
Notice that for part (a), we used the slope formula to find the average rate of change over the interval. In contrast, for part (b), we used the power rule to find the derivative and substituted the desired x-value into the derivative to find the instantaneous rate of change.
Nothing to it!
Particle Motion
But why is any of this important?
Here’s why.
Because “slope” helps us to understand real-life situations like linear motion and physics.
The concept of Particle Motion, which is the expression of a function where its independent variable is time, t, enables us to make a powerful connection to the first derivative (velocity), second derivative (acceleration), and the position function (displacement).
The following notation is commonly used with particle motion.

Displacement Velocity Acceleration Notation Calculus
Ex) Position – Velocity – Acceleration
Let’s look at a question where we will use this notation to find either the average or instantaneous rate of change.
Suppose the position of a particle is given by \(x(t)=3 t^{3}+7 t\), and we are asked to find the instantaneous velocity, average velocity, instantaneous acceleration, and average acceleration, as indicated below.
a. Determine the instantaneous velocity at \(t=2\) seconds
\begin{equation}
\begin{array}{l}
x^{\prime}(t)=v(t)=9 t^{2}+7 \\
v(2)=9(2)^{2}+7=43
\end{array}
\end{equation}
Instantaneous Velocity: \(v(2)=43\)
b. Determine the average velocity between 1 and 4 seconds
\begin{equation}
A v g=\frac{x(4)-x(1)}{4-1}=\frac{\left[3(4)^{3}+7(4)\right]-\left[3(1)^{3}+7(1)\right]}{4-1}=\frac{220-10}{3}=70
\end{equation}
Avgerage Velocity: \(\overline{v(t)}=70\)
c. Determine the instantaneous acceleration at \(t=2\) seconds
\begin{equation}
\begin{array}{l}
x^{\prime \prime}(t)=a(t)=18 t \\
a(2)=18(2)=36
\end{array}
\end{equation}
Instantaneous Acceleration: \(a(2)=36\)
d. Determine the average acceleration between 1 and 4 seconds
\begin{equation}
A v g=\frac{v(4)-v(1)}{4-1}=\frac{x^{\prime}(4)-x^{\prime}(1)}{4-1}=\frac{\left[9(4)^{2}+7\right]-\left[9(1)^{2}+7\right]}{4-1}=\frac{151-16}{3}=45
\end{equation}
Average Acceleration: \(\overline{a(t)}=45\)
Summary
Together we will learn how to calculate the average rate of change and instantaneous rate of change for a function, as well as apply our knowledge from our previous lesson on higher order derivatives to find the average velocity and acceleration and compare it with the instantaneous velocity and acceleration.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.