Here’s an interesting fact: The derivative at a point is the slope of the tangent line at that point on the graph.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Why is this fascinating?
Because if we are ever asked to solve problems involving the slope of a tangent line, all we need are the same skills we learned back in algebra for writing equations of lines.
Equations Of Lines
So, what do we remember about equations for lines?
Well, they require just two elements:
- Point
- Slope
Example
For instance, if we desired to write the equation of a line given the point (6,1) and slope m = 3. All we will do is substitute the given information into the point-slope formula and simplify, as indicated below.
\begin{equation}
\begin{array}{l}
y-y_{1}=m\left(x-x_{1}\right) \text { if }(6,1) \text { and } m=3 \\
y-1=3(x-6) \\
y=3 x-17
\end{array}
\end{equation}
Equation Of Tangent Line
This means that to find the equation of a tangent line to a curve, f(x), we simply need two elements: point and slope. The only difference is that to find our slope (i.e., rate of change), we will use derivatives!
Is your mind blown yet?
Example
Alright, suppose we are asked to write the equation of the line tangent to the curve \(y=x^{2} \text { at } x=3\).
- First, we will find our point by substituting x = 3 into our function to identify the corresponding y-value.
- Next, we take the derivative of our curve to find the rate of change.
- We will then swap our given x-value into our derivative to find the slope at x = 3.
- Lastly, we will substitute our point (3,9) and slope m = 6 into the formula for point-slope form and write the equation of the tangent line.
\begin{equation}
\begin{array}{l}
f(x)=x^{2} \quad x=3 \\
f(3)=(3)^{2}=9 \\
(3,9)
\end{array}
\end{equation}
\begin{equation}
f^{\prime}(x)=2 x
\end{equation}
\begin{equation}
f^{\prime}(3)=2(3)=6
\end{equation}
\begin{equation}
\begin{array}{l}
y-y_{1}=m\left(x-x_{1}\right) \text { if }(3,9) \text { and } m=6 \\
y-9=6(x-3) \\
y=6 x-9
\end{array}
\end{equation}
See, finding the equation of the tangent line is easy!
We were able to use our algebra skills to find the equation of the line tangent to a curve.
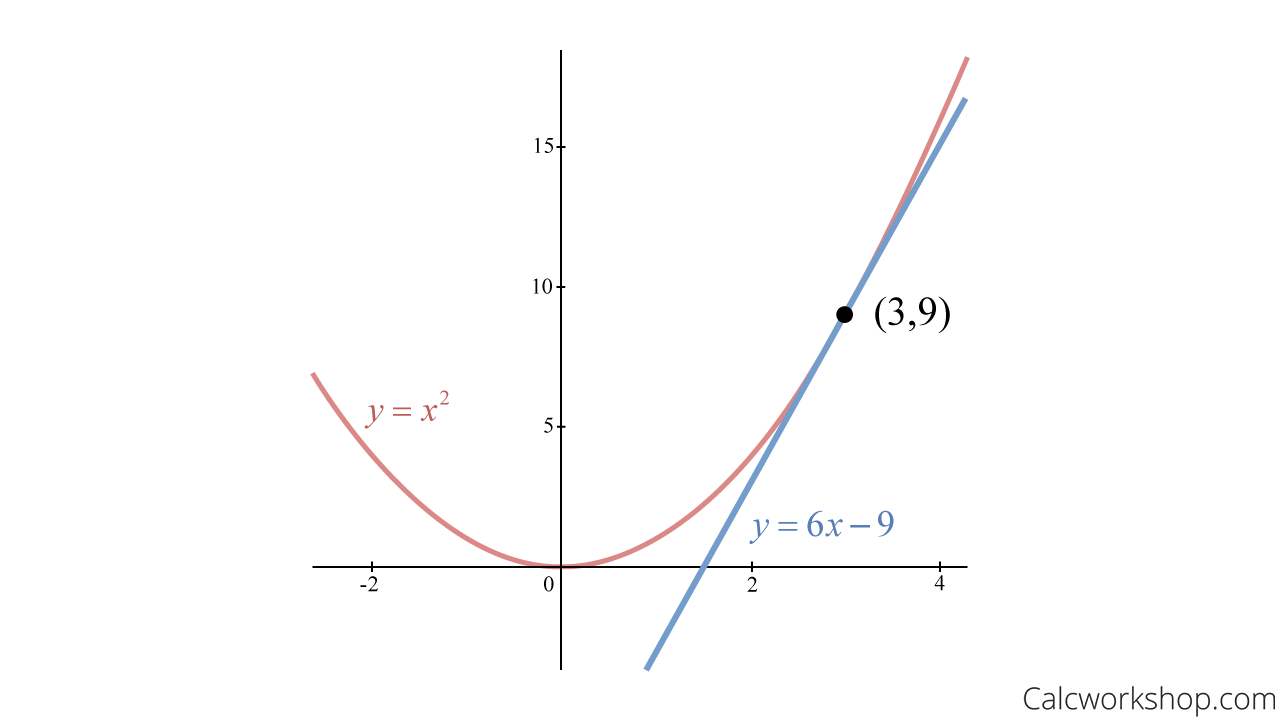
Find The Equation Of The Tangent Line
Therefore, let’s formally lay out the steps for writing the tangent line equation to a curve, as this particular skill is pivotal for future lessons dealing with linearization and differentials.
- Substitute the given x-value into the function to find the y-value or point.
- Calculate the first derivative of f(x).
- Plug the ordered pair into the derivative to find the slope at that point.
- Substitute both the point and the slope from steps 1 and 3 into point-slope form to find the equation for the tangent line.
Normal Line Equation
Likewise, we can even extend this concept to writing equations of normal lines, which are also called perpendicular lines. The only difference will be that we will simply use the negative reciprocal slope of the line tangent.
Example
For this problem, consider the curve \(f(x)=2^{3 x}\). Find the tangent line equation and normal line to f(x) at x = 1.
- First, we will find our point by substituting x = 1 into our function to identify the corresponding y-value.
- Next, we take the derivative of f(x) to find the rate of change.
- Next, we will swap our given x-value into our derivative to find the slope at x = 1.
\begin{equation}
\begin{aligned}
&f(x)=2^{3 x} \quad x=1\\
&f(1)=2^{3(1)}=8\\
&(1,8)
\end{aligned}
\end{equation}
\begin{equation}
f^{\prime}(x)=2^{3 x} \cdot \ln (2) \cdot 3
\end{equation}
\begin{equation}
f^{\prime}(1)=2^{3(1)} \cdot \ln (2) \cdot 3=24 \ln 2 \approx 16.64
\end{equation}
This means that the slope of the tangent line is 16.64, and the slope of the normal line is -1/16.64 or -0.06, which is the negative reciprocal slope!
Lastly, we will write the equation of the tangent line and normal lines using the point (1,8) and slope tangent slope of m = 16.64 and normal slope of -0.06, respectively.
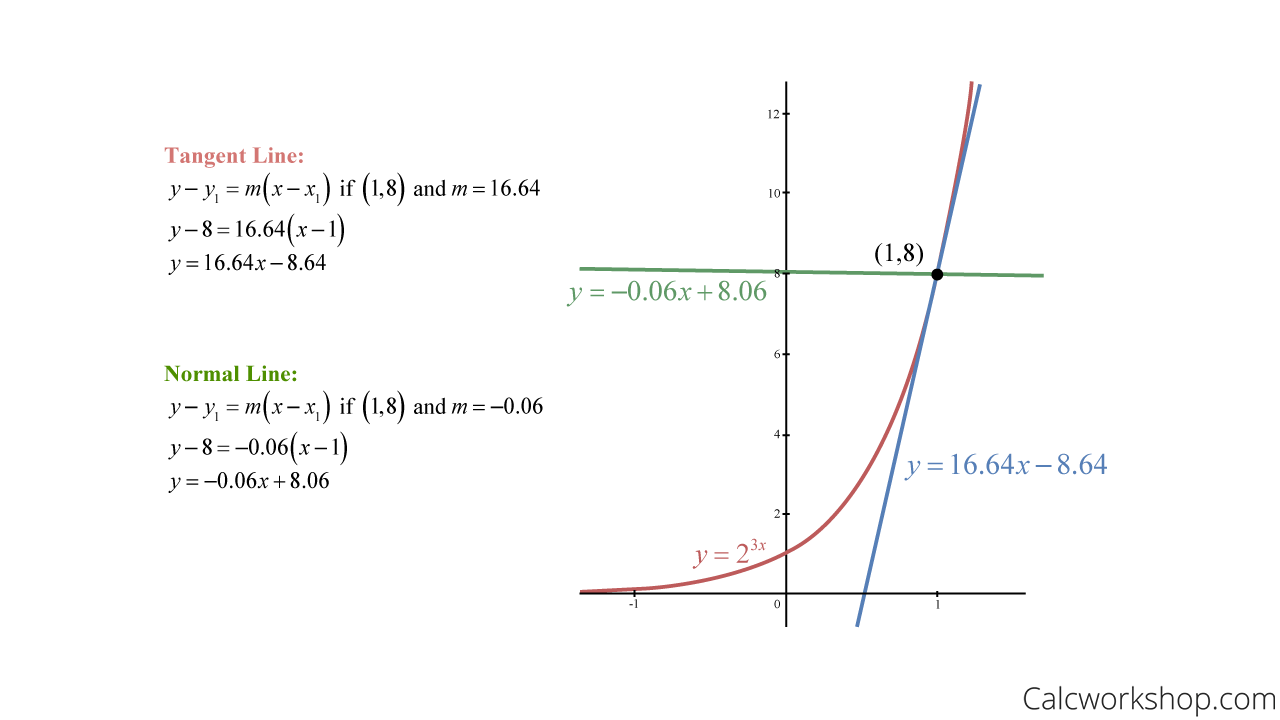
Find The Equations Of The Tangent And Normal Lines Of The Curve For A Given Point
Simple!
Together we will walk through three examples and learn how to use the point-slope form to write the equation of tangent lines and normal lines.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.