In this Algebra lesson, you’re going to learn all about the slope formula.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Did you know that slope measures the steepness of a line?
It’s true!
What is Slope?
The slope is one of the essential characteristics of a line and helps us measure the rate of change.
Another way of saying this is that the slope is the rate of change of y with respect to x.
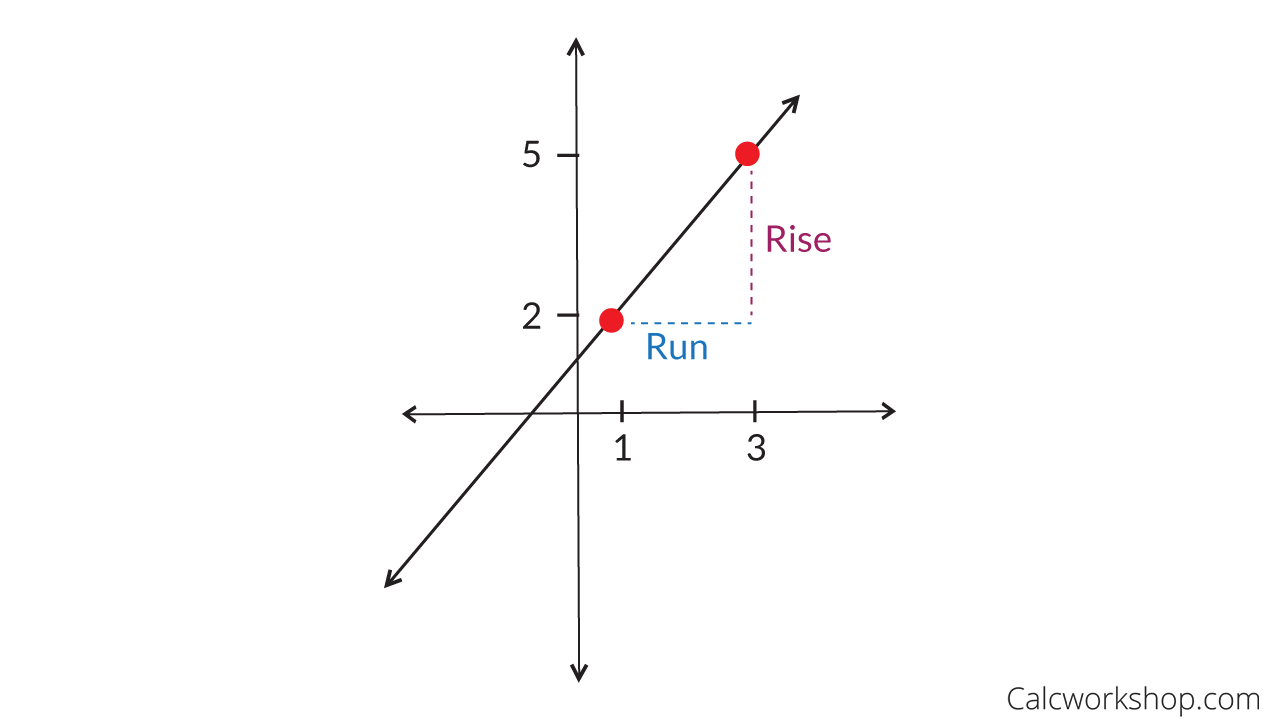
Rise Over Run
The Slope Formula!
So, here’s how it works…
…Because a line is straight, its rate of change is constant (a number).
Therefore, all we have to do is take two distinct points on a line and create a ratio of the vertical change and horizontal change.
All this means is that the slope is the fraction that represents the difference between the y-coordinates and the difference between the x-coordinates for two points on a line.

Slope Formula Definition
As we will quickly see, it does not matter which point you pick to be your “first” and which you choose to be your “second,” as Purple Math so accurately states. What is important is that you subtract your y-values and x-values in the same order and that you remain consistent.
To better understand how slope works, let’s look at a picture of slope in real life.
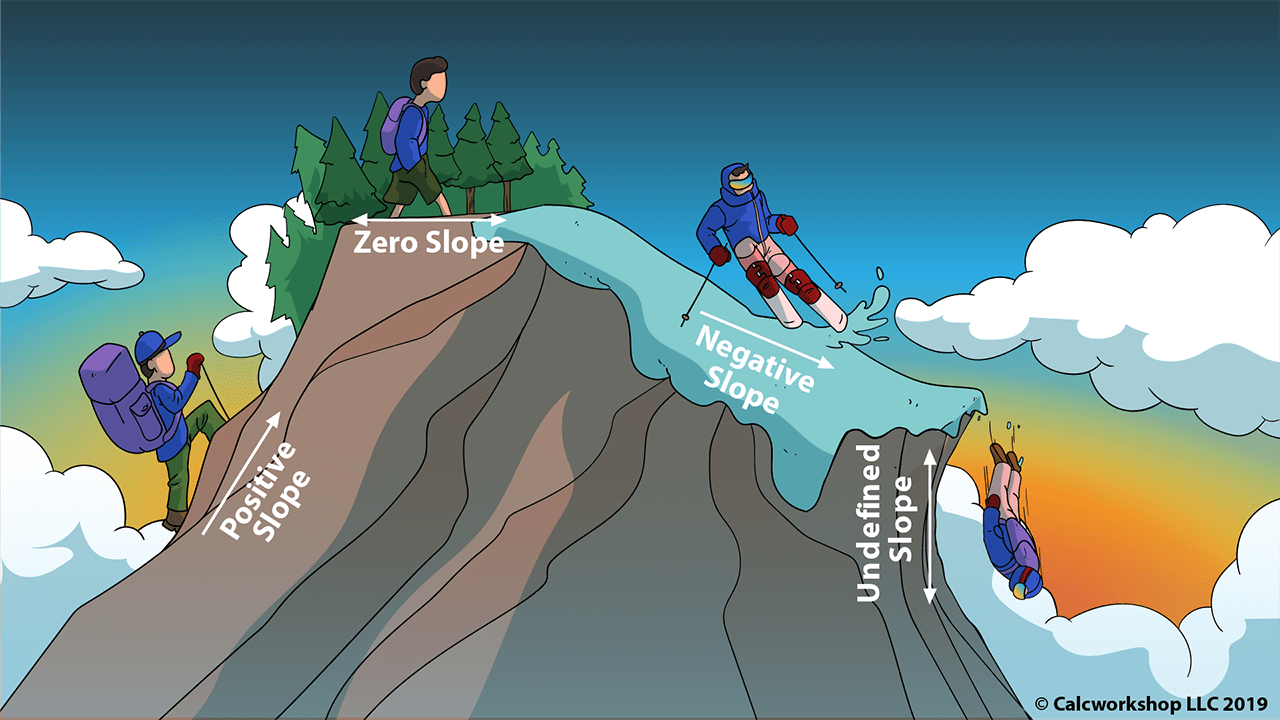
Slope in Real Life (Positive, Zero, Negative, Undefined)
Lines with Positive slope slant up to the right, whereas lines with Negative slope slant down to the right. Horizontal lines have a slope of Zero because they do not slant up or down, and a vertical line has an Undefined slope.
Example
In the example to the right, we are asked to determine the slope of the line that passes through the ordered pairs (-3,8) and (2,-11).
We first identify the components of both ordered pairs by noticing which numbers are the x-values and which are the y-values.
Then we substitute these numbers into the slope formula and calculate the slope.
Furthermore, we can interpret our answer further by noticing that the slope we calculated is negative, which indicates the line is falling from left to right.
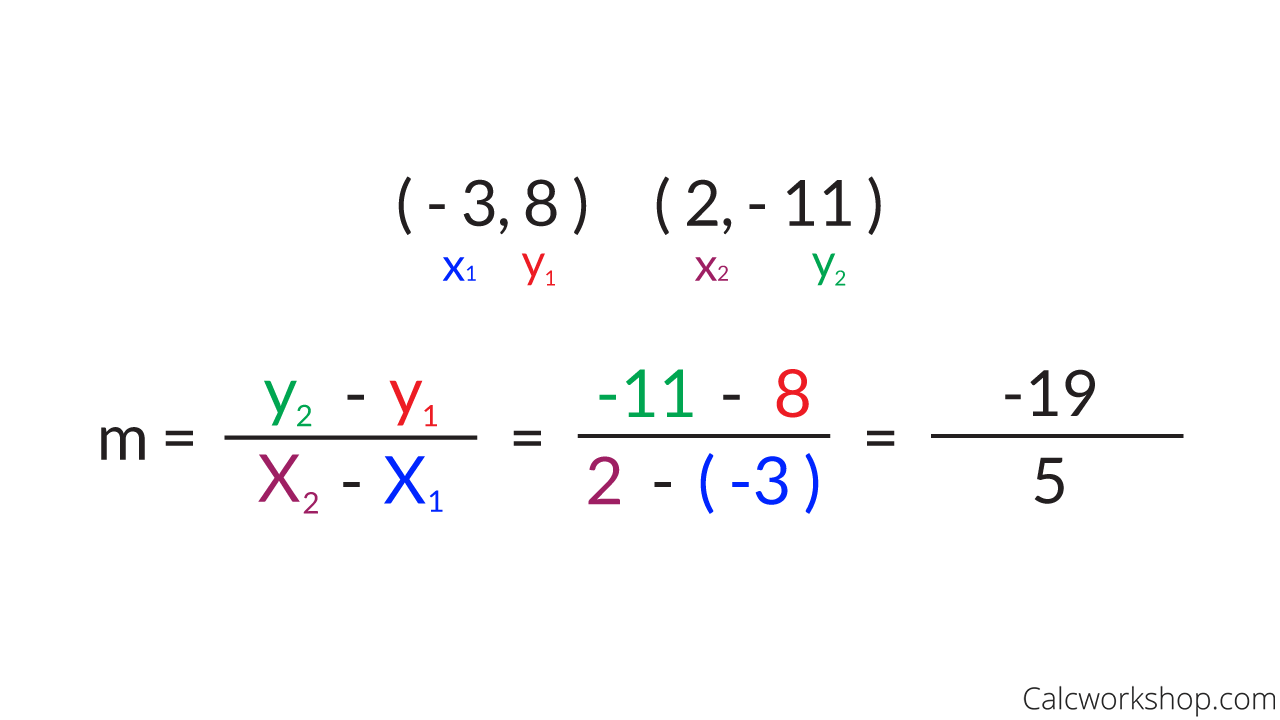
Slope Formula Example
In the video lesson below, we’ll cover harder problems so that you can feel confident in both your homework and any in class assessments. Specifically, you’ll learn how to do the following.
- Find slope using two distinct points and the slope formula.
- Calculate the slope from a graph.
- Determine the slope of each side of a given geometric figure.
Video – Lesson & Examples
1 hr 9 min
- Introduction
- 00:00:27 – What is Slope?
- Exclusive Content for Member’s Only
- 00:11:53 – Find the slope of the line through the given points (Examples #1-6)
- 00:26:24 – How to find the slope of a line on a graph (Examples #7-10)
- 00:41:29 – Find the slope of each side of the given geometric shape (Examples #11-12)
- 01:52:41 – How to find the slope of the sides of a polygon (Example #13)
- 01:01:48 – Find “y” so that the line containing the points has the indicated slope (Examples #14)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.