What’s the difference between line integrals and surface integrals?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
A line integral evaluates a function of two variables along a line, whereas a surface integral calculates a function of three variables over a surface.
And just as line integrals has two forms for either scalar functions or vector fields, surface integrals also have two forms:
- Surface integrals of scalar functions.
- Surface integrals of vector fields.
Let’s take a closer look at each form of the surface integral.
Scalar Field
The surface integral of a function
…where
But sometimes, even this formula is difficult to calculate.
Thankfully, we have another trick up our sleeves…
…Parameterization!
Parametric Surface
Let’s see how to compute the surface integral of a function over a parametric surface.
Let
Example
Let’s look at an example.
Compute the surface integral of
First, we need to find our first order partials.
Next, we will compute the cross product
.
Now we will find the magnitude of the cross product
.
Now we will parameterize our integrand.
If
and , then
Lastly, we substitute everything into our surface integral formula and solve.
And that’s it.
All we have to do is follow the steps.
Surface Integral Orientation
Now it’s time to turn our attention to vector fields and the flow of vector fields through permeable surfaces placed in the field.
But before we do, we need to talk about orientation. In particular, finding the positive orientation for a closed-oriented surface.
Alright, so most surfaces have two sides (i.e., inside and outside), but some surfaces, such as a Mobius strip, are only one-sided and thus deemed nonorientable.

Mobius Strip
Thankfully, we will strictly be dealing with orientable or two-sided surfaces!
Why?
Because they come armed with a unit normal vector that provides two orientations for a surface quite nicely.
For a surface
And a parametric smooth surface
So, for a surface that is the boundary of a solid E (i.e., closed surface), the convention is that the positive orientation is the one for which the normal vectors point outward from
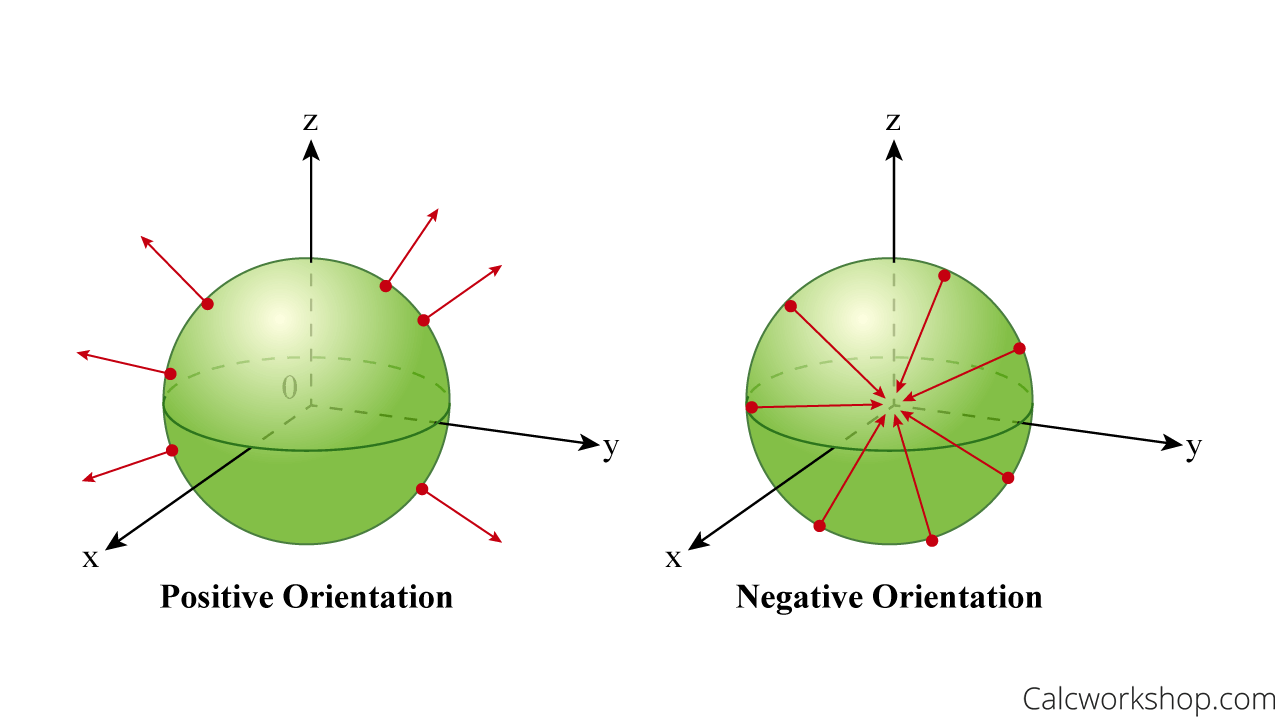
Surface Integral Orientation
Vector Fields
Okay, so now we are ready to talk about surface integrals of vector fields!
If
This integral is also called the flux of
Why?
Because the surface integral of a vector field represents the amount of fluid flowing through the surface per unit of time:
So, if a surface integral measures the total rate of flow, then we can simply call it a flux integral, because that’s exactly what we are calculating…the flux!
But once again, our current formula is still a bit difficult to use. Thankfully, there is an alternate form for calculating the flux integral.
Flux Integral – Alternate Form
Suppose
OR
And together, we will learn how to use these formulas to evaluate the flux of a vector field across a surface in our video lesson.
So, together we will learn why we use surface integrals and which form or formula to utilize when finding the flow rate across a surface.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.