So what is the purpose of a line integral?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
To illustrate the idea, think about how it feels to run on a track on a windy day or to row a boat across a lake with a noticeable current?
The path of the wind or the flow of the current might make it easier in one direction than the other, right?
Interestingly, a line integral can help us map out where we benefited from the wind or the current and where those same forces hindered our progress.
How’s is this possible?
Let’s find out…
Line Integral
A line integral, called a curve integral or a path integral, is a generalized form of the basic integral we remember from calculus 1. But instead of being limited to an interval, [a,b], along the x-axis, we can explain more general curves along any path in the plane.
How?
By “straightening” out the path using parameterization and arc length.
Let’s shed some more light on this…
w/ Two Functions
Suppose we have a smooth curve \(C\) in the plane, and it is given by the vector equation in parameterized form:
\begin{equation}
\vec{r}(t)=\langle x(t), y(t)\rangle \text { from } a \leq t \leq b
\end{equation}
where \(\vec{r}^{\prime}(t)\) is continuous and \(\vec{r}^{\prime}(t) \neq \overrightarrow{0}\).
The line integral of \(f\) along the curve \(C\) from \(a\) to \(b\) is defined as \(\int_C {f\left( {x,y} \right)ds} \) where \(ds\) is the arc length differential.
Thus, if \(C\) is a plane curve parameterized by \(x\left( t \right)\) and \(y\left( t \right)\) from \(a \le t \le b\), then we can say that the line integral \(f\) along \(C\) is:
\begin{equation}
\int_{C} f(x, y) d s=\int_{a}^{b} f(x(t), y(t)) \sqrt{\left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}} d t
\end{equation}
w/ Three Functions
And in three variables, if \(C\) is a plane curve given by the vector equation \(\overrightarrow r \left( t \right) = \left\langle {x\left( t \right),y\left( t \right),z\left( t \right)} \right\rangle \) the line integral is:
\begin{equation}
\int_{C} f(x, y, z) d s=\int_{a}^{b} f(x(t), y(t), z(t)) \sqrt{\left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}+\left(z^{\prime}(t)\right)^{2}} d t
\end{equation}
And here’s the key to evaluating line integrals \(\int_C {f\left( {x,y} \right)ds} \)…
…parameterize \(C\).
Example
Let’s look at an example.
Evaluate \(\int_C {\left( {xy + {z^3}} \right)} ds\), where \(C\) is the part of the helix \(\overrightarrow r \left( t \right) = \left\langle {\cos t,\sin t,t} \right\rangle \) from \(0 \le t \le \pi \).
Alright, so the first thing we’re going to do is find \(\overrightarrow r ‘\left( t \right)\).
\begin{equation}
\frac{d}{d t}[\vec{r}(t)]=\langle-\sin t, \cos t, 1\rangle
\end{equation}Next, we will calculate our arc length.
\begin{equation}
\left\|\vec{r}^{\prime}(t)\right\|=\sqrt{\left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}+\left(z^{\prime}(t)\right)^{2}}
\end{equation}\begin{equation}
\left\|\vec{r}^{\prime}(t)\right\|=\sqrt{(-\sin t)^{2}+(\cos t)^{2}+(1)^{2}}
\end{equation}\begin{equation}
=\sqrt{\sin ^{2} t+\cos ^{2} t+1}
\end{equation}\begin{equation}
=\sqrt{\underbrace{\left(\sin ^{2} t+\cos ^{2} t\right)}_{1}+1}
\end{equation}\begin{equation}
=\sqrt{1+1}
\end{equation}\begin{equation}
=\sqrt{2}
\end{equation}Now, we will write \(\overrightarrow r \left( t \right)\) in its parametrized form:
\begin{equation}
x=\cos t, \quad y=\sin t, \quad z=1
\end{equation}and substitute into our function \(f(x, y, z)=x y+z^{3}\).
\begin{equation}
f(x, y, z)=(\cos t)(\sin t)+(t)^{3}=\cos t \sin t+t^{3}
\end{equation}Finally, we are ready to substitute everything into our line integral formula and integrate it over our interval.
\begin{equation}
\int_{C} f(x, y, z) d s
\end{equation}\begin{equation}
=\int_{a}^{b} f(x(t), y(t), z(t)) \sqrt{\left(x^{\prime}(t)\right)^{2}+\left(y^{\prime}(t)\right)^{2}+\left(z^{\prime}(t)\right)^{2}} d t
\end{equation}\begin{equation}
\int_{0}^{\pi}\left(\cos t \sin t+t^{3}\right)(\sqrt{2}) d t
\end{equation}\begin{equation}
\sqrt{2} \int_{0}^{\pi}\left(\cos t \sin t+t^{3}\right) d t
\end{equation}\begin{equation}
\sqrt{2}\left[\int_{0}^{\pi}(\cos t \sin t) d t+\int_{0}^{\pi}\left(t^{3}\right) d t\right]
\end{equation}\begin{equation}
\sqrt{2}\left[\int_{0}^{\pi}(\cos t \sin t) d t+\int_{0}^{\pi}\left(t^{3}\right) d t\right]
\end{equation}\begin{equation}
=\sqrt{2}\left[0+\frac{\pi^{4}}{4}\right]
\end{equation}\begin{equation}
=\frac{\pi^{4} \sqrt{2}}{4}
\end{equation}
Cool.
Piecewise (Smooth Curves)
And we can extend this idea of line integrals for piecewise, smooth curves where we define the integral of \(f\) along \(C\) as the sum of the integrals along each of the smooth pieces of C, such that:
\begin{equation}
\int_{C} f(x, y, z) d s=\int_{C_{1}} f(x, y, z) d s+\int_{C_{2}} f(x, y, z) d s+\cdots+\int_{C_{n}} f(x, y, z) d s
\end{equation}
Don’t worry.
In our video lesson, we will look at an example of how to evaluate a line integral for when \(C\) is a piecewise smooth curve.
Using Line Integral To Find Work
But the real superpower of line integrals is its ability to determine the work done by a force or work along a trajectory.
Vector Fields
So, let’s turn our attention to line integrals of vector fields.
From our previous study of vectors and work from single variable calculus, we know that the work done by the force \(\overrightarrow F \) on an object is found by \(W = \overrightarrow F \cdot \Delta \overrightarrow r \).
Thus, if we let \(\vec F\) be a continuous vector force field defined on a smooth curve \(C\) parameterized by a vector function \(\vec{r}(t)\) from \(a \le t \le b\). Then the line integral of \(\vec F\) along \(C\) is:
\begin{equation}
\int_{C} \vec{F} \cdot d \vec{r}=\int_{C} \vec{F} \cdot \vec{T} d s=\int_{0}^{b} \vec{F}(\vec{r}(t)) \cdot \vec{r}^{\prime}(t) d t=\int_{C} P d x+Q d y+R d z
\end{equation}
How to use this line integral formula to find the work done by a vector field or force field \(\vec F\) in moving an object along a vector?
Well, the steps are really quite easy.
- Find a parameterization \(\vec r\left( t \right)\) for the curve \(C\) for interval t.
- Find the tangent vector.
- Substitute the parameterization into \(\vec F\).
- Take the dot product of the force and the tangent vector.
- Integrate the work along the section of the path from \(t = a\) to \(t = b\).
Example
Okay, let’s look at an example and apply our steps to obtain our solution.
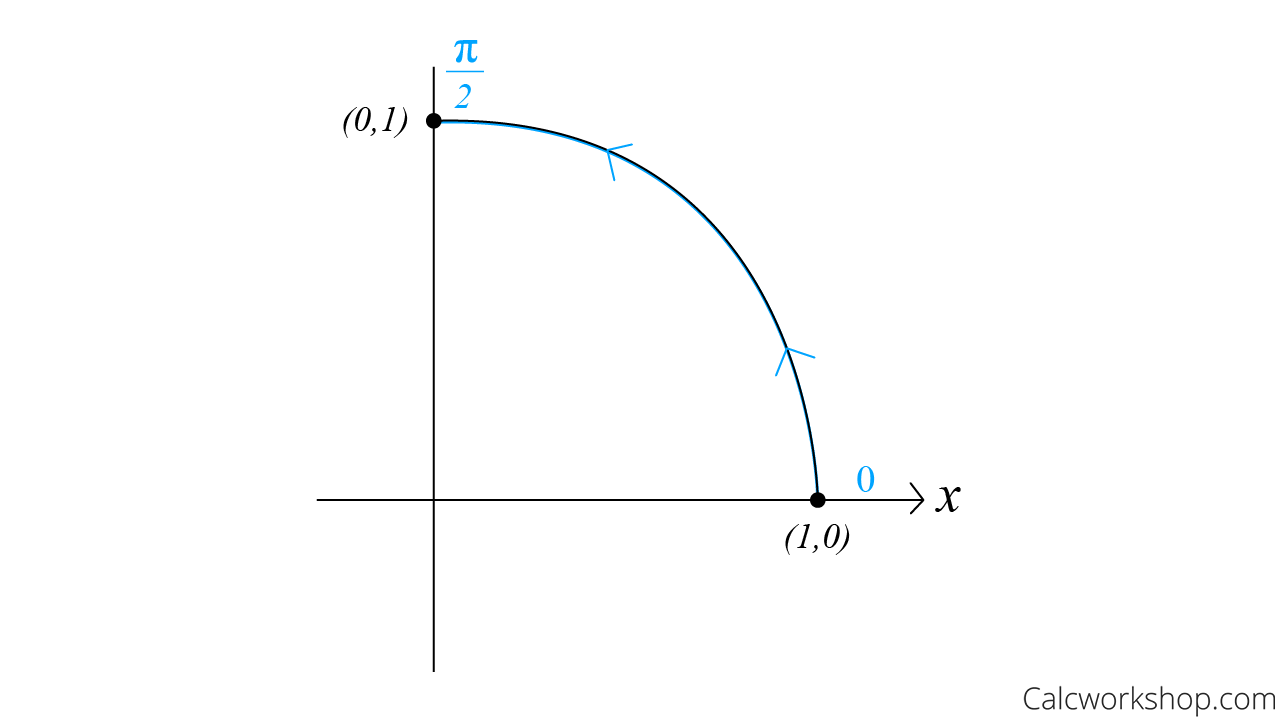
Find the work done by the force \(\vec F\left( {x,y} \right) = \left\langle {{x^2}, – xy} \right\rangle \) in moving a particle from \(\left( {1,0} \right)\) to \(\left( {0,1} \right)\) along the unit circle.
First, we will parameterize our curve using:
\begin{equation}
\vec{r}(t)=\langle x(t), y(t)\rangle=\langle\cos t, \sin t\rangle
\end{equation}\begin{equation}
\vec{F}(x, y)=\left\langle x^{2},-x y\right\rangle \Rightarrow \vec{F}=\left\langle(\cos t)^{2},-(\cos t)(\sin t)\right\rangle
\end{equation}\begin{equation}
\vec{F}=\left\langle\cos ^{2} t,-\cos t \sin t\right\rangle
\end{equation}Now we will find \(\vec r’\left( t \right)\) as our formula \(\int_C {Pdx + Qdy} \) requires \(dx\) and \(dy\).
\begin{equation}
\vec{r}^{\prime}(t)=\langle-\sin t, \cos t\rangle \text { or } \frac{d x}{d t}=-\cos t \text { and } \frac{d y}{d t}=\cos t
\end{equation}Next, we will find our limit bounds knowing that we are traveling along the unit circle from \(\left( {1,0} \right)\) to \((0,1)\). Hence, \(0 \le t \le \frac{\pi }{2}\).
Travel Parameterized Unit Circle
Now, all we have to do is substitute everything into our line integral for vector fields formula and integrate.
\begin{equation}
W=\int_{C} \vec{F} \cdot d \vec{r}=\int_{C} P d x+Q d y
\end{equation}\begin{equation}
=\int_{0}^{\frac{\pi}{2}}\left(\cos ^{2} t\right)(-\sin t) d t+(-\cos t \sin t)(\cos t) d t
\end{equation}\begin{equation}
=\int_{0}^{\frac{\pi}{2}}\left(-\cos ^{2} t \sin t\right) d t+\left(-\cos ^{2} t \sin t\right) d t
\end{equation}\begin{equation}
=\int_{0}^{\frac{\pi}{2}}\left(-2 \cos ^{2} t \sin t\right) d t
\end{equation}Apply u-substitution by letting \(u=\cos t\) with \(d u=-\sin t d t\).
\begin{equation}
=\int_{0}^{\frac{\pi}{2}}\left(-2 \cos ^{2} t \sin t\right) d t
\end{equation}\begin{equation}
W=-\frac{2}{3}
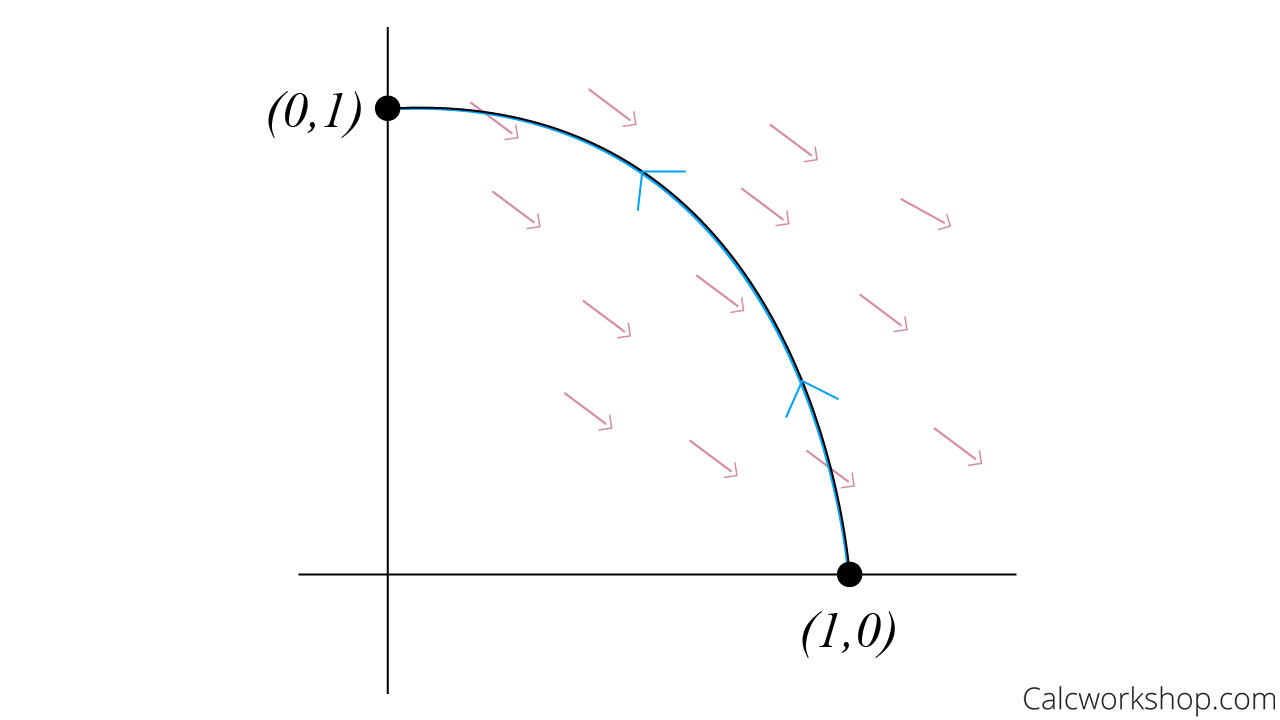
\end{equation}And with a negative result, this tells us the vector field (depicted in red in the graphic below) hinders or impedes the movement along the blue curve.
Vector Field Impacts Movement
We will unpack a lot in this lesson, as line integrals have countless applications since they will help us find out how much work a force field does when moving an object along a curve.
Let’s get started.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.