Fundamental Theorem Of Line Integrals (w/ Step-by-Step Examples!)

What determines the work performed by a vector field?

Jenn (B.S., M.Ed.) of Calcworkshop® teaching fundamental theorem of line integrals

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

Does the work only depend on the endpoints, or does changing the path while keeping the endpoints fixed make a difference?

In other words, knowing that a line integral gives us insight as to the work performed by a vector field on an object moving along a parametric curve $C$ , would the work change if we altered the course but kept the endpoints the same?

To answer such a question, we need the fundamental theorem of line integrals and a look into a special type of vector field called conservative vector fields.

Let’s investigate.

Fundamental Theorem Of Line Integrals

Think about a smooth curve $C$ given by the vector equation $\vec{r} (t)$ from $t \in [a, b]$ and a differentiable function $f$ of two or three variables whose gradient vector $\nabla f$ is continuous on $C$ .

$Then \int_{C} \nabla f \cdot d \vec{r} = \int_{a}^{b} \nabla f (\vec{r} (t)) \cdot {\vec{r}}^{'} (t) d t = f (\vec{r} (b)) - f (\vec{r} (a))$

Notice how this is just an extension of the fundamental theorem of calculus (FTC) to line integrals.

In fact, this is explicitly saying that a line integral in a conservative vector field is independent of path.

Path Independence Of Line Integrals

Let me explain further.

Recall from our lesson on vector fields, $\vec{F}$ is called a conservative vector field, or a gradient vector field, if $\vec{F} = \nabla f$ where $f$ is called the potential function of $\vec{F}$ .

But here’s what cool. The fundamental theorem for line integrals states that $\vec{F} = \nabla f$ if and only if $\int_{C} \vec{F} \cdot d \vec{r}$ is independent of path

But what does path independence really mean?

Suppose $C_{1}$ and $C_{2}$ are two different piecewise smooth curves that have the same initial point $A$ and terminal point $B$ , as shown in the graphic below.

Path Independence Line Integrals

The starting point and stopping point are fixed, but the path or route we take to get from point A to point B is different.

But here’s what’s important…it doesn’t matter what path we choose because they both start and stop at the same place.

So, if a vector field is path-independent, then

$\int_{C_{1}} \vec{F} \cdot d \vec{r} = \int_{C_{2}} \vec{F} \cdot d \vec{r}$

More specifically…

$\int_{A}^{B} \vec{F} \cdot d \vec{r} = f (B) - f (A)$

Regardless of whether you take path $C_{1}$ or $C_{2}$ .

This means we can now easily answer our earlier question.

In a conservative force field, the amount of work required to move an object from point $a$ to point $b$ only depends on those two endpoints, not on the path taken between them.

Cool, right?

Please note that in a non-conservative vector field (i.e., a general vector field), $\int_{C_{1}} \vec{F} \cdot d \vec{r} \neq \int_{C_{2}} \vec{F} \cdot d \vec{r}$ but in a conservative vector field, for any two paths $C_{1}$ and $C_{2}$ that have the same starting and ending points, then $\int_{C_{1}} \vec{F} \cdot d \vec{r} = \int_{C_{2}} \vec{F} \cdot d \vec{r}$ .

Example

Let’s look at an example.

Suppose $\vec{F} = ⟨ 12 x^{2} + 3 y^{2} + 5 y, 6 x y - 3 y^{2} + 5 x ⟩$ , knowing that $\vec{F}$ is conservative and independent of path with potential function $f (x, y) = 4 x^{3} + 3 y^{2} x + 5 x y - y^{3}$ .

Calculate $\int_{C} \vec{F} \cdot d \vec{r}$ where $C$ is any path from $(0, 0)$ to $(2, 1)$ .

Because we know that $\vec{F}$ is conservative and independent of the path, we can use the fundamental theorem of line integrals.

$\int_{C} \vec{F} \cdot d \vec{r} = \int_{C} \nabla f (\vec{r} (t)) \cdot d \vec{r} = f (B) - f (A)$

$\int_{C} \vec{F} \cdot d \vec{r} = \int_{(0, 0)}^{(2, 1)} \vec{F} \cdot d \vec{r}$

$= {f (x, y) |}_{(0, 0)}^{(2, 1)}$

$= f (2, 1) - f (0, 0)$

$= {(4 x^{3} + 3 y^{2} x + 5 x y - y^{3}]}_{(0, 0)}^{(2, 1)}$

$= (4 (2)^{3} + 3 (1)^{2} (2) + 5 (2) (1) - (1)^{3}) - 0$

$= 47$

Isn’t this a fantastic concept?

Because as Paul’s Online Notes so accurately summarizes, we now see that for these kinds of line integrals, we didn’t need to know the curve to get the answer because if we can prove the independence of path, we can use any path we want, and we’ll always get the same results.

Is A Vector Field Conservative?

But how do we determine whether a vector field is conservative and thus independent of the path?

Well, as it turns out, the only vector fields that are conservative satisfy the following theorem:

Suppose $\vec{F}$ is a vector field that is continuous on a region $D$ , where $D$ is open and connected. $\int_{C} \vec{F} \cdot d \vec{r}$ is independent of path if and only if $\int_{C} \vec{F} \cdot d \vec{r} = 0$ for every closed path $C$ . And if $\int_{C} \vec{F} \cdot d \vec{r}$ is independent of path in $D$ , then $\vec{F}$ is a conservative vector field in $D$ and there exists a function $f$ such that $\vec{F} = \nabla f$ .

While this is all well and good and extremely important to note about conservative vector fields, it’s not a useful computational tool.

Thankfully, there’s an easy way for us to determine if $\vec{F}$ is conservative!

Assume $\vec{F} = ⟨ P, Q ⟩$ is a vector field on region $D$ and that $P$ and $Q$ have continuous first order partial derivatives. Then $\vec{F}$ is conservative if and only if $P_{y} = Q_{x}$ .

And for three-dimensional vector fields such as $\vec{F} = ⟨ P, Q, R ⟩$ where $P$ , $Q$ , and $R$ have continuous first partials then $\vec{F}$ is conservative if and only if $c u r l \vec{F} = \nabla \times \vec{F} = \vec{0}$

$curl \vec{F} = \nabla \times \vec{F} = | \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{array} |$

We will predominately work with two-dimensional vector fields and leave three-dimensional vector fields, and the concept of the “curl” for a later lesson.

Example

Okay, so let’s put our new theorem to work with an example.

Is $\vec{F} = ⟨ 12 x^{2} + 3 y^{2} + 5 y, 6 x y - 3 y^{2} + 5 x ⟩$ conservative?

First, we identify $P$ and $Q$ .

$\vec{F} = ⟨ \underset{P}{\underset{⏟}{12 x^{2} + 3 y^{2} + 5 y}}, \underset{Q}{\underset{⏟}{6 x y - 3 y^{2} + 5 x}} ⟩$

Next, we take our partial derivatives and check to see that they are equal.

$P_{y} = 6 y + 5 and Q_{x} = 6 y + 5$

Because $P_{y} = Q_{x}$ we know that $\vec{F}$ is conservative.

Easy!

Finding Potential Functions

And now that we know how to determine whether or not a vector field is independent of path, we now need to learn how to find a potential function.

There are several ways this can be computed, but the easiest method is the one outlined below:

Show that $\vec{F}$ is conservative on $R^{2}$ by checking that $P_{y} = Q_{x}$ or conservative on $R^{3}$ by confirming that $c u r l \vec{F} = \nabla \times \vec{F} = \vec{0}$ .
Find $f$ by integrating $P$ with respect to $x$ and $Q$ with respect to $y$ , separately.
All terms create the potential function $f$ , however, any duplicate terms are only considered once.

While these steps may seem strange at first, I promise you that they are pretty easy to perform.

Example

Let’s work through an example to see how.

Given $\vec{F} = ⟨ 12 x^{2} + 3 y^{2} + 5 y, 6 x y - 3 y^{2} + 5 x ⟩$ , find $f$ such that $\nabla f = \vec{F}$ .

First, we must confirm that $\vec{F}$ is a conservative vector field.

$\begin{aligned} \vec{F} = ⟨ \underset{P}{\underset{⏟}{12 x^{2} + 3 y^{2} + 5 y}}, \underset{Q}{\underset{⏟}{6 x y - 3 y^{2} + 5 x}} ⟩ \\ P_{y} = 6 y + 5 = Q_{x} \end{aligned}$

Next, we will integrate $P$ with respect to $x$ and $Q$ with respect to $y$ .

$\begin{array}{cc} \int (12 x^{2} + 3 y^{2} + 5 y) d x & \int (6 x y - 3 y^{2} + 5 x) d y \\ = 4 x^{3} + 3 x y^{2} + 5 x y & = 3 x y^{2} - y^{3} + 5 x y \end{array}$

Now, all we have to do is put our terms together, only counting duplicate terms once.

$\begin{array}{cc} \int (12 x^{2} + 3 y^{2} + 5 y) d x & \int (6 x y - 3 y^{2} + 5 x) d y \\ = 4 x^{3} + \underset{―}{3 x y^{2}} + 5 x y & = \underset{―}{3 x y^{2}} - y^{3} + \underset{―}{\underset{―}{5 x y}} \end{array}$

$f (x, y) = 4 x^{3} - y^{3} + 3 x y^{2} + 5 x y + c$ , where $c$ is a constant.

That’s it!

And our solution can be easily verified as true by checking that $\nabla f = \vec{F}$ !

Together we will learn how to prove a vector field is conservative; thus, showing path independence, find a potential function $f (x, y)$ , and then evaluate using the Fundamental Theorem of line integrals.

Video Tutorial w/ Full Lesson & Detailed Examples (Video)

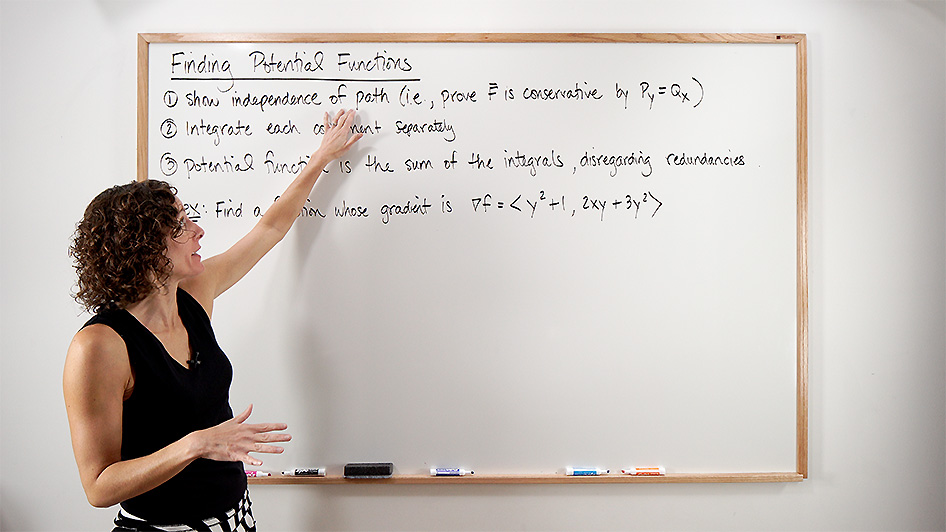
Fundamental-Theorem-for-Line-Integrals-Example

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.

4.9 / 5

1,127 Reviews

Kevin S.10-30-24 - CO, United States

I had never even heard of discrete math before I had to take it for my Bachelor's in Cybersecurity. I had actually hoped that my math days were done! I suffered through class not understanding any of the presentations until I stumbled across Calcworkshop. I used the Calcworkshop lessons more than I used my instructor's lectures and my book. I ended up with a high B (just 12 points away from an A) thanks to Jenn. Without her easy to understand style of teaching, I'm not sure I would have even passed the class. Thank you so much!!!

Richard10-29-24 - Norway

Very well structured and site. It is well structured giving a good overview of the different topics regarding all mathematics where you easily can choose which path is applicable to your specific needs.The video lectures are superb with introduction to the topic followed by a detailed theoretically explaination and what I personally get most out of is; heaps of examples where you are taken and shown, step by step, the prosess of solving the problem. They also includd practice sheets and solutions to test yourself after each chapter. There is a lot to undertake on this site, but it provides an easy and understandable interface to map out what you need to do. The site has been very helpfull for me and I highly recommend it.

RobWP10-26-24 - United States

I am taking this course for mainly linear algebra review. It is a course that I have had but fairly long ago. I'm currently working in masters in data science and linear algebra namely transformations is something that has come up and I thought I need a good review on. I so far what I have liked about the course is, the common sense approach. Her approach makes it easy to remember the concepts because of her common sense approach. I like the fact that she gives information that is not really in any textbooks. I can vouch for that because not only have I used textbook recently to review I have had a formal class in the past that used textbooks. She goes over things thoroughly and for the price it's very much worth it. I have had many quarters of formal calculus and differential equations courses and I am kind of anxious to look to see what her approach to calculus is. I can't really answer how this class would be for a novice or someone who has not had linear algebra the past, but I really don't think they need to worry about that. Her method I feel will make a novice be successful and to understand the material. She is very easy to understand. Gives good examples but doesn't beat a dead horse either. What I like about her introductory remarks is that she says what linear algebra is all about and she points out what the core of the linear algebra is about and what you need to know. Having taken it before I would have to agree and she is dead on spot.

RCJK03-07-25 - ID, United States

I had to take Calculus I and II as accelerated classes while working full time. It was my first time taking this courses and was very overwhelming. Calcworkshop really made learning the subjects easier for me by having all the subjects easy to find and easy to understand explanations. I received a B in both classes which I am extremely happy with doing the classes in double time.

Jacqueline S.03-07-25 - SC, United States

Jenn is awesome!Her breakdown of the topic is beyond what you would expect. She is showing you how to arrive at the answer instead of doing a simple equation. Most people need to know the why it give confidence and structure to the learning process. This is what Jenn is great at, she knows how to deliver the information to a non math mind in a way that instills knowledge that you can forever draw from as you move forward. It's really well thought out. She is a true master teacher. Thanks for all that you do for us! Hugs n Blessings... JS

Rose M.03-07-25 - CA, United States

Best instructor ever, I have never had Math explained in a way that was so interesting. Her lectures and instruction is explained perfectly, and I will continue to use this for all my future math courses.

A Reviewer03-07-25 - United States

I needed help with college precalculus, they provided more than enough help that allowed me to succeed and get the scores I needed.

Jujuana03-05-25 - MO, United States

I love the videos the way each lesson is explained step by step. I love that she has examples that you can go over again and again in order to understand the way algebra works. I was lost because my instructor was flying through each lesson and I was totally lost. I attached my syllabus and they helped me stay focus on what I was working and give me a guide to go back and refresh what I went over in class.

Stacey01-31-25 - AZ, United States

Hello, I highly recommend getting a subscription to Jenn and her Calcworkshop teaching math service. I did a general, "go from bad to good at math", Google search and found out about Calcworkshop through responses to the topic on reddit. I've just started watching her videos and found them to be extremely helpful. I'm going back to college after a long absence and math was never my strong suit. So I'm starting at the very bottom of her available subjects and going from there. Just watching a couple of the videos has taken me from being dragged along not understanding to following along just fine in my math class. I'm moving from the "I'll never get this", to the "I look forward to understanding this", mindset in approaching math. This for me is huge, and even though I have a long way to go, I'm confident I will get there thanks to Jenn. Totally worth it!

Kathy W.01-14-25 - WA, United States

Calcworkshop is an outstanding source to learn math and understanding math concepts. Jenn is an outstanding master teacher. Every lesson is clearly presented making understanding easy to grasp. Practice lessons with accompanying answers are given for each section. I am 82, a retired teacher and lifelong learner. Learning calculus has always been on my bucket list. Calcworkshop is helping me reach my goal.

Cheryl01-14-25 - NY, United States

Calc workshop is the absolutely best resource for math and I have seen almost everything that exists out there. I have even recommended it to my daughter's school so that all the kids could use the videos during the summer months for the subject they plan to study in the fall. They are guaranteed to get a A if they have watched the videos and completed the problems before taking the class. Students who are weak in areas can access lower level classes and those who seek to advance above grade level can do so. The videos and exercises are crystal clear and the excellent presentations raise the bar for teachers everywhere. I have always believed that one great math teacher is important in the education process. The videos, exercises and problems are excellent. It is not possible to have ANY knowledge gaps. I have never seen anything on the market that even begins to compete with it!

Justin N.12-22-24 - OK, United States

Calculus can be a scary subject. I know I was scared. I had been out of any math class for over 23 years. I had taken an 8 week Calculus 1 class and felt like I was overloaded. Going into Calculus 2 I found CALCWORKSHOP.com. I used the training videos and material to really dive back into Calc 1 and prepare for Calc 2. Long story short with the material provided and ample study time, I finished Calc 2 with a 95%. Thanks Jenn!

Shelby12-10-24 - OH, United States

CalcWorkshop was a wonderful resource as someone going onto a college calculus 1 class after not having taken a math course in a year! Jenn always explained things in a logical order that built upon previous lessons, and the way she explained topics was always easy to understand. Calcworkshop saved this semester for me, and I couldn't be more grateful to have found this site. :)

Jordan Q.12-09-24 - AR, United States

Anyone struggling with math at any level would greatly benefit from this product. I signed up for it immediately after getting a D on my first exam in calculus 2 and ended up getting A's and B's on the remaining exams, getting a B overall in the class. Jenn breaks down the topics, without skipping any steps, in a way that makes them very easy to understand. I highly recommend this product!

N8Booker11-28-24 - MA, United States

I'm in school to get my degree Networking and Cybersecurity and I'm in my first year. I've been away from school for quite a long time so the concepts that are being taught although not foreign to me, have so much dust on them from a lack of being used in real world applications regularly.I stumbled upon CalcWorkshop by pure chance and it has been a game changer for me. Jen filled in the gaps in between what my Professor is teaching at a rapid fire pace and where my brain grasps and applies it. If not for Jen's approach, I'd have failed my test I took miserably!Am I grateful? It goes beyond words and not I recommend her workshops to everyone!

Kevin S.10-30-24 - CO, United States

Richard10-29-24 - Norway

RobWP10-26-24 - United States

RCJK03-07-25 - ID, United States

Jacqueline S.03-07-25 - SC, United States

Jujuana03-05-25 - MO, United States

See more reviews on Shopper Approved