Divergence Theorem (Defined w/ Step-by-Step Examples!)

Did you know that we can see the divergence theorem at work in some of our tastiest desserts?

Jenn (B.S., M.Ed.) of Calcworkshop® teaching divergence theorem

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

Imagine making a light and airy cream puff or éclair for dessert. The pate a choux dough is baked to perfection and is ready to be filled with some yummy pastry cream.

But let’s assume that the cream puff is rigid and does not expand when filled with cream.

What will happen?

Some of the pastry cream will eventually leak out of the puff.

And this is the idea behind the divergence theorem!

Divergence Theorem

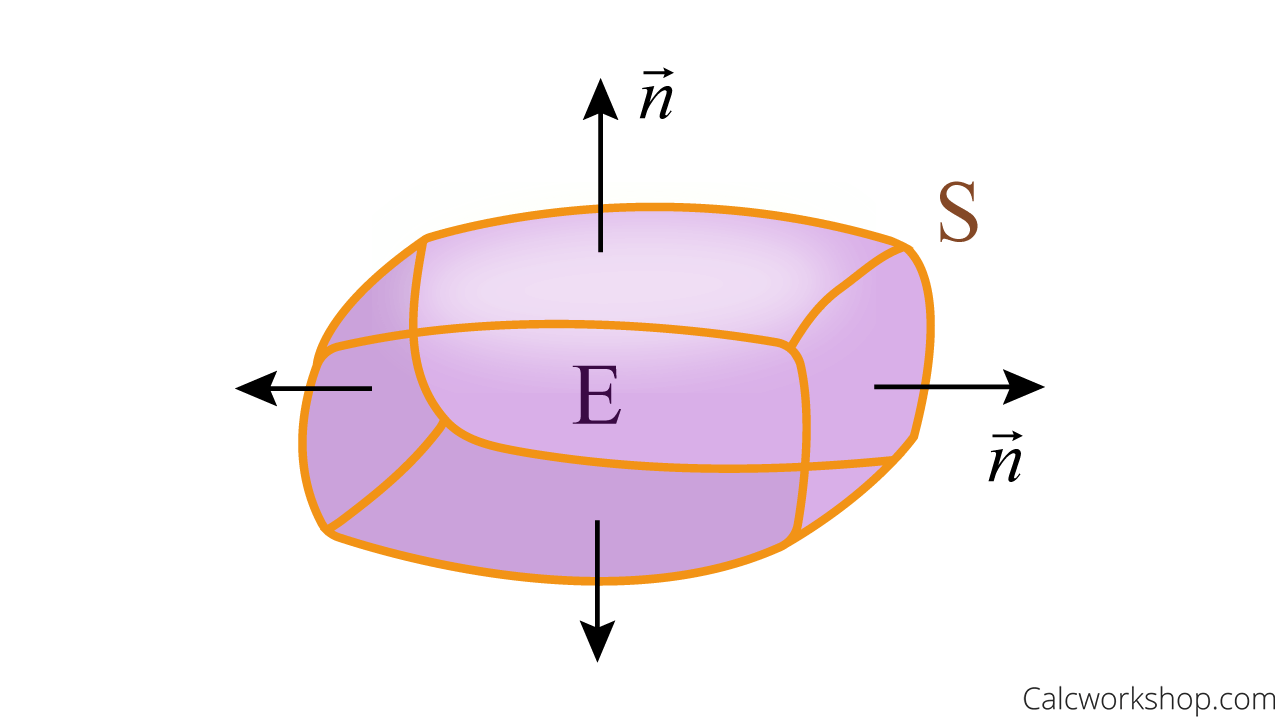
Simply stated, the divergence theorem, also called Gauss’ theorem, states that the total expansion of a fluid or gas (or pastry cream) inside a closed surface is equal to the fluid escaping the closed surface.

Remember, a vector field $\vec{F}$ represents the flux (flow) of a fluid, and the divergence of $\vec{F}$ is the gathering (sink) or dispersing (source) of the fluid inside some region.

This means we can turn our surface integral (flux integral) into a triple integral over the volume enclosed by the surface.

Formula

Let $E$ be a simple solid region and let $S$ be the boundary surface of $E$ , with a positive outward orientation. And let $\vec{F}$ be a vector field whose component functions have continuous partial derivatives on an open region that contains $E$ . Then

$\iint_{S} \vec{F} \cdot d \vec{S} = ∭_{E} div \vec{F} d V$

Divergence Theorem Geometric Interpretation

Therefore, that divergence theorem represents the net rate of outward flux per unit volume and plays a significant importance to the field of mathematics and engineering, in particular, electrostatics and fluid dynamics.

Cool!

Also, it’s important to note that if there is net flow “out of” the closed surface (i.e., $d i v \vec{F} > 0$ ), the integral is positive. Thus, if there is a net flow “into” the closed surface (i.e., $d i v \vec{F} < 0$ ), the integral is negative, just as we would expect.

Example

Let’s look at an example.

Evaluate the surface integral using the divergence theorem $∭_{D} div \vec{F} d V$ if $\vec{F} (x, y, z) = ⟨ x, y, z - 1 ⟩$ where $D$ is the region bounded by the hemisphere $0 \leq z \leq \sqrt{16 - x^{2} - y^{2}}$ .

First, we will calculate $d i v \vec{F} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}$ .

$div \vec{F} = \frac{\partial}{\partial x} [x] + \frac{\partial}{\partial y} [y] + \frac{\partial}{\partial z} [z - 1] = 1 + 1 + 1 = 3$

Next, we will find our limit bounds. Because we are told that a hemisphere bounds our region, we should use spherical coordinates.

Bounded Region Hemisphere

$\begin{aligned} 0 \leq z \leq \sqrt{16 - x^{2} - y^{2}} \\ 0 \leq z^{2} \leq 16 - x^{2} - y^{2} \\ 0 \leq \underset{ρ^{2}}{\underset{⏟}{x^{2} + y^{2} + z^{2}}} \leq 16 \\ 0 \leq ρ^{2} \leq 16 \\ 0 \leq ρ \leq 4 \end{aligned}$

And since $D$ is a hemisphere is has $360^{\circ}$ rotation around the xy-plane such that $0 \leq θ \leq 2 π$ , and the angle from the top of the hemisphere (positive z-axis) to the bottom of the plane is $90^{\circ}$ we know that $0 \leq ϕ \leq \frac{π}{2}$

Now we’re ready to evaluate our triple integral knowing that $d i v \vec{F} = 3$ , $0 \leq ρ \leq 4$ , $0 \leq θ \leq 2 π$ , and $0 \leq ϕ \leq \frac{π}{2}$ . And we must not forget the Jacobian determinate, $ρ^{2} \sin ϕ$ , for spherical coordinates!

$∭_{D} div \vec{F} d V = \int_{0}^{\frac{π}{2}} \int_{0}^{2 π} \int_{0}^{4} (3) (p^{2} \sin ϕ) d ρ d θ d ϕ = 256 π$

Easy, right!

Recap

So, let’s quickly recap some important concepts about Gauss’s divergence theorem.

The divergence theorem tells us that the flux of $\vec{F}$ across a surface is found by integrating the divergence of $\vec{F}$ over the region enclosed by the surface.
The divergence theorem equates a surface integral across a closed surface $S$ to a triple integral over the solid enclosed by $S$ .
The divergence theorem is a higher dimensional version of the flux form of Green’s theorem.

Nice.

And I bet the next time you shake a can of soda, pump air into a basketball or eat an éclair, cream puff, or jelly-filled donut, you’ll think of divergence theorem and smile!

Alright, let’s dive right into our lesson.

Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Divergence-Theorem-Example

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.

4.9 / 5

1,130 Reviews

Kevin S.10-30-24 - CO, United States

I had never even heard of discrete math before I had to take it for my Bachelor's in Cybersecurity. I had actually hoped that my math days were done! I suffered through class not understanding any of the presentations until I stumbled across Calcworkshop. I used the Calcworkshop lessons more than I used my instructor's lectures and my book. I ended up with a high B (just 12 points away from an A) thanks to Jenn. Without her easy to understand style of teaching, I'm not sure I would have even passed the class. Thank you so much!!!

Richard10-29-24 - Norway

Very well structured and site. It is well structured giving a good overview of the different topics regarding all mathematics where you easily can choose which path is applicable to your specific needs.The video lectures are superb with introduction to the topic followed by a detailed theoretically explaination and what I personally get most out of is; heaps of examples where you are taken and shown, step by step, the prosess of solving the problem. They also includd practice sheets and solutions to test yourself after each chapter. There is a lot to undertake on this site, but it provides an easy and understandable interface to map out what you need to do. The site has been very helpfull for me and I highly recommend it.

Maria03-26-25 - AB, Canada

I found Jenn's videos near the end of my discrete math class, so I only had a month to go through all of her discrete math lessons to study for my exam. I'm sure I would have aced it if I had more time but I got a pretty good grade considering I thought I would fail.So happy to be done that class!As advertised, Jenn is very thorough and doesn't skip steps, she lets you know exactly how she gets from a to b or she will refer you to other videos where she teaches the techniques she's using more in depth. This was extremely valuable to me, being a mature student taking advanced math while not remembering basic algebra.And it was fun to understand and solve complex problems vs memorize proof structures.

Robbin03-18-25 - CO, United States

Very well organized, helpful and comprehensive. It is great also to have access to prior course material so you can easily go back and refresh if you need to. Jenn is very clear and the number of examples leaves one comfortable with each topic. Couldn't be happier.

RCJK03-07-25 - ID, United States

I had to take Calculus I and II as accelerated classes while working full time. It was my first time taking this courses and was very overwhelming. Calcworkshop really made learning the subjects easier for me by having all the subjects easy to find and easy to understand explanations. I received a B in both classes which I am extremely happy with doing the classes in double time.

Jacqueline S.03-07-25 - SC, United States

Jenn is awesome!Her breakdown of the topic is beyond what you would expect. She is showing you how to arrive at the answer instead of doing a simple equation. Most people need to know the why it give confidence and structure to the learning process. This is what Jenn is great at, she knows how to deliver the information to a non math mind in a way that instills knowledge that you can forever draw from as you move forward. It's really well thought out. She is a true master teacher. Thanks for all that you do for us! Hugs n Blessings... JS

Rose M.03-07-25 - CA, United States

Best instructor ever, I have never had Math explained in a way that was so interesting. Her lectures and instruction is explained perfectly, and I will continue to use this for all my future math courses.

Jujuana03-05-25 - MO, United States

I love the videos the way each lesson is explained step by step. I love that she has examples that you can go over again and again in order to understand the way algebra works. I was lost because my instructor was flying through each lesson and I was totally lost. I attached my syllabus and they helped me stay focus on what I was working and give me a guide to go back and refresh what I went over in class.

Stacey01-31-25 - AZ, United States

Hello, I highly recommend getting a subscription to Jenn and her Calcworkshop teaching math service. I did a general, "go from bad to good at math", Google search and found out about Calcworkshop through responses to the topic on reddit. I've just started watching her videos and found them to be extremely helpful. I'm going back to college after a long absence and math was never my strong suit. So I'm starting at the very bottom of her available subjects and going from there. Just watching a couple of the videos has taken me from being dragged along not understanding to following along just fine in my math class. I'm moving from the "I'll never get this", to the "I look forward to understanding this", mindset in approaching math. This for me is huge, and even though I have a long way to go, I'm confident I will get there thanks to Jenn. Totally worth it!

Kathy W.01-14-25 - WA, United States

Calcworkshop is an outstanding source to learn math and understanding math concepts. Jenn is an outstanding master teacher. Every lesson is clearly presented making understanding easy to grasp. Practice lessons with accompanying answers are given for each section. I am 82, a retired teacher and lifelong learner. Learning calculus has always been on my bucket list. Calcworkshop is helping me reach my goal.

Cheryl01-14-25 - NY, United States

Calc workshop is the absolutely best resource for math and I have seen almost everything that exists out there. I have even recommended it to my daughter's school so that all the kids could use the videos during the summer months for the subject they plan to study in the fall. They are guaranteed to get a A if they have watched the videos and completed the problems before taking the class. Students who are weak in areas can access lower level classes and those who seek to advance above grade level can do so. The videos and exercises are crystal clear and the excellent presentations raise the bar for teachers everywhere. I have always believed that one great math teacher is important in the education process. The videos, exercises and problems are excellent. It is not possible to have ANY knowledge gaps. I have never seen anything on the market that even begins to compete with it!

Justin N.12-22-24 - OK, United States

Calculus can be a scary subject. I know I was scared. I had been out of any math class for over 23 years. I had taken an 8 week Calculus 1 class and felt like I was overloaded. Going into Calculus 2 I found CALCWORKSHOP.com. I used the training videos and material to really dive back into Calc 1 and prepare for Calc 2. Long story short with the material provided and ample study time, I finished Calc 2 with a 95%. Thanks Jenn!

Shelby12-10-24 - OH, United States

CalcWorkshop was a wonderful resource as someone going onto a college calculus 1 class after not having taken a math course in a year! Jenn always explained things in a logical order that built upon previous lessons, and the way she explained topics was always easy to understand. Calcworkshop saved this semester for me, and I couldn't be more grateful to have found this site. :)

Jordan Q.12-09-24 - AR, United States

Anyone struggling with math at any level would greatly benefit from this product. I signed up for it immediately after getting a D on my first exam in calculus 2 and ended up getting A's and B's on the remaining exams, getting a B overall in the class. Jenn breaks down the topics, without skipping any steps, in a way that makes them very easy to understand. I highly recommend this product!

N8Booker11-28-24 - MA, United States

I'm in school to get my degree Networking and Cybersecurity and I'm in my first year. I've been away from school for quite a long time so the concepts that are being taught although not foreign to me, have so much dust on them from a lack of being used in real world applications regularly.I stumbled upon CalcWorkshop by pure chance and it has been a game changer for me. Jen filled in the gaps in between what my Professor is teaching at a rapid fire pace and where my brain grasps and applies it. If not for Jen's approach, I'd have failed my test I took miserably!Am I grateful? It goes beyond words and not I recommend her workshops to everyone!

Kevin S.10-30-24 - CO, United States

Richard10-29-24 - Norway

Maria03-26-25 - AB, Canada

RCJK03-07-25 - ID, United States

Jacqueline S.03-07-25 - SC, United States

See more reviews on Shopper Approved