Did you know that when you solve a differential equation with a specific condition, you’re tackling an initial value problem?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In simpler terms, you’re looking for a solution that meets certain requirements to find a unique answer.
In a previous lesson, you learned about Ordinary Differential Equations. Now, you’ll dive deeper to explore n-parameter family of solutions and use an initial condition (IC) to figure out the constants in that family.
Understanding n-parameter Family of Solutions
So, what’s an n-parameter family?
Well, a first-order differential equation \(F\left(x, y, y^{\prime}\right)=0\) typically has a single arbitrary constant called a parameter \(\mathrm{c}\), whereas a second-order differential equation \(F\left(x, y, y^{\prime}, y^{\prime \prime}\right)=0\) usually has two arbitrary constants, denoted \(c_{1}\) and \(c_{2}\).

One Two Three Parameter — Solution Formulas
Therefore, a single differential equation can possess an infinite number of solutions corresponding to the unlimited number of choices for the parameters.
So, an n-parameter family of solutions of a given nth-order differential equation represents the set of all solutions of the equation. And we typically refer to an \(n\)-parameter family of solutions as the general solution – it’s easier to say!
Consequently, if we assign arbitrary constants to the differential equation, referred to as initial conditions, our general solution is called a particular solution because it represents a specific answer for some particular constraint.
It should also be noted that solutions of an \(\mathrm{n}\)-th order differential equation that are not included in the general solution are called singular solutions.
Example: Verifying and Finding Solutions to Initial Value Problems
Let’s look at an example of how we will verify and find a solution to an initial value problem given an ordinary differential equation.
Verify that the function \(y=c_{1} e^{2 x}+c_{2} e^{-2 x}\) is a solution of the differential equation \(y^{\prime \prime}-4 y=0\).
Then find a solution of the second-order IVP consisting of the differential equation that satisfies the initial conditions \(y(0)=1\) and \(y^{\prime}(0)=2\).
First, we will verify that the function is a solution by noticing that we are given a two-parameter family of solutions because we have a second-order differential equation. Therefore, we need to find the second derivative of our function.
\begin{align*}
\begin{aligned}
& y=c_{1} e^{2 x}+c_{2} e^{-2 x} \\
& y^{\prime}=2 c_{1} e^{2 x}-2 c_{2} e^{-2 x} \\
& y^{\prime \prime}=4 c_{1} e^{2 x}+4 c_{2} e^{-2 x}
\end{aligned}
\end{align*}
Now, we will substitute our derivatives into the ODE and verify that the left-hand side equals the right-hand side.
\begin{equation}
\begin{aligned}
& y^{\prime \prime}-4 y=0 \\
& \left(4 c_1 e^{2 x}+4 c_2 e^{-2 x}\right)-4\left(c_1 e^{2 x}+c_2 e^{-2 x}\right)=0 \\
& 4 c_1 e^{2 x}+4 c_2 e^{-2 x}-4 c_1 e^{2 x}-4 c_2 e^{-2 x}=0 \\
& 0=0
\end{aligned}
\end{equation}
Now, we will find a solution to the second-order IVP by substituting the initial conditions into their corresponding functions.
\begin{equation}
\text { If } y=c_1 e^{2 x}+c_2 e^{-2 x} \text { and } y(0)=1, \text { then }
\end{equation}
\begin{align*}
1=c_{1} e^{2(0)}+c_{2} e^{-2(0)} \Rightarrow 1=c_{1}(1)+c_{2}(1) \Rightarrow 1=c_{1}+c_{2}
\end{align*}
\begin{equation}
\text { If } y^{\prime}=2 c_1 e^{2 x}-2 c_2 e^{-2 x} \text { and } y^{\prime}(0)=2 \text {, then }
\end{equation}
\begin{align*}
2=2 c_{1} e^{2(0)}-2 c_{2} e^{-2(0)} \Rightarrow 2=2 c_{1}(1)-2(1) \Rightarrow 2=2 c_{1}-2 c_{2}
\end{align*}
Next, we will solve the resulting system for \(c_{1}\) and \(c_{2}\).
\begin{align*}
\left\{\begin{array} { c }
{ 1 = c _ { 1 } + c _ { 2 } } \\
{ 2 = 2 c _ { 1 } – 2 c _ { 2 } }
\end{array} \Rightarrow \left\{\begin{array}{c}
c_{1}+c_{2}=1 \\
c_{1}-c_{2}=1
\end{array} \Rightarrow c_{1}=1 \quad \text { and } \quad c_{2}=0\right.\right.
\end{align*}
Therefore, the particular solution for the IVP given the initial condition is:
\begin{equation}
\begin{aligned}
& y=(1) e^{2 x}+(0) e^{-2 x} \\
& y=e^{2 x}
\end{aligned}
\end{equation}
Awesome!
I find that it’s helpful to remember that Initial condition(s) are values of the solution and/or its derivative(s) at specific points. Which means, according to Paul’s Online Notes that solutions to “nice enough” differential equations are unique; hence, only one solution will meet the given conditions.
The Game-Changing Existence and Uniqueness Theorem
But how do we know there will be a solution to the differential equation?
The Existence of a Unique Solution Theorem is a key concept in this course. It provides specific conditions that ensure a unique solution exists for an Initial Value Problem (IVP).
Definition: The existence-unique solution theorem says that if we let \(\mathrm{R}\) be a rectangular region in the \(x y-\) plane defined by \(a \leq x \leq b, c \leq y \leq d\) that contains the point \(\left(x_{0}, y_{0}\right)\) in its interior. And if \(f(x, y)\) and \(\frac{\partial f}{\partial y}\) are continuous on \(\mathrm{R}\), then there exists some interval \(\left(x_{0}-h, x_{0}+h\right), h>0\), contained in \([a, b]\), and a unique function \(y(x)\), defined on \(I_{0}\), that is a solution of the initial value problem.
That’s pretty “mathy” right?!
In *sorta* simpler terms, the existence-unique solution theorem essentially states that under specific conditions, there is a unique solution for an initial value problem. If a point (x₀, y₀) is within a rectangular region R in the xy-plane, and both the function f(x, y) and its partial derivative with respect to y are continuous in R, then there is an interval (x₀-h, x₀+h), with h>0, contained within the range [a, b]. Within this interval, a unique function y(x) exists as a solution to the initial value problem.
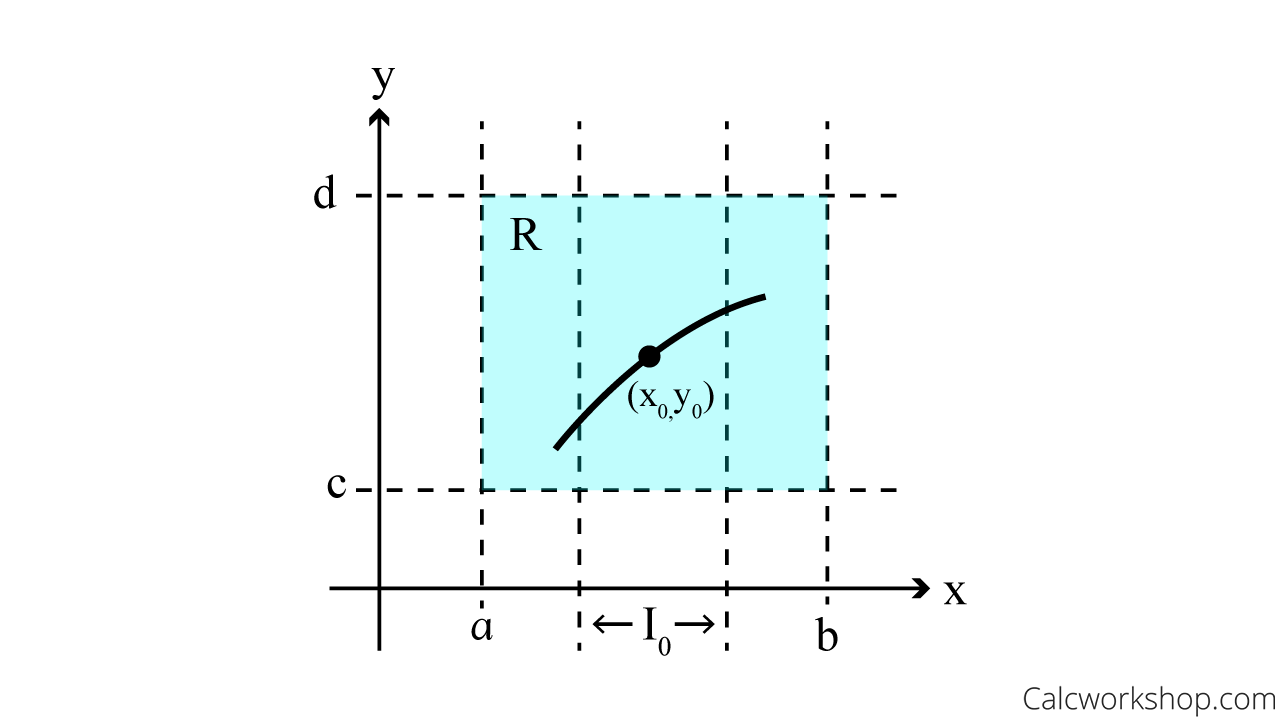
Existence Uniqueness Theorem — Graphical
Example: Solving an IVP with Given Initial Conditions
Let’s break this down into easy-to-understand steps by working an example.
Determine whether the existence-uniqueness theorem implies the given initial value problem has a unique solution through the given point.
\begin{equation}
y^{\prime}=y^{2 / 3},(8,4)
\end{equation}
First, we will verify that our ODE is continuous by letting \(f(x, y)=y^{\prime}\) and graphing the curve.
\begin{equation}
f(x, y)=y^{2 / 3}
\end{equation}

ODE — 3D Graph
So, \(f(x, y)\) is continuous for all real numbers.
Next, we will take the partial derivative with respect to \(\mathrm{y}\) and determine if the partial derivative is also continuous.
\begin{align*}
\frac{\partial f}{\partial y}=f_{y}=\frac{2}{3} y^{-1 / 3}=\frac{2}{3}\left(\frac{1}{\sqrt[3]{y}}\right)
\end{align*}
This indicates that a unique solution exists when \(y>0\).
Therefore, we can safely conclude that our given point \((8,4)\) will provide a unique solution because our \(y\)-value is greater than zero.
Perfect!
Going forward…
So, together we will dive into the world of n-th parameter family of solutions, find solutions for initial value problems, and determine the existence of a solution and whether a differential equation contains a unique solution through a given point.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.