What is the product rule?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Good question, and that’s what we’re covering in today’s calculus class.
Let’s jump to it!
The Product Rule
Simply put, the term “product” means two functions are being multiplied together.
Discovered by Gottfried Leibniz, this rule allows us to calculate derivatives that we don’t want (or can’t) multiply quickly.
In other words, the product rule allows us to find the derivative of two differentiable functions that are being multiplied together by combining our knowledge of both the power rule and the sum and difference rule for derivatives.
The first times the derivative of the second plus the second times the derivative of the first, as noted by Britannica.
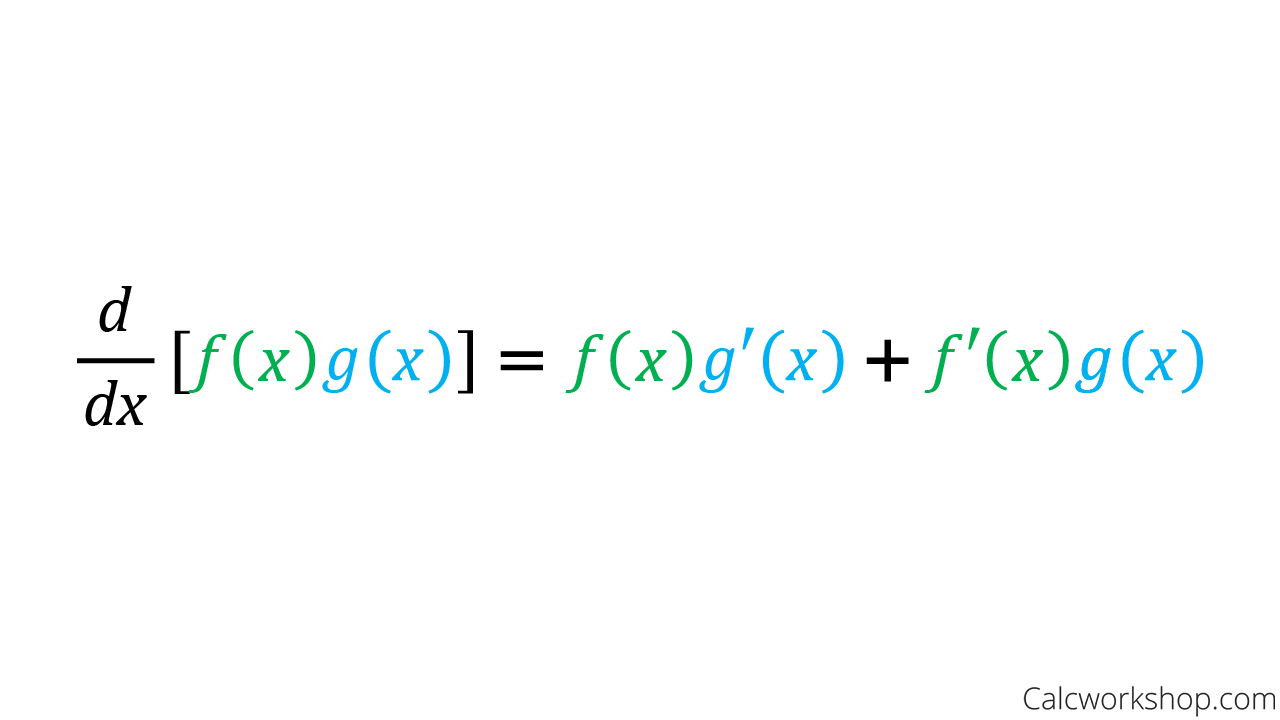
Product Rule Formula
To better understand this formula, let’s work through a few examples, using color-coding to make things easier to follow.
Worked Example
For instance, let’s find the following derivative.
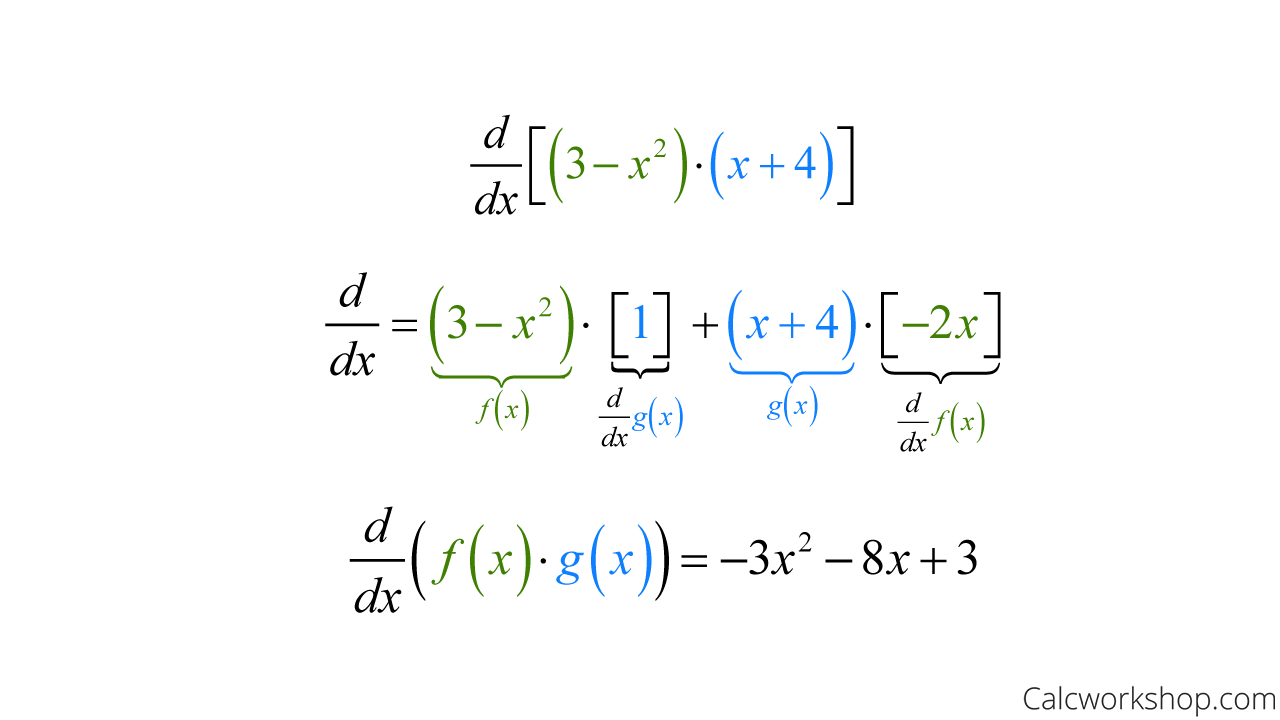
Derivative Product Rule Binomial
See, using the product rule is pretty easy!
Common Mistakes Using Product Rule
But I do want to caution you — the derivative of a product does not equal the product of derivatives.
Using the same two functions from above, let’s see this cautionary tale unfold:
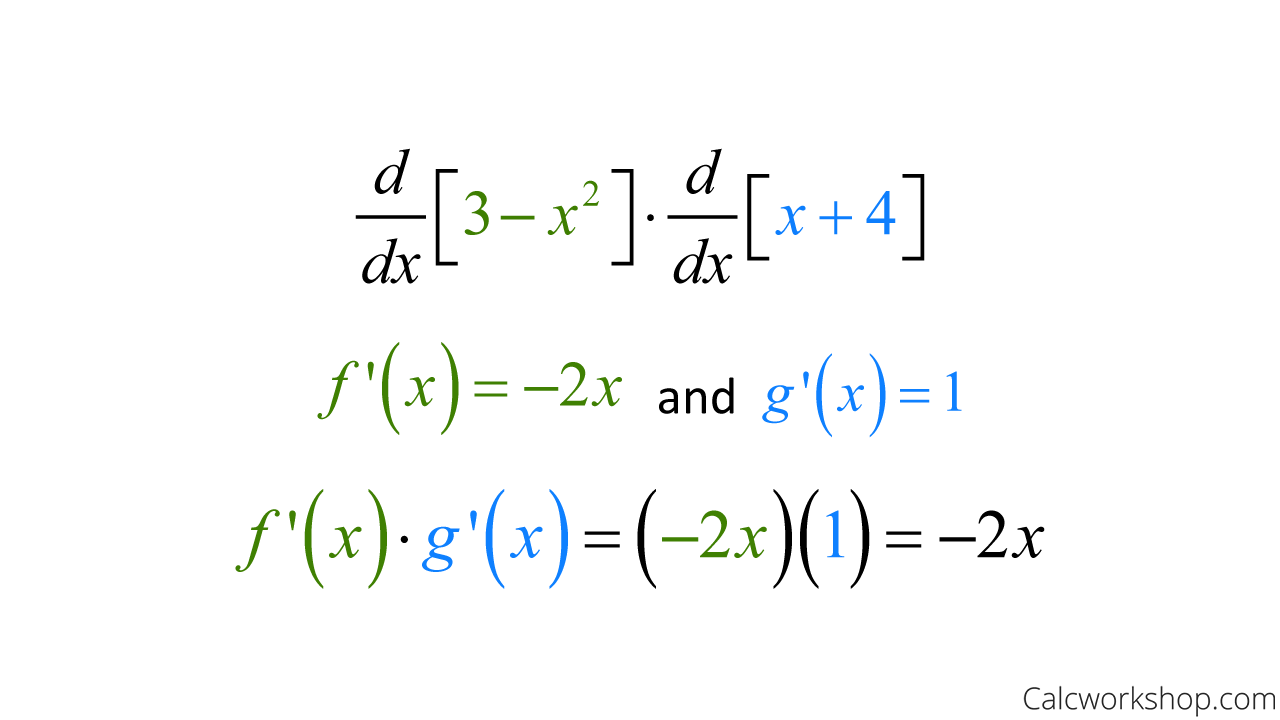
Product Of Two Derivatives
But as we can see, the derivative of the product is not the same as the product of derivatives as:
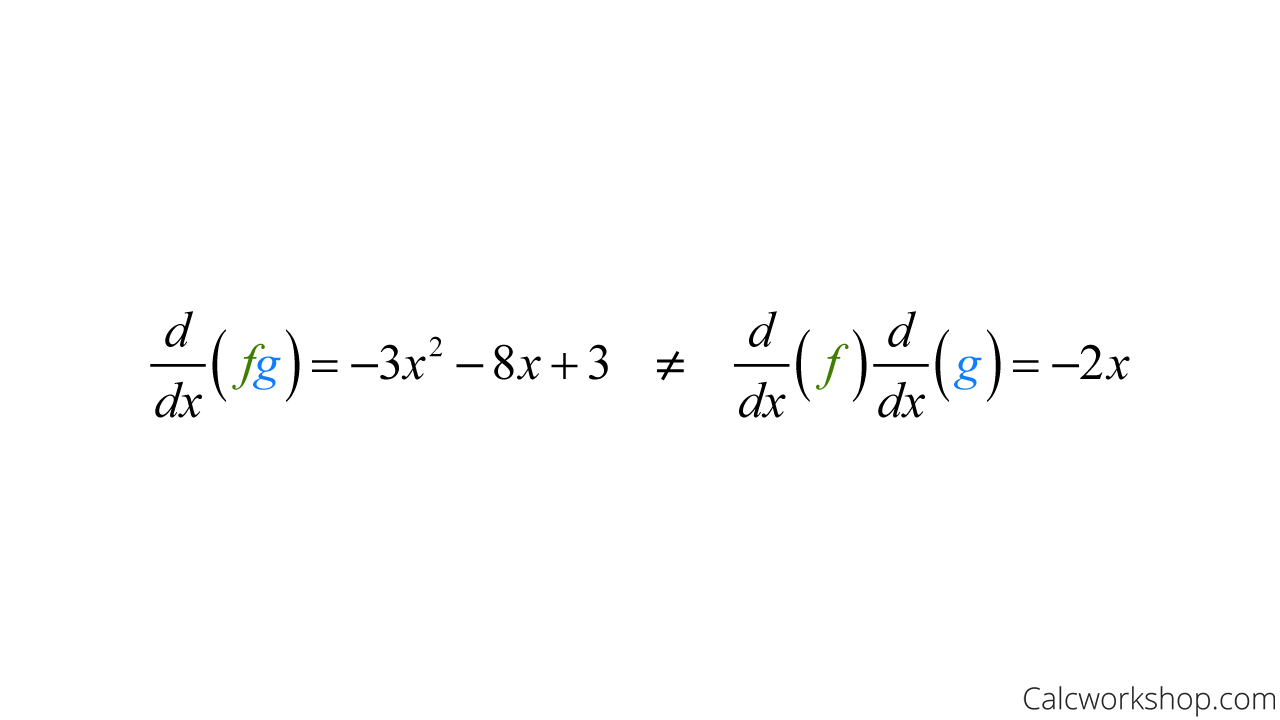
Derivative Of Product Does NOT Equal Product Of Derivative
This is a very common mistake that students make, but now that you know what “not to do,” you’re well on your way to success.
Ex) Instantaneous Rate Of Change
Okay, so let’s investigate two more examples.
Suppose we are asked to find the derivative of the h(x) when x = 1, as seen below.
First, we will need to use the product rule to calculate the derivative, and then we will plug in the value of 1 to find the instantaneous rate of change.
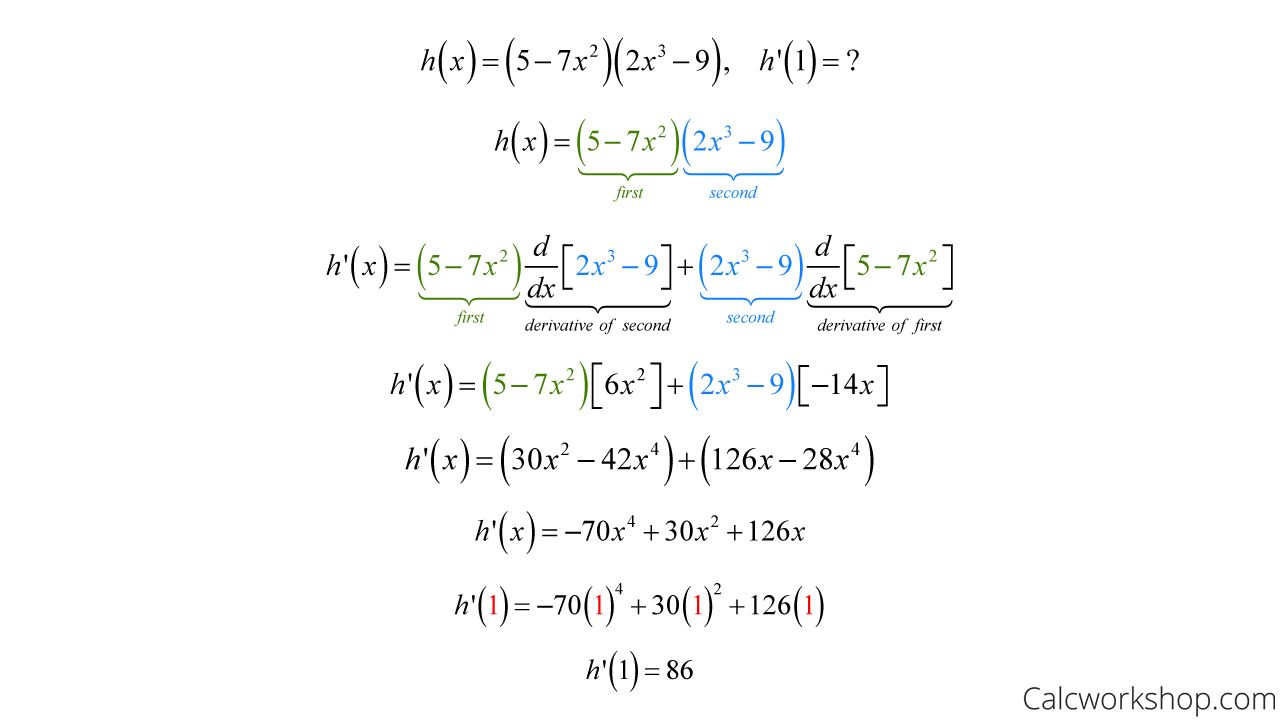
Use Product Rule To Find The Instantaneous Rate Of Change
So, all we did was rewrite the first function and multiply it by the derivative of the second and then add the product of the second function and the derivative of the first. And lastly, we found the derivative at the point x = 1 to be 86.
Now for the two previous examples, we had options for how to find the derivative:
- Simplify first, then use the power rule to find the derivative
- Or use the product rule and then simplify
Ex) Trig Functions
So, will there ever be a time when the product rule is the only option for computing the derivative?
Yes! In the following example, we must use the product rule to find the rate of change because we cannot simplify the expression any further as we are dealing with a product of two functions entirely unrelated.
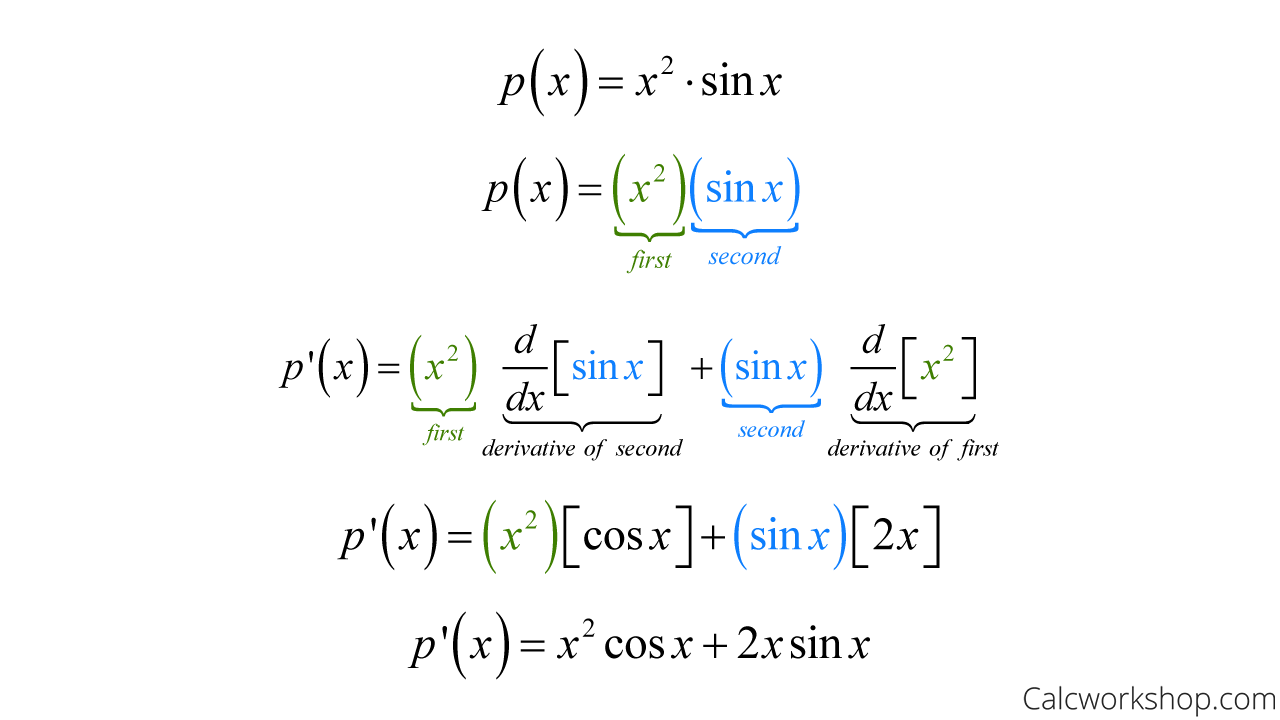
Product Rule Trig Functions
Note that we will learn how to find the derivative of trig functions in a future lesson. I merely wanted to demonstrate the “awesomeness” of this rule with this example and prove its usefulness.
Ex) More Than Two Functions
And did you know that we can extend this idea to the product of more than two functions?
For example, suppose we wanted to find the derivative of the product of three functions. You can use the following framework to accomplish this task.
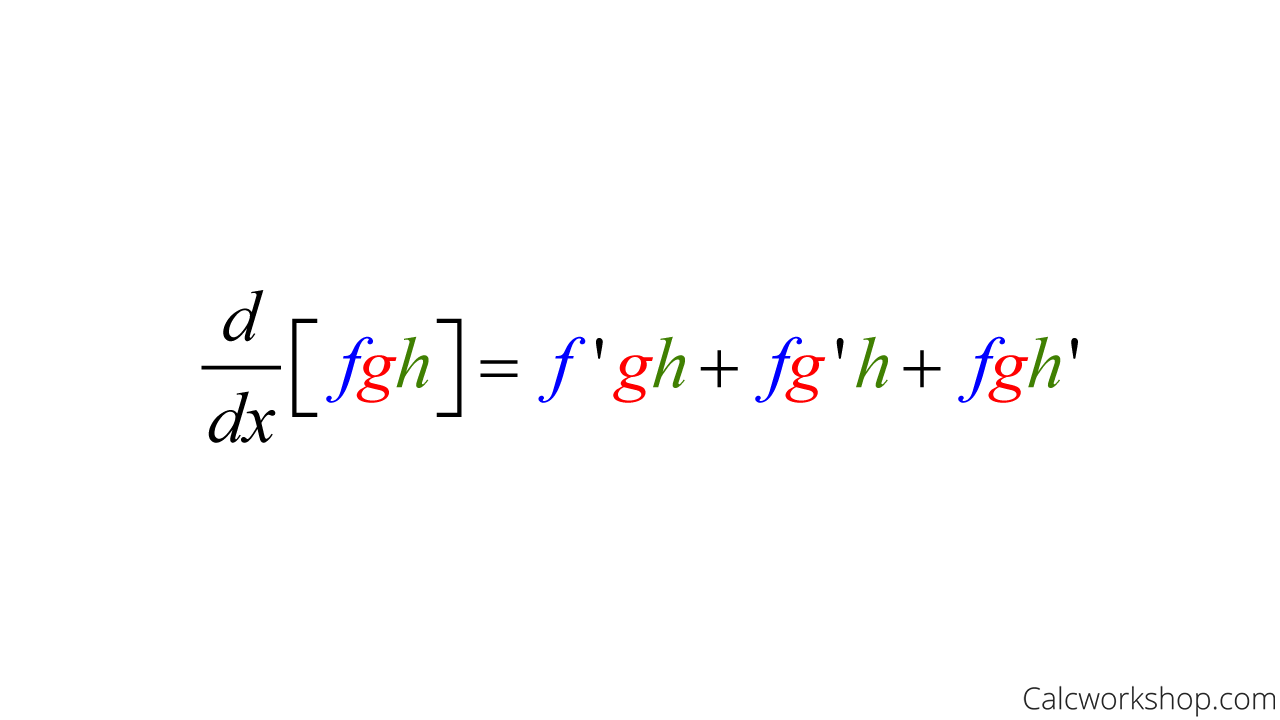
Product Rule For Three Functions
And it also works with more functions in a similar manner.
Together we will walk through countless examples of using the product rule and applying our algebra skills to simplify our results for differentiating problems where one function is multiplied by another.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.