Did you know that you already have a leg up in memorizing the six fundamental trig derivatives, all thanks to the Pythagorean Identity?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s true!
The properties you discovered in trigonometry when you learned about cofunctions, angles, and the Pythagorean Identity will help you make some pretty cool connections which makes memorizing these incredible differentiation rules much easier.
Below are the six trig derivatives. Take a look at them closely and see if you can spot any connections.
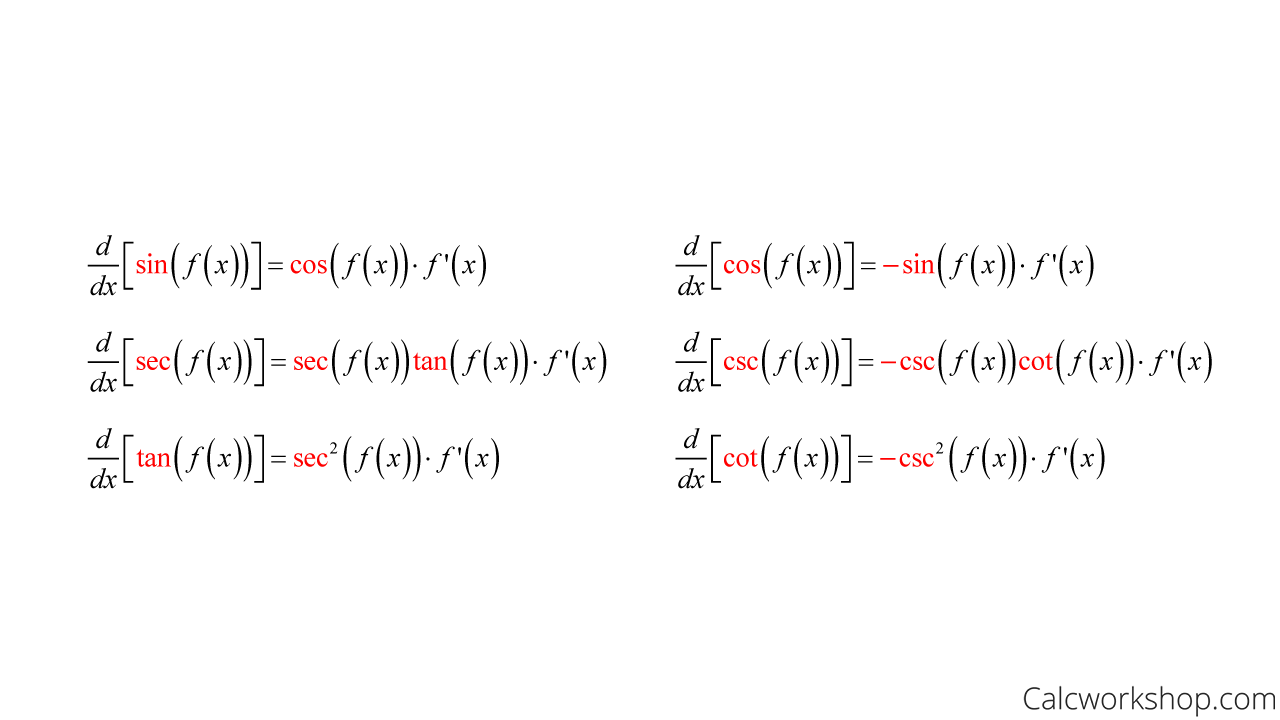
Derivatives Of Trig Functions
Proof
But before we get to their similarities, let’s start with a proof for a trigonometric derivative, so we can see how our limit definition of derivative paves the way for our ever-important formulas.
Let’s prove that the derivative of sin(x) is cos(x).
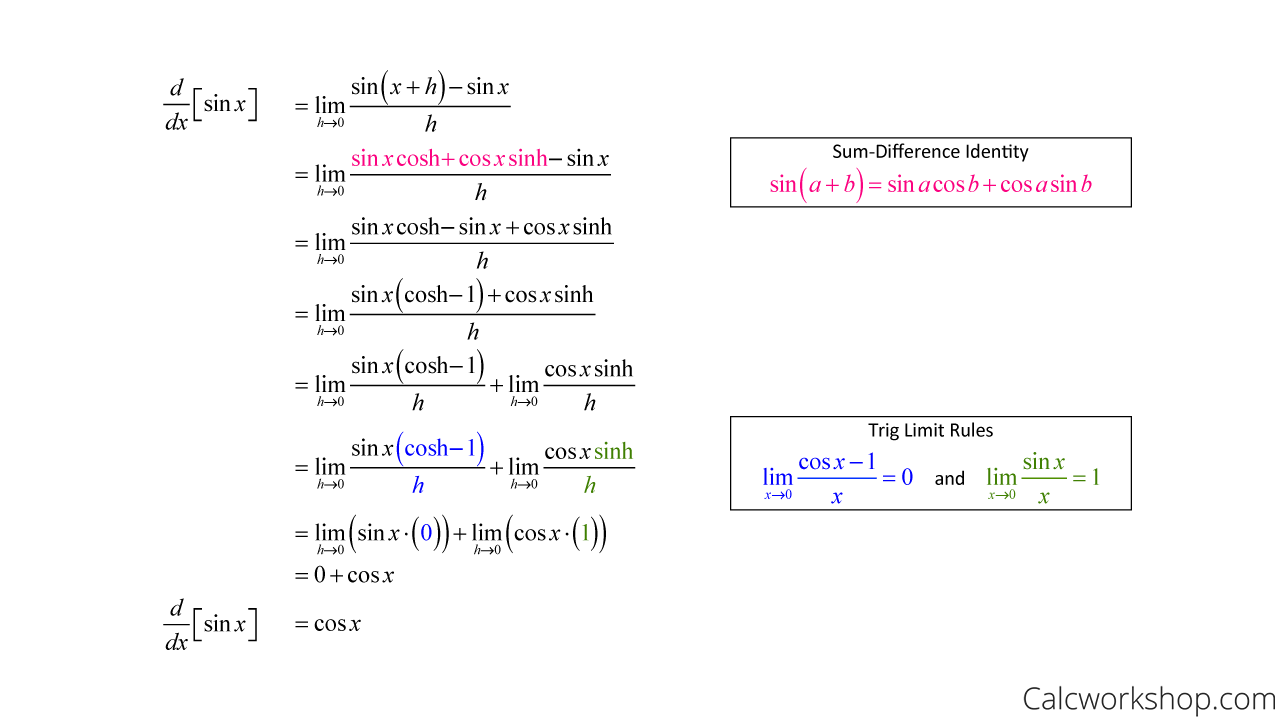
Proof That Derivative Of Sin Is Cos
Thankfully we don’t have to use the limit definition every time we wish to find the derivative of a trigonometric function — we can use the following formulas!
Notice that sine goes with cosine, secant goes with tangent, and all the “cos” (i.e., cosine, cosecant, and cotangent) are all negative.
And this shouldn’t surprise you too much, I hope, because the connections of how “sine and cosine” and “secant and tangent” go together were first established in your trig class when you learned about cofunctions and the Pythagorean Identity!
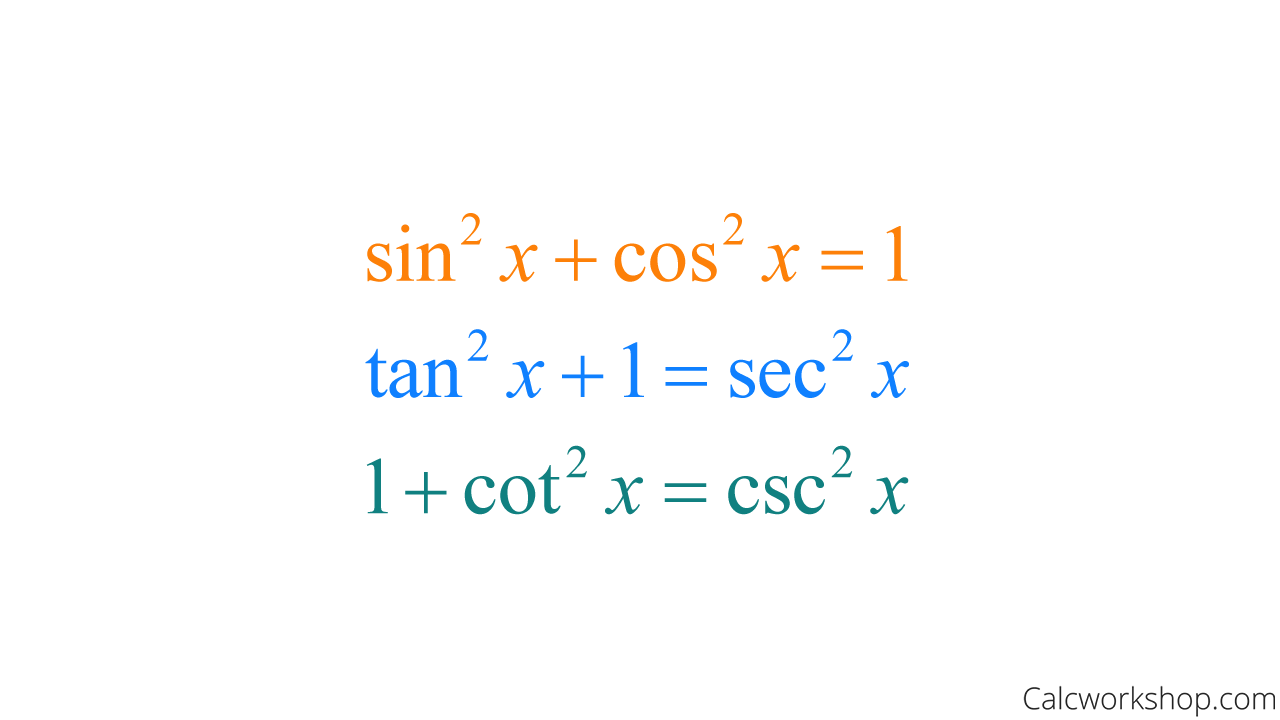
Pythagorean Identities
See, memorizing the formulas for trig derivatives is easy — because you already know what goes together!
Awesome!
How To Take Derivatives Of Trig Functions
But, getting the hang of trig derivatives can be confusing at first, even if you know what goes together, like sine and cosine.
The key to understanding trigonometric differentiation is to think of the chain rule, as trig functions have two layers:
- Trig
- Angle
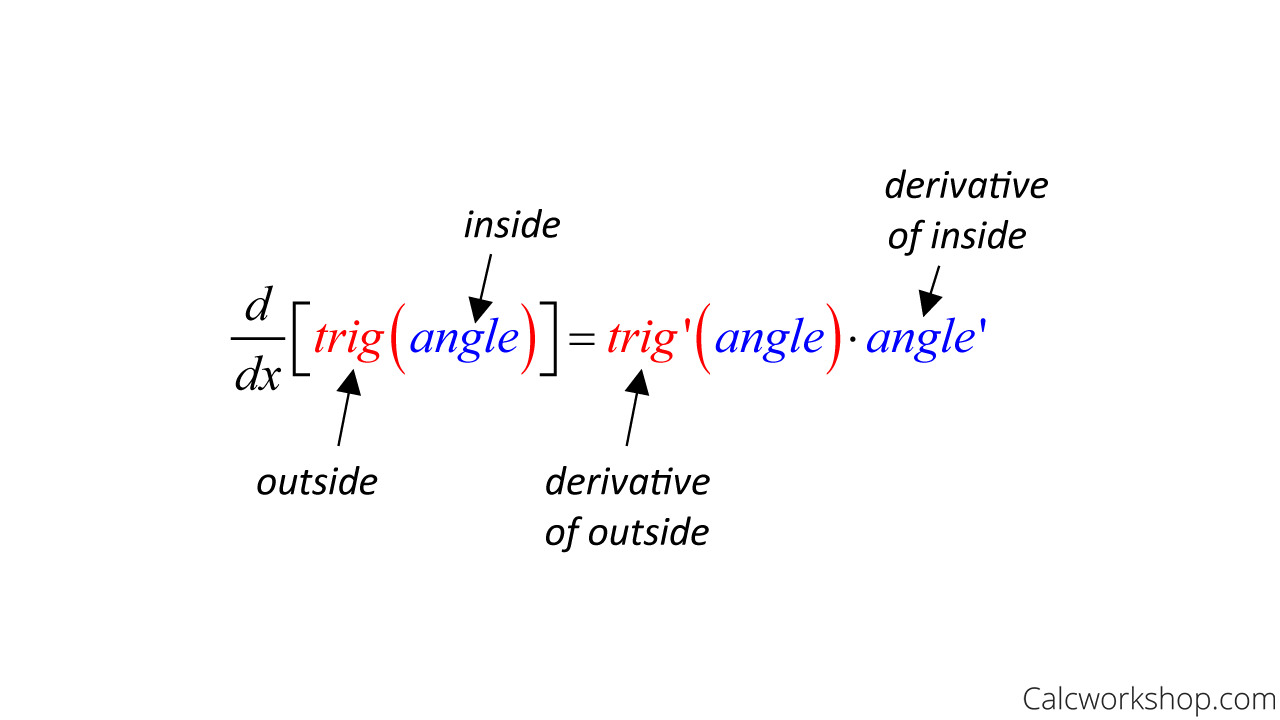
How To Find Derivative Of Trig Functions
This means that every time we take the derivative of a trig function, we are actually applying the chain rule by taking the derivative of the outside piece (trig) and then multiplying by the inside piece (angle).
Examples
Okay, so now let’s look at a few examples of putting these trig rules into action.
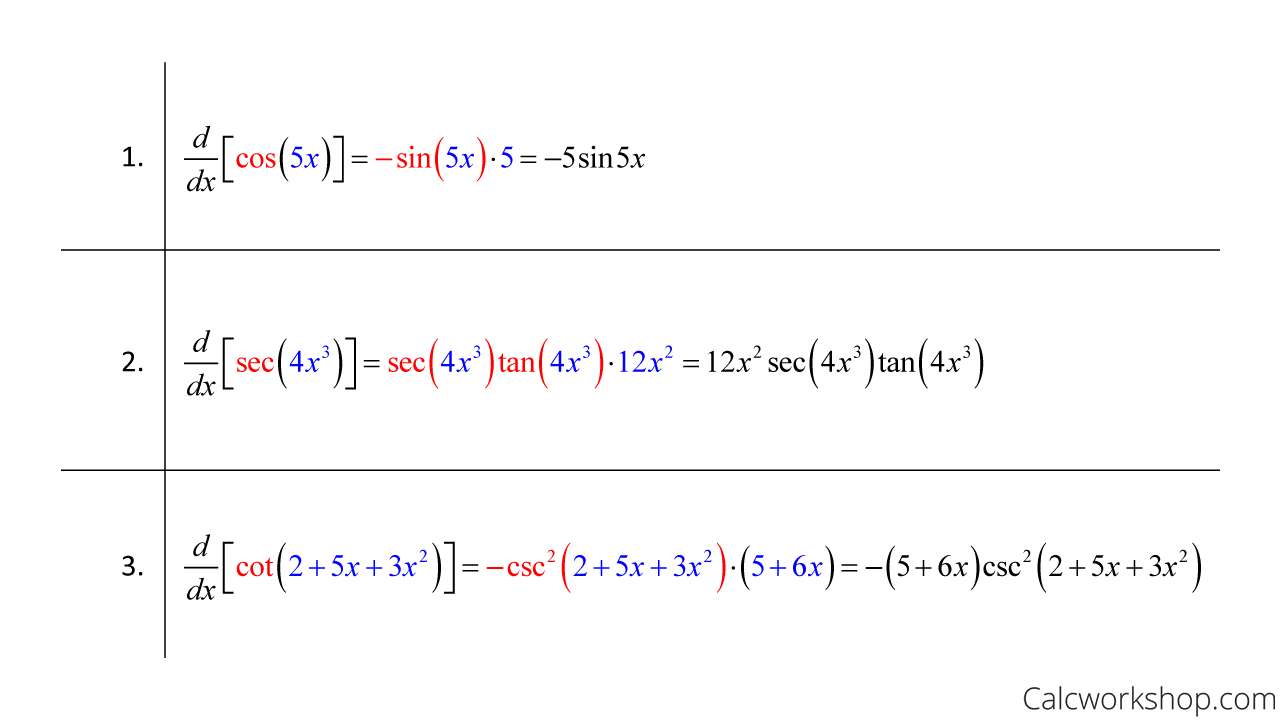
Trig Differentiation – Worked Out Examples
See, all we did was take the derivative of the trig portion, keeping the angle untouched, and then we multiplied by the derivative of the angle!
Summary
Together we will walk through 12 examples in detail and see how trig derivatives are easy to use and apply.
And here’s what even more tantalizing — knowing your derivatives for trigonometric functions will not only aid you in being able to answer homework questions successfully but will be instrumental in modeling situations in the real-world like motion, vibrations, waves, and more.
Cool, right?
Let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.