What is the definition of a derivative?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
That’s a good question, and that’s exactly what you’re going to learn about in today’s calculus class!
Let’s dive in!
Did you know that the geometric meaning of the word “derivative” is the slope of the tangent line of a curve at a point, which signifies the rate of change at a particular point?
But even more incredible is the fact that the concept of rate of change is one of the most foundational concepts in all of calculus, and it all begins with the definition of derivative.
This now brings us to two important questions:
- What do we mean by “rate of change?”
- How do we use the definition of derivative formula to find the slope of a function?
Backstory
Okay, so first, let’s recall from Algebra 1 how the slope of a straight line represents the change in y divided by the change in x. This means that the slope of a straight line has only one constant slope or rate of change.
Well, during the 17th century, both Isaac Newton and Gottfried Leibniz surmised that this concept of slope could be applied to curves (i.e., something that has a changing or variable rate of change). Thus, the method for calculating the derivative was born.
Defining The Slope
Here’s how this works and what Newton and Leibniz discovered.
Look at the graph below. Suppose we want to determine the slope of the curve at point P. This means we need to find the slope of the tangent line at point P.
Well, if we only know how to calculate the slope of a straight line, then let’s find another point on the curve and calculate the slope of the line between these two points!
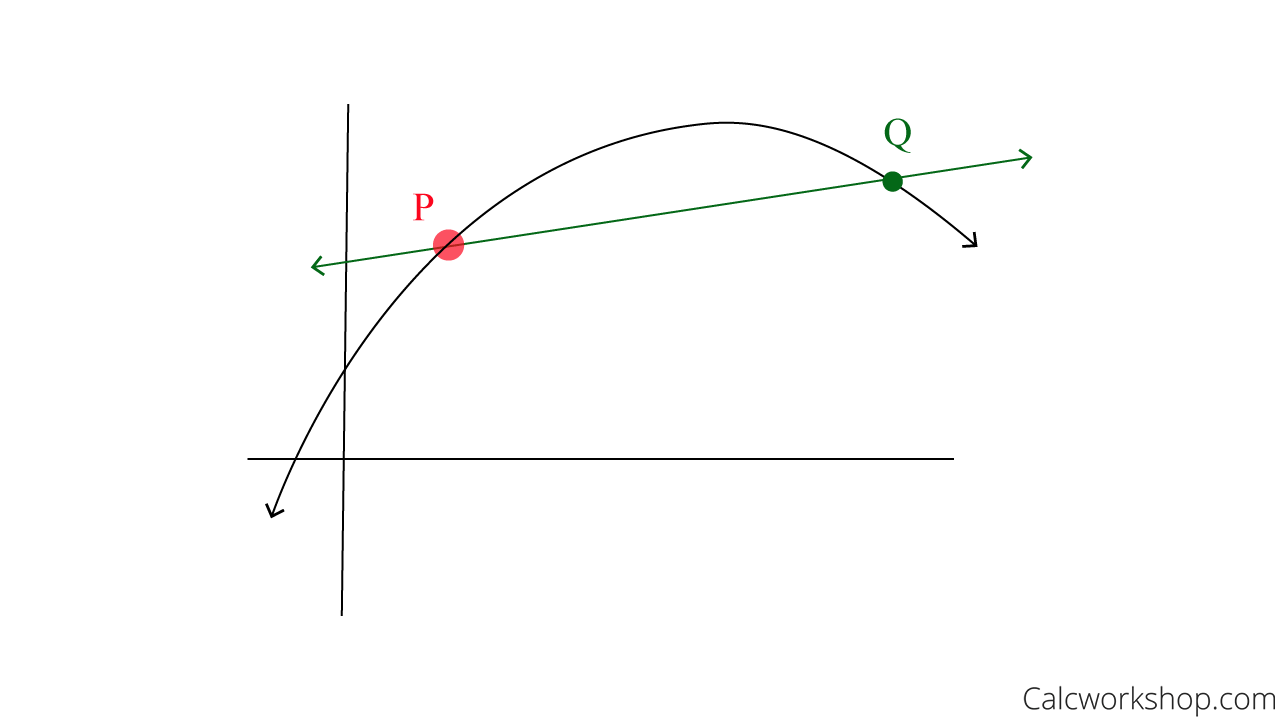
Slope Secant Line P To Q
But I think we would all agree that this green line between points P and Q doesn’t accurately represent the slope at point P only. So, what do we do? Let’s find another point, but this time let’s make sure it’s closer to P and recalculate.
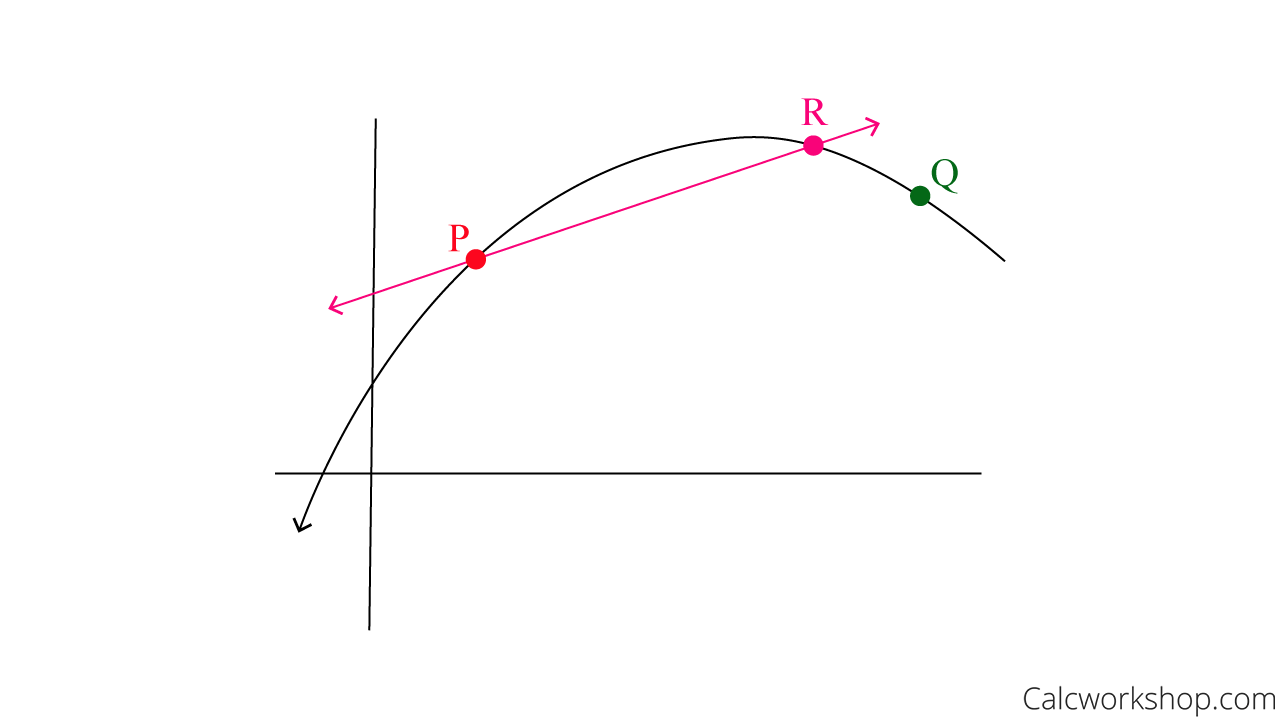
Slope Secant Line P To R
Alright, so the pink line between P and R is better, but it’s still not what we’re looking for. So, let’s try again, this time choosing a point even closer to point P.
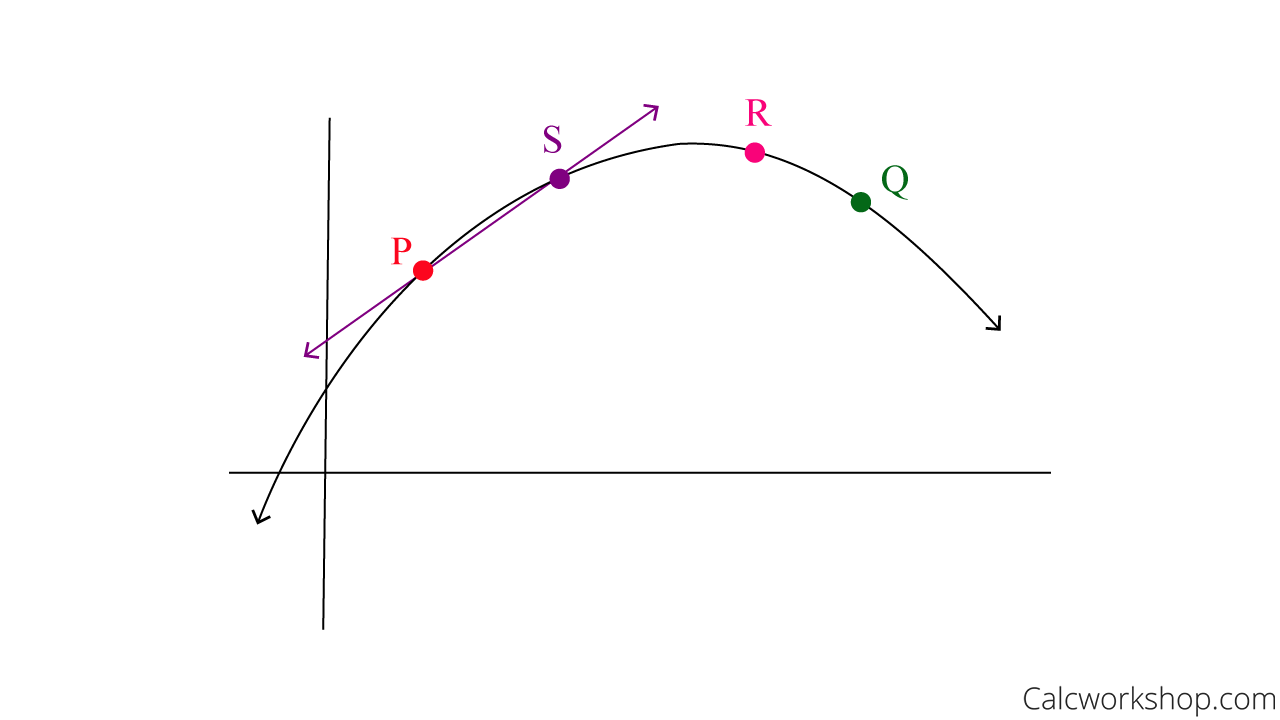
Slope Secant Line P To S
Alas, even the purple line from P to S still isn’t what we’re looking for, but we are beginning to realize something really critical.
As the distance between the two points gets smaller and smaller, the more accurate the slope of each secant line becomes.
But what we need is for the two points to be the same point — and we know from Algebra and Geometry that to find a line, we need two distinct points.
So, what do we do now?
Use Limits!
A limit means to approach, without actually touching a particular point, right? So, if we say that we are choosing another point whose distance from P is almost zero, then we can accurately calculate the slope at point P.
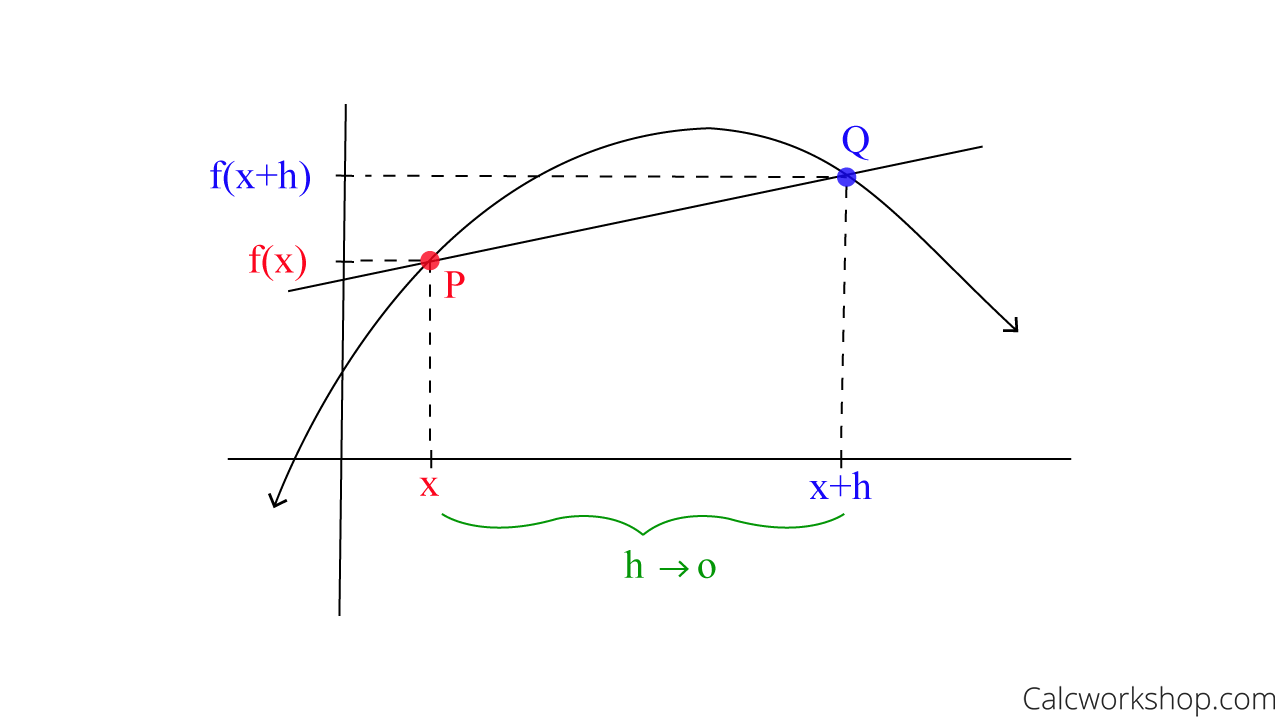
Limit Definition Derivative
Formulas & Notation
And if we take limit as h approaches zero the difference quotient becomes the definition of derivative, or limit definition of derivative, whose formula is represented as follows:

Definition Derivative Formula
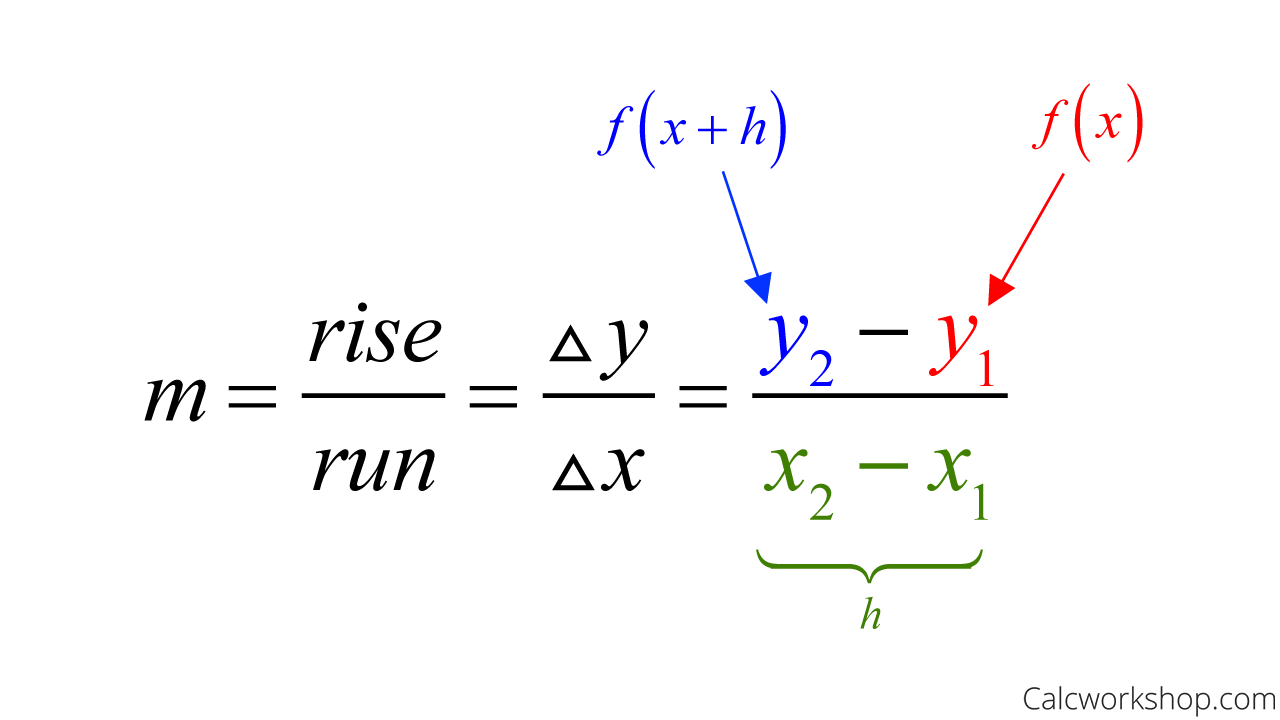
Slope Of Tangent Line – Formula
Cool, right?
We use the letter m to represent the slope of a straight line, and we use any of the following notations to represent the derivative (slope) of a curve:

Derivative Notation
Example – Using Definition Of Derivative
So, now let’s use this handy-dandy formula to find the rate of change, or as some textbooks or problems refer to it as the instantaneous rate of change as it allows us to calculate the slope of the line tangent at a particular point (i.e., one particular instance)
Use the definition of the derivative to find the slope of the tangent line.
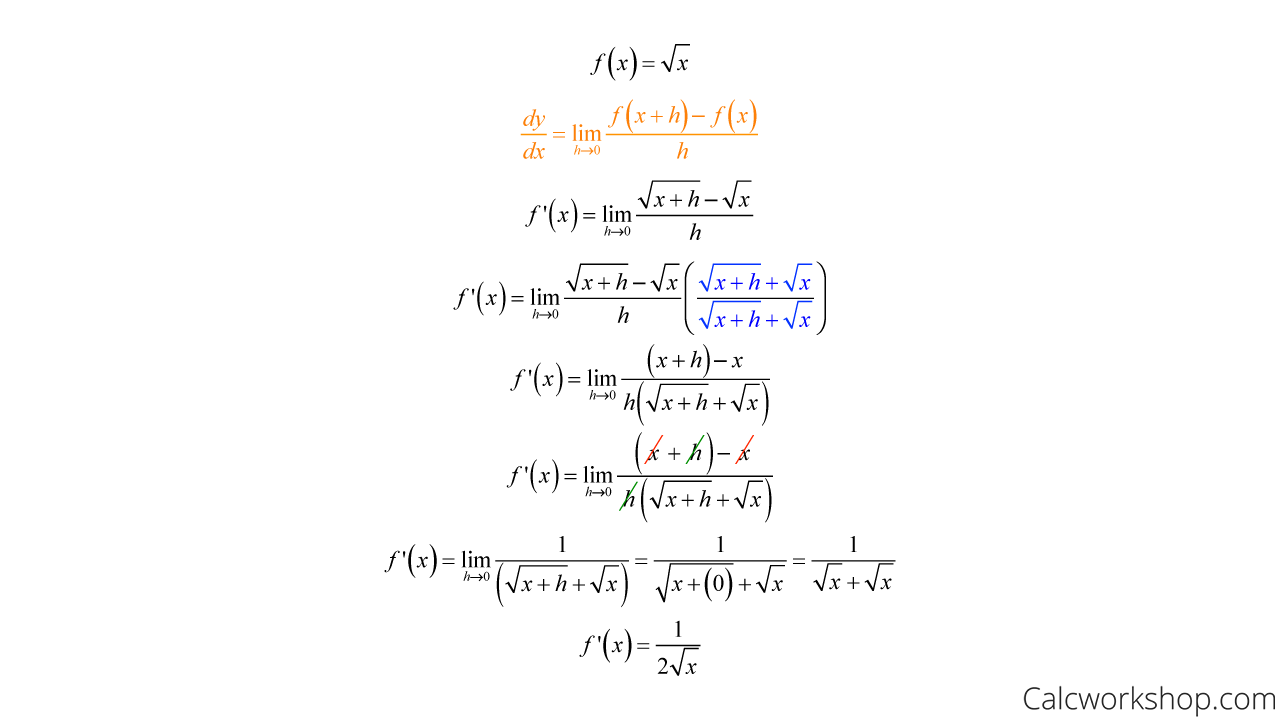
Definition Of The Derivative – Square Root Of X
Example – Using Limit Definition Of Derivative
Use the limit definition of the derivative to find the instantaneous rate of change for the function f(x) = 3x^2 + 5x + 7 when x = -2.
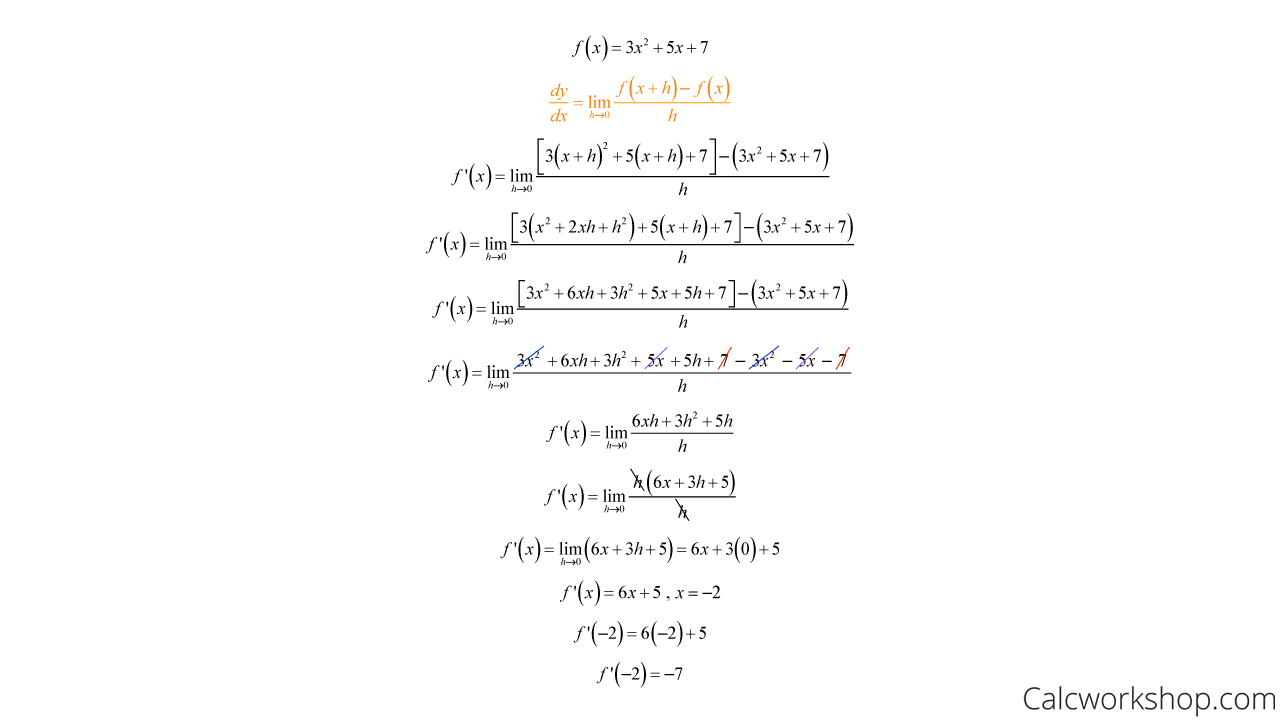
Instantaneous Rate Change – Example
And as Paul’s Online Notes nicely states, the definition of derivative not only helps us to compute the slope of a tangent line, but also the instantaneous rate of change of a function and the instantaneous velocity of an object which we will expand upon in future lessons.
Cool!
Summary
Throughout this lesson, you’ll learn about the limit definition of the derivative and its notation for finding the derivative of a curve for a general value of x (similar to the 1st example). In addition, you’ll understand how to solve for a specific value of x (similar to the 2nd example).
We will also look at an alternate version of the definition of derivative and methods for evaluating the limit definition for polynomials, root functions, and piecewise functions such as absolute value.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.