What is Rolle’s Theorem?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
And how is it useful?
All good questions that’ll be explained shortly in today’s lesson.
Let’s go!
Imagine you’re a detective and you are tracking a suspect. You know the precise moment the suspect left their house, and also when they returned home again, but you are curious as to what they did while away. What path did they take? Did they make any strange turns or stops along the way?
Oddly enough, Rolle’s Theorem can help us assemble the clues.
How?
Rolle’s theorem has a way of guaranteeing that there is a least one point (moment) within a closed interval (leaving and returning to the house) at which the derivative is zero (suspect makes a turn along their path).
Let’s learn how.
Defined w/ A Step-by-Step Process
Rolle’s Theorem states that if f is a continuous function on the closed interval [a,b], differentiable in the open interval (a,b), and f(a)=f(b) then there exists at least one number c in (a,b) such that the f’(c) = 0.
But what does this theorem really mean?
Let’s use our suspicious suspect to sort this out. Let a and b be our time, and f(a) and f(b) be the suspect’s house. So, the suspect leaves the house f(a) at time a and returns sometime later. This would be time t=b and since the suspect is returning to the same place they left, we know that f(a) is equal to f(b).
Now, if we can prove that our suspect stays on a continuous path while they are away from the house, then there will come a moment when the suspect must stop and turn (i.e., derivative equal to zero) in order to return home again.
And that’s all their is to Rolle’s Theorem. If we are given a closed interval where the y-values equal, and the path is continuous, then at some point within the interval the slope will be zero.
Rolle’s Theorem is a simple three-step process:
- Check to make sure the function is continuous and differentiable on the closed interval.
- Plug in both endpoints into the function to check they yield the same y-value.
- If yes, to both steps above, then this means we are guaranteed at least one point within the interval where the first derivative equals zero.
Worked Example
Let’s look at an example to see this in action.
Suppose we are asked to determine whether Rolle’s theorem can be applied to
Step 1:
Okay, so first, we will check to see that f(x) is a continuous and differentiable function on the interval.
Since
Step 2:
Now, we must verify that the y-values at the endpoints are the same.
Step 3:
Because they both yield the same y-value of 8, we know that all requirements are satisfied, which means we can now find all values of c within the open interval (-2,2) where f’(x) = 0.
Therefore, by using this process, we have found three values where the slope of the tangent line is zero within the interval!
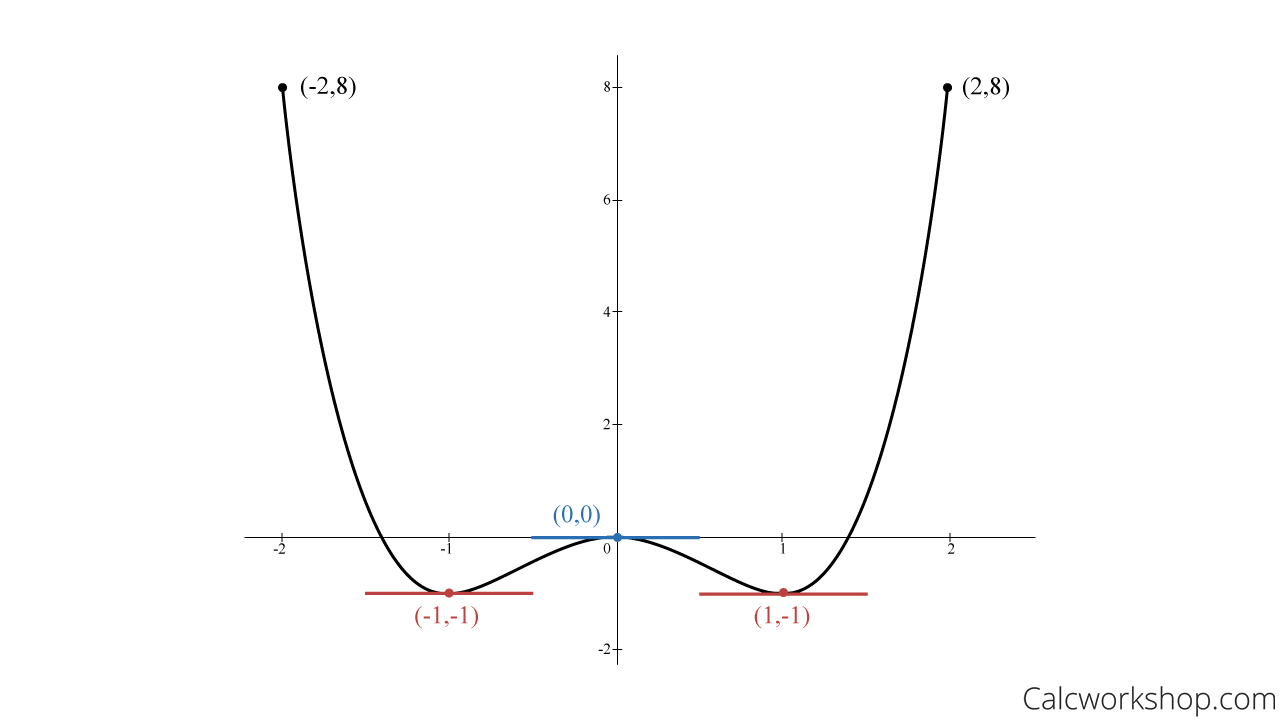
Rolles Theorem Closed Interval Max Min
See how easy that is!
Rolle’s Theorem Vs Extreme Value Theorem
It’s important to note the subtle but important difference between Rolle’s Theorem and the Extreme Value Theorem.
As a reminder, the Extreme Value Theorem states that a continuous function on a closed interval [a,b] must have both a minimum and maximum on the interval. These extrema values can, and often do, occur at the endpoints.
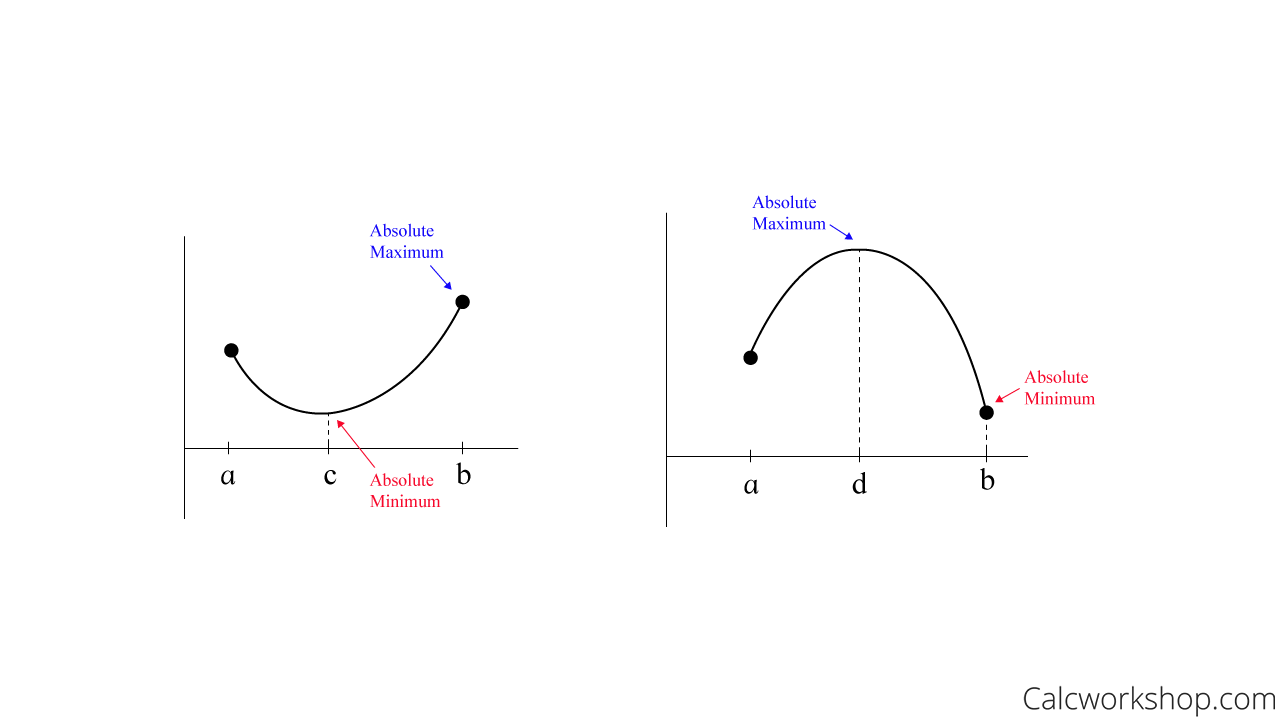
Absolute Maximum And Minimum
But what Rolle’s Theorem guarantees are the existence of an extreme value in the open interval, not including the endpoints.

Rolle’s Theorem – Critical Numbers
Together we will work through numerous examples, where we will first determine if Rolle’s Theorem applies and if so, we will find the point(s) where.
Let’s get after it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.