What if I told you that vector spaces and subspaces are like the continental United States and the great state of Colorado?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Analogy: Vector Spaces as the United States
Think of it like this.
The United States is huge!
With bustling cities and towns, dense forests, sprawling deserts, rolling hills, spacious skies, amber waves of grain, and purple mountain majesty … just borrowing a few words from the song America, the Beautiful.
Each region and state are unique, thus, making it difficult to show or “prove” its splendor.
So instead of trying to prove every aspect of what makes the United States exceptional, which would be quite an extensive list, we will choose just one state to focus on.
Because if we can show that this one state is amazing by association, we have thus proven that all 50 states are also amazing.
That’s the idea of vector spaces and subspaces. The continental United States is the vector space containing 48 connecting states (vectors).
Colorado is the subspace, a smaller vector space within the larger space. If we can show that Colorado has all the properties we need and want, then that means the continental United States does as well.
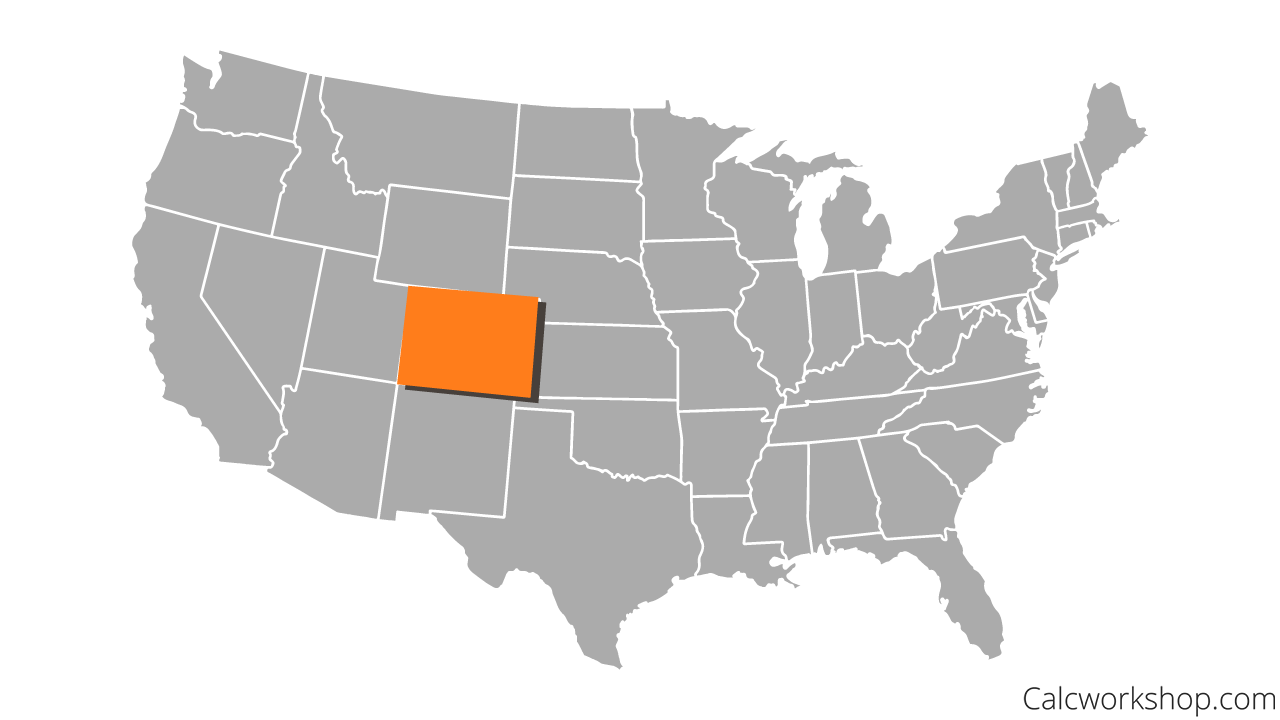
Vector Space Subspace (US Map)
Axioms of Vector Spaces
Okay, what qualities or properties do we need to prove?
You see, a vector space is a nonempty set \(V\) of vectors (objects) on which two operations, addition, and scalar multiplication, are defined and subject to ten rules or axioms.
The axioms hold for all vectors \(\vec{u}, \vec{v}\), and \(\vec{w}\) in \(\mathrm{V}\) and for all scalars \(\mathrm{c}\) and \(\mathrm{d}\) :
- The sum of \(\vec{u}\) and \(\vec{v}\), denoted \(\vec{u}+\vec{v}\), is in \(\mathrm{V}\).
- \(\vec{u}+\vec{v}=\vec{v}+\vec{u}\)
- \((\vec{u}+\vec{v})+\vec{w}=\vec{u}+(\vec{v}+\vec{w})\)
- There is a zero vector \(\overrightarrow{0}\) in \(\mathrm{V}\) such that \(\vec{u}+\overrightarrow{0}=\vec{u}\)
- For each \(\vec{u}\) in \(\mathrm{V}\), there is a vector \(-\vec{u}\) in \(\mathrm{V}\) such that \(\vec{u}+(-\vec{u})=\overrightarrow{0}\)
- The scalar multiple of \(\vec{u}\) by c, denoted \(\overrightarrow{c u}\), is in \(\mathrm{V}\).
- \(c(\vec{u}+\vec{v})=c \vec{u}+c \vec{v}\)
- \((c+d) \vec{u}=c \vec{u}+d \vec{u}\)
- \(c(d \vec{u})=(c d) \vec{u}\)
- \(1\vec{u}=\vec{u}\)
Proving Whether a Set is a Vector Space
And to prove whether \(\mathrm{V}\) is a vector space, we must demonstrate that all ten axioms hold, or we must find a counterexample showing that \(\mathrm{V}\) is not a vector space.
An Example of a Set Not Being a Vector Space
For example, assume we let \(V=\left\{\left[\begin{array}{l}x \\ y\end{array}\right]: x \geq 0, y \geq 0\right\}\). Is \(\mathrm{V}\) a vector space?
To show that \(\mathrm{V}\) is a vector space, we must show that addition and scalar multiplication is preserved via the ten axioms. But, if we put our thinking caps on, we quickly realize something is amiss.
Knowing that \(V=\left[\begin{array}{l}x \\ y\end{array}\right]=\langle x, y\rangle\) is any vector such that \(x \geq 0, y \geq 0\), this limits us to the first quadrant where \(\mathrm{x}\) and \(\mathrm{y}\) are both positive.

Graphing Vector Space (First Quadrant)
The addition of two vectors, where \(\mathrm{x}\) and \(\mathrm{y}\) are positive, will also result in a vector where both elements are positive. Therefore, \(\mathrm{V}\) is closed under addition.
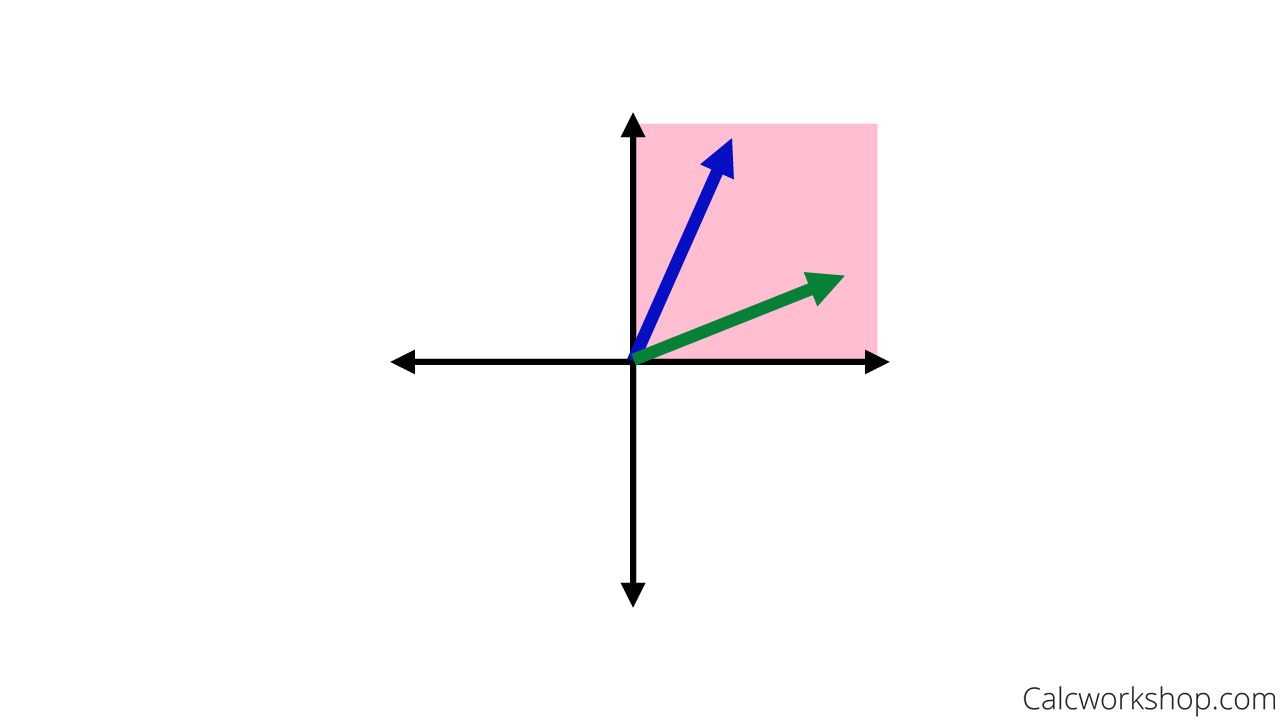
Vector Space (Closed Under Addition)
However, scalar multiplication is another thing entirely for \(\mathrm{V}\). Remember, \(\mathrm{c}\) is any real number, which means we can multiply our vector by a negative number.
What would that mean?
Suppose we let \(c=-2\).
Then, \(-2\left[\begin{array}{l}x \\ y\end{array}\right]=\langle-2 x,-2 y\rangle\) which when graphed on the xy-plane puts the vector in quadrant III, as shown below.
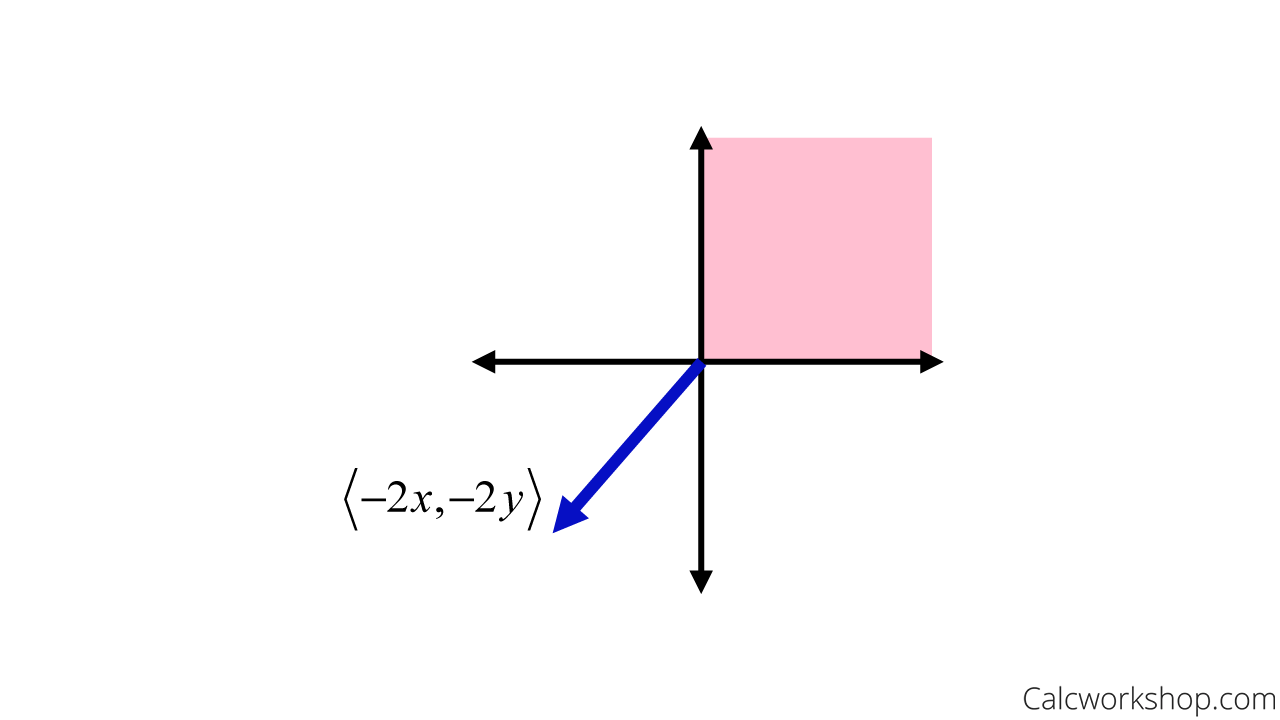
Scalar Multiplication (Not Vector Space)
But we’re only allowed to be in quadrant \(\mathrm{I}\), as \(x \geq 0, y \geq 0\). Consequently, \(\mathrm{V}\) is not closed under scalar multiplication, and we have just found a counterexample showing \(V\) is not a vector space.
Introduction to Subspaces
But gosh, what would happen if \(\mathrm{V}\) is a vector space?
We would have to prove all ten axioms!
And no one wants to do that!
So, instead of proving all ten, we will prove a subspace with only three axioms.
Again, think… if we can prove Colorado (subspace) is great, and if Colorado is inside the continental United States, then this proves that the United States (vector space) is also great.
A subspace of a vectors space \(\mathrm{V}\) is a subset \(\mathrm{H}\) of \(\mathrm{V}\) that has three properties:
- The zero vector of \(\mathrm{V}\) is in \(\mathrm{H}\), so it’s not empty.
- \(\mathrm{H}\) is closed under vector addition. That is, for each \(\vec{u}\) and \(\vec{v}\) in \(\mathrm{H}\), the sum \(\vec{u}+\vec{v}\) is also in \(\mathrm{H}\).
- \(\mathrm{H}\) is closed under multiplication by scalars. That is, for each \(\vec{u}\) in \(\mathrm{H}\) and each scalar \(\mathrm{c}\), the vector \(c \vec{u}\) is in \(\mathrm{H}\).
Now, we can all agree that proving three axioms is better than 10, but how do we begin?
The Idea of Span and Subspaces
Here’s the trick: a subspace is just like the span.
The \(\operatorname{Span}\left\{\vec{v}_{1}, \overrightarrow{v_{2}}, \ldots, \overrightarrow{v_{p}}\right\}\) is the set of all vectors that can be written as linear combinations \(\overrightarrow{v_{1}}, \overrightarrow{v_{2}}, \ldots, \overrightarrow{v_{p}}\), such that:
\begin{equation}
\operatorname{Span}\left\{\overrightarrow{v_1}, \overrightarrow{v_2}, \ldots, \overrightarrow{v_p}\right\}=c_1 \vec{v}_1+c_2 \vec{v}_2+\ldots+c_p \overrightarrow{v_p}
\end{equation}
Think of it like a subset.
If a subset of \(\mathbb{R}^{n}\) is any collection of points in \(\mathbb{R}^{n}\), then a subspace is a subset of the vector space.
Therefore, given any subspace \(\mathrm{H}\) of \(\mathrm{V}\), a spanning set (i.e., generating set) for H is a set \(\left\{\vec{v}_{1}, \overrightarrow{v_{2}}, \ldots, \overrightarrow{v_{p}}\right\}\) in \(\mathrm{H}\) such that:
\begin{equation}
H=\operatorname{Span}\left\{\vec{v}_1, \overrightarrow{v_2}, \ldots, \overrightarrow{v_p}\right\}
\end{equation}
Proving a Set is a Vector Space
Let’s look at an example.
Suppose \(\mathrm{W}\) is the set of all vectors of the form \((3 a+b, c-2 a, 5 b-c)\).
Where \(\mathrm{a}, \mathrm{b}\) and c represent arbitrary real numbers, and we want to show that \(\mathrm{W}\) is a vector space.
\begin{aligned}
W & =(3 a+b, c-2 a, 5 b-c) \\
& =\left[\begin{array}{c}
3 a+b \\
c-2 a \\
5 b-c
\end{array}\right]
\end{aligned}
First, let’s write the vectors in \(\mathrm{W}\) as column vectors.
\begin{aligned}
W & =\left[\begin{array}{c}
3 a+b \\
c-2 a \\
5 b-c
\end{array}\right] \\
& =\left[\begin{array}{c}
3 a+b \\
-2 a+c \\
5 b-c
\end{array}\right] \\
& =a\left[\begin{array}{c}
3 \\
-2 \\
0
\end{array}\right]+b \underbrace{\left[\begin{array}{c}
1 \\
0 \\
5
\end{array}\right]}_{v_{1}}+c \underbrace{c\left[\begin{array}{c}
0 \\
1 \\
-1
\end{array}\right]}_{v_{3}}
\end{aligned}
Now, let’s check to see if the zero vector can be found by letting \(a, b\), and \(c\) be zero.
\begin{aligned}
a\left[\begin{array}{c}
3 \\
-2 \\
0
\end{array}\right]+b\left[\begin{array}{l}
1 \\
0 \\
5
\end{array}\right]+c\left[\begin{array}{c}
0 \\
1 \\
-1
\end{array}\right] & \rightarrow 0\left[\begin{array}{c}
3 \\
-2 \\
0
\end{array}\right]+0\left[\begin{array}{l}
1 \\
0 \\
5
\end{array}\right]+0\left[\begin{array}{c}
0 \\
1 \\
-1
\end{array}\right] \\
& =\left[\begin{array}{l}
0 \\
0 \\
0
\end{array}\right]
\end{aligned}
Since zero vector is in the vector space, we can now see if the set of vectors spans W by looking for a consistent matrix using elementary row operations.
\begin{aligned}
\left[\begin{array}{ccc}
3 & 1 & 0 \\
-2 & 0 & 1 \\
0 & 5 & -1
\end{array}\right] & \sim\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]
\end{aligned}
Therefore, \(\mathrm{W}\) is a vector space as set \(\left\{\left[\begin{array}{c}3 \\ -2 \\ 0\end{array}\right],\left[\begin{array}{l}1 \\ 0 \\ 5\end{array}\right],\left[\begin{array}{c}0 \\ 1 \\ -1\end{array}\right]\right\}\) spans W.
See, it’s easy!
Next Steps
In this lesson, you will:
- Learn how to prove vector spaces
- Find counterexamples
- Find a set of vectors that span a vector space
- Determine how many vectors are in the span
- Check if W is in the subspace spanned by the vectors or by the columns of matrix A
Get ready to explore these concepts, and let’s get started!
Video Tutorial w/ Full Lesson & Detailed Examples

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.