To truly master linear algebra, you must fully grasp the power of vectors because vectors are the key to understanding matrices.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Why?
Because a vector is actually a matrix in disguise!
Defining Vectors and Vector Equations
So, what are vectors or vector equations?
A vector is a quantity with both magnitude (length) and direction. If I tell you to “walk 3 miles,” this only tells you the magnitude or length I wish you to walk. But if I say, “Walk 3 miles north by northwest,” then I’m giving you both a magnitude and direction- a vector!
Vector Notation and Operations
And two vectors are equivalent if they have the same size and direction and only differ in position (i.e., \(\mathbf{u}=\mathbf{v})\).

Equivalent Vectors (Same Length & Direction)
Vector Addition and Scalar Multiplication

Vector Scalar Multiplication

Vector – Negative Scalar Multiplication
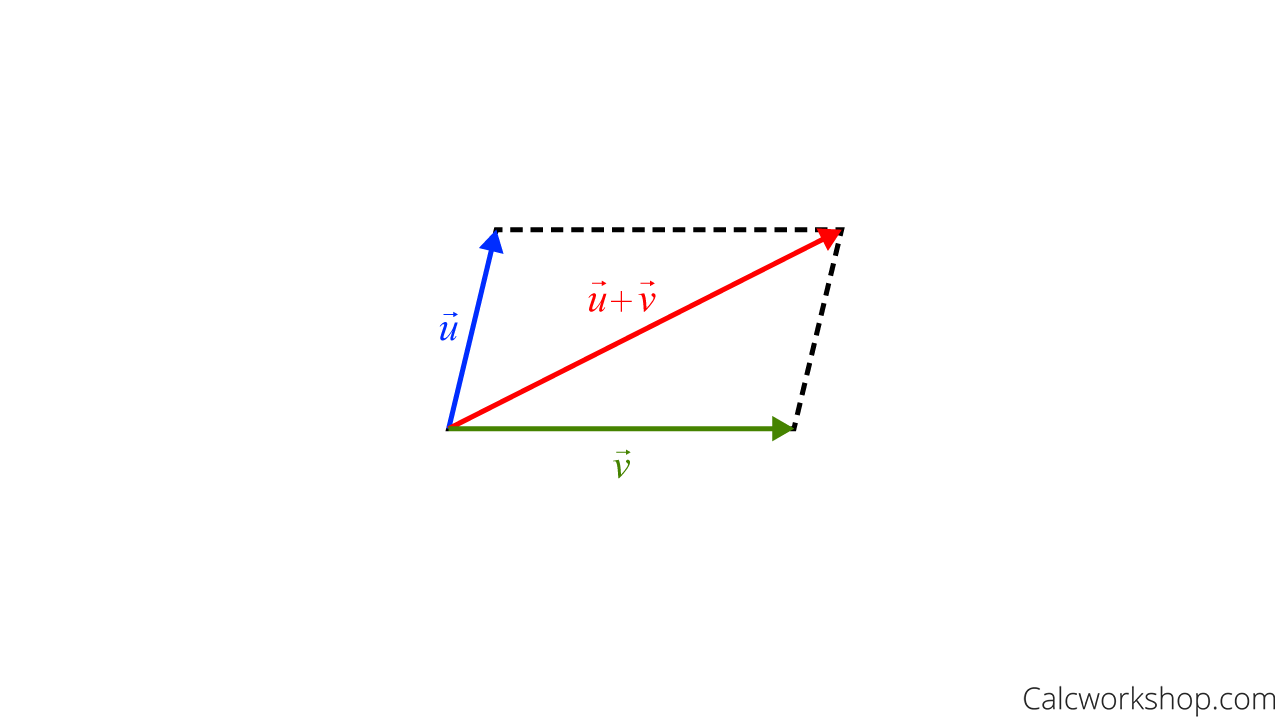
Vector Addition – Parallelogram Method
Okay, so all of this should make sense to us, or at least dust off the cobwebs from when we first learned about vectors from precalculus.
But now it’s time to talk about vector equations, as they are any function that takes on one or more variables and returns a vector.
The best way to make sense of this is, to begin with an ordered pair in \(\mathbb{R}^{2}\). Now, \(\mathbb{R}^{2}\) means the set of all vectors with two entries. But more simply, \(\mathbb{R}^{2}\) refers to the xy-plane or the Cartesian plane.
Vector Spaces and Column Vectors
But here’s what is so cool… any coordinate \((x, y)\) can be written as a vector, sometimes called a column vector, \(\left(\begin{array}{l}x \\ y\end{array}\right)\) in the plane \(\mathbb{R}^{2}\)!
For example, the following are two-entry vectors. Notice that each has an initial point at the origin and a terminal point at the ordered pair.
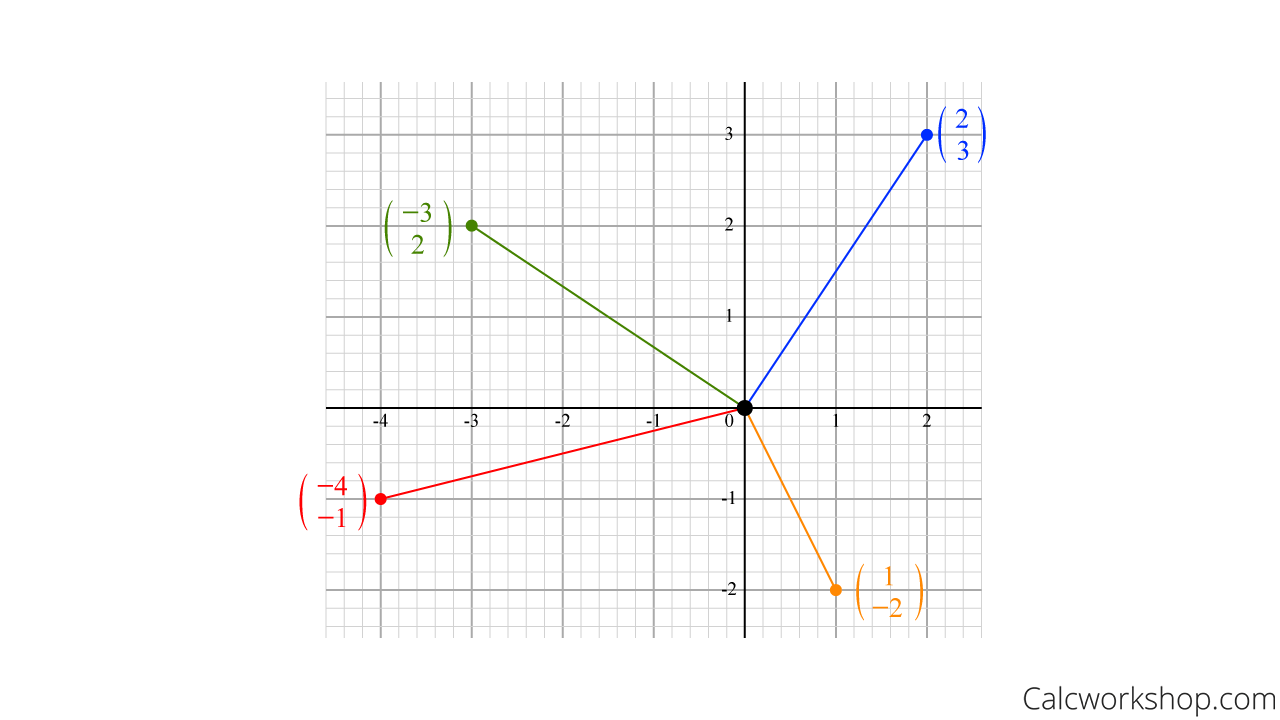
Graphing Vectors – Example
But there’s more to life than just two-entry vectors! Let’s look at \(\mathbb{R}^{3}\), which is the set of all ordered triples of real numbers and is also called 3-space (i.e., 3-D vector).
For example, the ordered triple in three-space has an initial point at the origin and terminal point \((2,4,5)\).
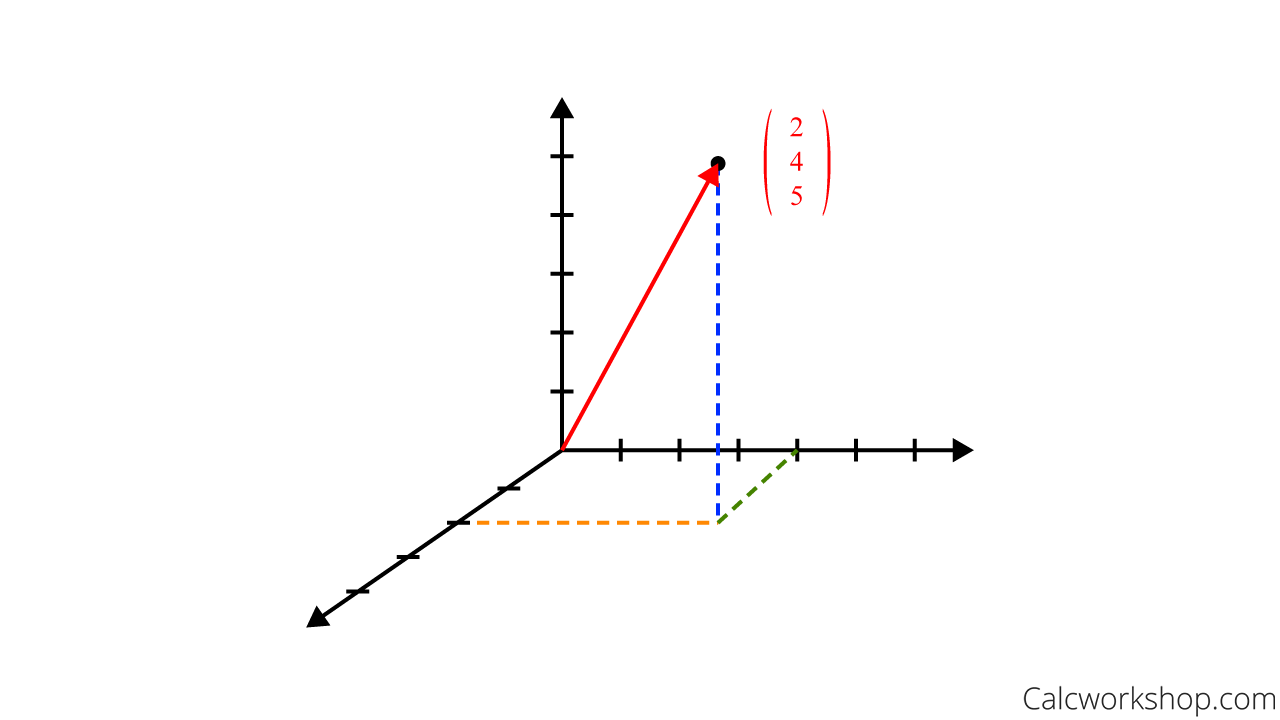
Plotting a Vector in Three Space
Extending Vectors to Multidimensional Space
While we can only graph vectors in \(\mathbb{R}^{2}\) (i.e., \(2 \times 1\) column matrices) and \(\mathbb{R}^{3}\) (i.e., \(3 \times 1\) column matrices) we can carry out calculations, analysis, and arithmetic for n-tuples of real numbers in multidimensional space that we denote as \(\mathbb{R}^{n}\), pronounced “r-n” for \(n \times 1\) column matrices.
Basic Properties of Vectors
Additionally, there are some basic properties of vectors that are important for all vectors \(\mathbf{u}, \mathbf{v}, \mathbf{w}\) in \(\mathbb{R}^{n}\) and all scalars c and \(\mathrm{d}\):
- \(\vec{u}+\vec{v}=\vec{v}+\vec{u}\)
- \((\vec{u}+\vec{v})+\vec{w}=\vec{u}+(\vec{v}+\vec{w})\)
- \(\vec{u}+\overrightarrow{0}=\overrightarrow{0}+\vec{u}=\vec{u}\)
- \(\vec{u}+(-\vec{u})=(-\vec{u})+\vec{u}=\overrightarrow{0}\)
- \(c(\vec{u}+\vec{v})=c \vec{u}+c \vec{v}\)
- \((c+d) \vec{u}=\vec{u}+d \vec{u}\)
- \(c(d \vec{u})=(c d) \vec{u}\)
- \(\overrightarrow{1 u}=\vec{u}\)
- \(\overrightarrow{0}=\left[\begin{array}{c}0 \\ 0 \\ \vdots \\ 0\end{array}\right]\), where \(\overrightarrow{0}\) is called the zero vector.
Linear Combination of Vectors
And this brings us to an incredibly important idea: a linear combination of vectors.
Given vectors \(v_{1}, v_{2}, \ldots, v_{n}\) in \(\mathbb{R}^{n}\) and scalars \(c_{1}, c_{2}, \ldots, c_{n}\), then \(c_{1} v_{1}+c_{2} v_{2}+\ldots+c_{n} v_{n}\) is called a linear combination of \(v_{1}, v_{2}, \ldots, v_{n}\) with weights \(c_{1}, c_{2}, \ldots, c_{n}\).
Okay, but why is this helpful?
Arithmetic with Column Matrices
Because it allows us to perform arithmetic with column matrices!
For example, suppose
\begin{aligned}
\bar{a} & =\left[\begin{array}{c}1 \\ -3\end{array}\right] \\
\bar{b} & =\left[\begin{array}{l}3 \\ 2\end{array}\right]
\end{aligned}
Find the following linear combinations:
\begin{aligned}
\bar{a}+\bar{b} & =\left[\begin{array}{c}
1 \\
-3
\end{array}\right]+\left[\begin{array}{l}
3 \\
2
\end{array}\right] \\
& =\left[\begin{array}{c}
1+3 \\
-3+2
\end{array}\right] \\
& =\left[\begin{array}{c}
4 \\
-1
\end{array}\right]
\end{aligned}
\begin{aligned}
5 \bar{a}+2 \bar{b} & =5\left[\begin{array}{c}1 \\ -3\end{array}\right]+2\left[\begin{array}{l}3 \\ 2\end{array}\right] \\
& =\left[\begin{array}{c}5 \\ -15\end{array}\right]+\left[\begin{array}{l}6 \\ 4\end{array}\right] \\
& =\left[\begin{array}{c}5+6 \\ -15+4\end{array}\right] \\
& =\left[\begin{array}{c}11 \\ -11\end{array}\right]
\end{aligned}
\begin{aligned}
\bar{b}-2 \bar{a} & =\left[\begin{array}{c}3 \\ 2\end{array}\right]-2\left[\begin{array}{c}1 \\ -3\end{array}\right] \\
& =\left[\begin{array}{l}3 \\ 2\end{array}\right]-\left[\begin{array}{c}2 \\ -6\end{array}\right] \\
& =\left[\begin{array}{c}3-2 \\ 2-(-6)\end{array}\right] \\
& =\left[\begin{array}{l}1 \\ 8\end{array}\right]
\end{aligned}
Isn’t it cool that we can linearly combine vectors just like we do with variables?
Linear Algebra Key Ideas: Spanning Sets
In fact, one of the key ideas in linear algebra is that the collection of all vectors that can be written in the form \(c_{1} v_{1}+c_{2} v_{2}+\ldots+c_{n} v_{n}\) is the subset of \(\mathbb{R}^{n}\) spanned (generated) by \(v_{1}, v_{2}, \ldots, v_{n}\), denoted as \(\operatorname{Span}\left\{v_{1}, v_{2}, \ldots, v_{n}\right\}\).
Think of it this way, imagine you want to travel the world. Well, you can “span” the globe using various means of travel: ship, plane, car, train, etc. This collection of options is similar to the spanning set, as they all find ways to formulate a solution or means for our desire to travel.
Next Steps
In this video, you’re going to grasp the concepts of vectors and vector equations, and unravel the relationship between vectors and matrices. Here’s what you can look forward to:
- Applying properties of vectors
- Performing basic vector operations
- Working through examples to identify if a vector is a Linear Combination of another vector
- Determining if a vector is within the Span
- Writing an equivalent system of equations for a given vector equation and vice versa
- Constructing a vector as a linear combination of a set of given vectors
- Answering foundational questions about Vector Equations, Linear Combinations, and the Spanning Set
It’s time to dive in and make vectors and vector equations your strength!
Video Tutorial w/ Full Lesson & Detailed Examples

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.