Vector Equation
How To Write & Find 'Em w/ Examples!

What is a vector equation?

And how do you use it to write an equation of a line in the xy-plane?

Point and slope!

And the same thing is true even in the three-dimensional space!

How?

Let’s find out.

Vector Equation Of A Line

The vector equation of a line \(L\) in three-space is determined when we know a point \(P_{0}\left(x_{0}, y_{0}, z_{0}\right)\) on \(L\) and the direction of \(L\).

\begin{equation}
\vec{r}=\vec{r}_{0}+t \vec{v}, t \in \mathbb{R}
\end{equation}

• \(\vec{r}=\overrightarrow{0 P}\) is the position vector from the origin to an arbitrary point P(x,y,z) on line \(L\).
• \(\vec{r}_{0}=\overrightarrow{0 P}_{0}\) is the position vector from the origin to a specific point \(P_{0}\left(x_{0}, y_{0}, z_{0}\right)\) on line \(L\).
• \(\vec{v}=\overrightarrow{P_{0} P}\) is a vector parallel to the line called the direction vector of the line.
• \(t\) is a real number corresponding to the arbitrary point \(P\).

But here’s what is important…

…the direction vector is our slope! And since we know that parallel lines have the same slope, knowing that \(\vec{u}\) and \(\vec{v}\) are parallel vectors, we can write our equation.

\begin{equation}
L: \vec{r}=\langle\text { point }\rangle+t\langle\text { slope vector }\rangle
\end{equation}

See!

Writing an equation of a line in 3D is just like writing an equation of a line in 2D. All we need is a point and slope.

Example

Let’s look at an example.

Find a vector equation of the line \(L\) that passes through the points A(3,2,1) and B(0,-1,2).

First, we will pick one of the two points given. For ease of purpose let’s choose point A. Next, we will find our direction vector, which is our slope.

\begin{equation}
\vec{v}=\overrightarrow{A B}=\langle 0-3,-1-2,2-1\rangle=\langle-3,-3,1\rangle
\end{equation}

Lastly, we write our equation knowing \(\vec{r}=\vec{r}_{0}+t \vec{v}\).

\begin{equation}
\begin{aligned}
&L: \vec{r}=\langle\text { point }\rangle+t\langle\text { slope vector }\rangle \\
&L: \vec{r}=\langle 3,2,1\rangle+t\langle-3,-3,1\rangle, t \in \mathbb{R}
\end{aligned}
\end{equation}

Easy, right?

Parametric Equation Of A Line

But just like we learned in Algebra, where there are various forms for an equation of a line such as slope-intercept form, point-slope form, and standard form, there are various ways we can write our equation of a line in a plane.

Namely, parametric form and symmetric form.

Given the vector representation of an equation of a line in three-space, we can rewrite the vector as a collection of parametric equations of a line in \(\mathbb{R}^{3}\) as follows:

\begin{equation}
\begin{array}{c|c}
\text { Vector Form } & \text { Parametric Form } \\
\hline \vec{r}=\vec{r}_{0}+t \vec{v}, t \in \mathbb{R} & \vec{r}=\left\langle x_{0}+a t, y_{0}+b t, z_{0}+c t\right\rangle, t \in \mathbb{R} \\
\vec{r}=\left\langle x_{0}, y_{0}, z_{0}\right\rangle+t\langle a, b, c\rangle, t \in \mathbb{R} & \langle x, y, z\rangle=\left\langle x_{0}+a t, y_{0}+b t, z_{0}+c t\right\rangle, t \in \mathbb{R} \\
\vec{r}=\left\langle x_{0}+a t, y_{0}+b t, z_{0}+c t\right\rangle, t \in \mathbb{R} & \begin{array}{l}
x=x_{0}+a t \\
y=y_{0}+b t \\
z=z_{0}+c t
\end{array}
\end{array}
\end{equation}

Example

So, using our example above, let’s find the parametric equations of line \(L\) that passes through the points A(3,2,1) and B(0,-1,2).

As we found our vector equation to be L:\(\vec{r}=\langle 3,2,1\rangle+t\langle-3,-3,1\rangle\), where \(t\) \(\in \mathbb{R}\), all we have to do now is simply rewrite our parametric equations by grouping the x, y, and z components together.

\begin{equation}
\begin{aligned}
&\vec{r}=\langle 3,2,1\rangle+t\langle-3,-3,1\rangle \\
&\vec{r}=\langle 3-3 t, 2-3 t, 1+t\rangle \\
&\langle x, y, z\rangle=\langle 3-3 t, 2-3 t, 1+t\rangle \\
&x=3-3 t, \quad y=2-3 t, \quad z=1+t
\end{aligned}
\end{equation}

Simple!

Symmetric Equation Of A Line

Alright, now let’s look at writing our equation in symmetric form.

This is easily done by transforming our parametric equations so that we solve for the parameter t.

If

\begin{equation}
\begin{aligned}
&x=x_{0}+a t \quad \Rightarrow \quad t=\frac{x-x_{0}}{a} \\
&y=y_{0}+b t \quad \Rightarrow \quad t=\frac{y-y_{0}}{b} \\
&z=z_{0}+c t \quad \Rightarrow \quad t=\frac{z-z_{0}}{c}
\end{aligned}
\end{equation}

And since all three of our parametric equations are equal to t, and as long as \(\langle a, b, c\rangle \neq\langle 0,0,0\rangle\) we can simplify our equation into its symmetric form.

\begin{equation}
\frac{x-x_{0}}{a}=\frac{y-y_{0}}{b}=\frac{z-z_{0}}{c}
\end{equation}

Example

So, once again, let’s take our previous example where \(L\) it a line that passes through the points \(A(3,2,1)\) and \(B(0,-1,2)\) and rewrite it in symmetric form.

We have already determined both the vector and parametric form as follows:

Lastly, we write our equation knowing \(\vec{r}=\vec{r}_{0}+t \vec{v}\).

\begin{equation}
L: \vec{r}=\langle 3,2,1\rangle+t\langle-3,-3,1\rangle \text { and } x=3-3 t, \quad y=2-3 t, \quad z=1+t
\end{equation}

Now, let’s take our parametric representation and solve each equation for \(t\) and set them equal to each other.

\begin{equation}
\begin{aligned}
&x=3-3 t \quad \Rightarrow \quad t=\frac{x-3}{-3} \\
&y=2-3 t \quad \Rightarrow \quad t=\frac{y-2}{-3} \\
&z=1+t \quad \Rightarrow \quad t=\frac{z-1}{1}
\end{aligned}
\end{equation}

So, our symmetric style is simply:

\begin{equation}
\frac{x-3}{-3}=\frac{y-2}{-3}=\frac{z-1}{1}
\end{equation}

Equation Of A Plane

Alright, so now that we know how to write equations of lines in 3 space let’s turn our attention to writing equations of planes.

Just like equations of lines, we only need a point and a slope to write an equation of a plane.

But the slope for the equation of a plane must a special type of vector — the normal vector!

The normal vector is the orthogonal (perpendicular) vector \(\vec{n}\) to the plane and is found using the cross product.

To obtain a scalar equation of a plane we write \(\vec{n}=\langle a, b, c\rangle, \vec{r}=\langle x, y, z\rangle, \text { and } \vec{r}_{0}=\left\langle x_{0}, y_{0}, z_{0}\right\rangle\) such that:

\begin{equation}
a\left(x-x_{0}\right)+b\left(y-y_{0}\right)+c\left(z-z_{0}\right)=0
\end{equation}

And by simplifying and collecting like terms, the scalar equation of the plane through \(P_{0}\left(x_{0}, y_{0}, z_{0}\right)\) with normal vector \(\vec{n}=\langle a, b, c\rangle\) can be expressed as \(a x+b y+c z+d=0\).

Example

For example, find an equation of the plane that passes through the points A(1,2,-3), B(-2,4,-1), and C(0,6,2).

First, we need to remember that we need two things to write an equation of a plane:

1. A Point On The Plane
2. The Normal Vector

Step 1:

So, let’s choose point A (it doesn’t matter which one we choose).

Step 2:

Now, let’s identify two vectors that lie in the plane so we can eventually use the cross product to find the normal vector.

\begin{equation}
\begin{aligned}
&\overrightarrow{A B}=\langle-2-1,4-2,-1-(-3)\rangle=\langle-3,2,2\rangle \\
&\overrightarrow{A C}=\langle 0-1,6-2,2-(-3)\rangle=\langle-1,4,5\rangle
\end{aligned}
\end{equation}

Next, it’s time to perform the cross-product to find the normal vector.

\begin{equation}
\vec{n}=\overrightarrow{A B} \times \overrightarrow{A C}=\left|\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
-3 & 2 & 2 \\
-1 & 4 & 5
\end{array}\right|=2 \vec{i}+13 \vec{j}-10 \vec{k}=\langle 2,13,-10\rangle
\end{equation}

Step 3:

Finally, to write the equation of the plane we just have to drop in our point A(1,2,-3) and normal slope, \(\vec{n}=\langle a, b, c\rangle=\langle 2,-13,-10\rangle\) into our equation and simplify.

\begin{equation}
\begin{aligned}
&a\left(x-x_{0}\right)+b\left(y-y_{0}\right)+c\left(z-z_{0}\right)=0 \\
&2(x-1)+13(y-2)-10(z-(-3))=0 \\
&2(x-1)+13(y-2)-10(z+3)=0 \\
&2 x+13 y-10 z-58=0
\end{aligned}
\end{equation}

And that’s it!

So, together we will learn how to write equations of lines and planes in three-dimensional coordinates, and discover how to write equations in write them in vector, parametric or symmetric forms.

Additionally, we will determine if two lines are parallel, perpendicular, intersecting or skew, and how to calculate the distance from a point to a plane.

It’s going to be exciting, so let’s jump right in.

Video Tutorial w/ Full Lesson & Detailed Examples (Video)

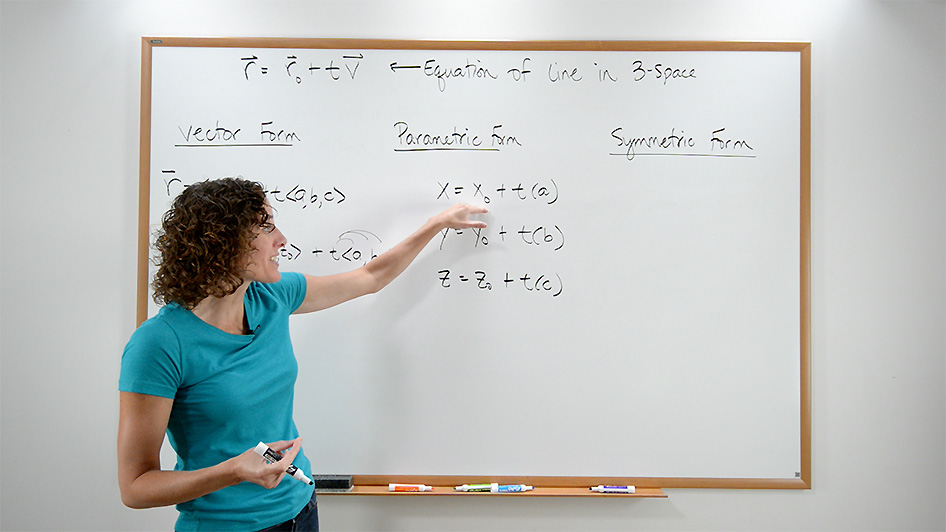
Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.