Did you know all we have to do to understand a three-dimensional object is to first look at its cross section?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Why?
Because a quadric surface is nothing more than a three-dimensional extension of a conic section.
This means that if we can identify the two-dimensional curve — line, ellipse, parabola, or hyperbola — then identifying and sketching the resulting surface in the three-dimensional space will be a snap.
Cross Section
But what do we mean by cross-section?
A cross section of an object or surface is what would be exposed or revealed if we slice the object with a plane:
The 2D sketch (i.e., cross-section) of the surface is called the trace.
For example, suppose we slice a cone with the xy-plane as seen in the image below. The resulting cross section is an ellipse, and the subsequent sketch of the slice in the 2D plane is the trace.
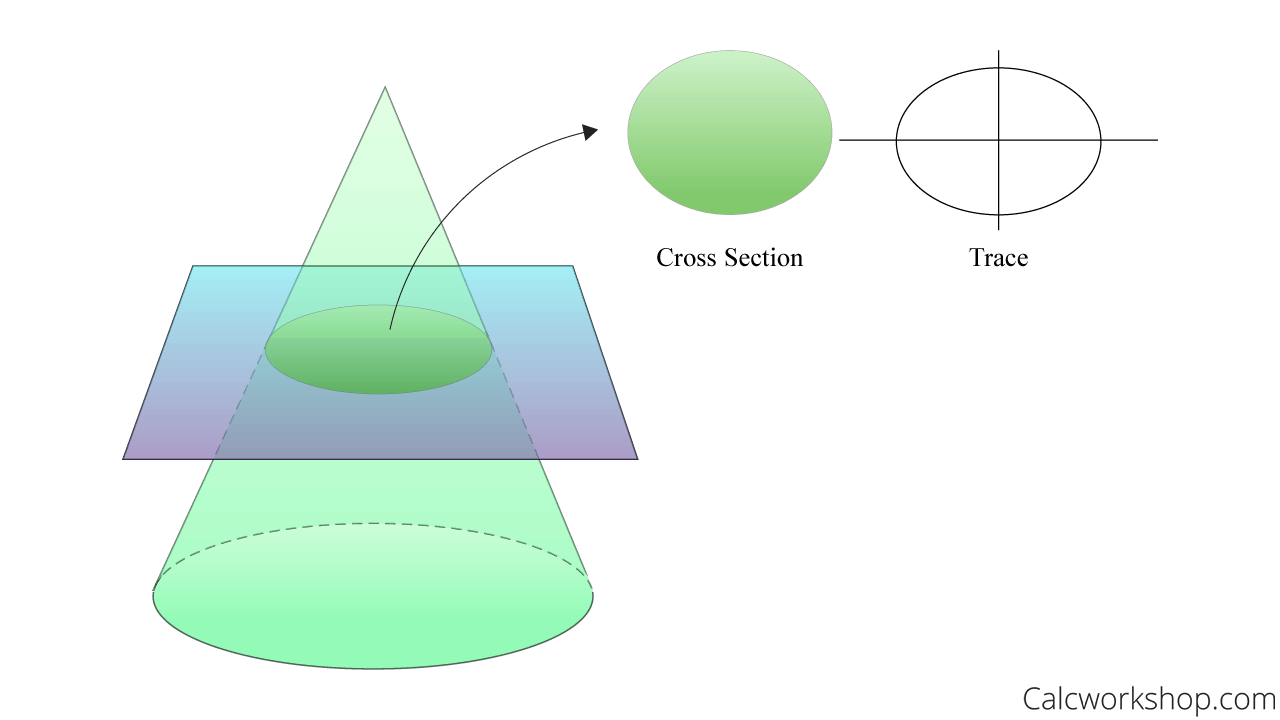
Cross Section Of A Cone
So, if the traces of a surface are nothing more than a cross-section created when the surface intersects a plane parallel to one of the coordinate planes, what’s a quadric surface?
Identifying Quadric Surfaces
Quadric surfaces are the graphs of equations that can be expressed in the form:
Please note that when a quadric surface intersects the coordinate plane (xy-plane, xz-plane, or yz-plane), the trace is a conic section:
- Line
- Parabola
- Circle
- Ellipse
- Hyperbola
Types of Quadric Surfaces
Let’s take a look by comparing the 2D curve with its 3D counterpart.
Circle Vs Cylinder
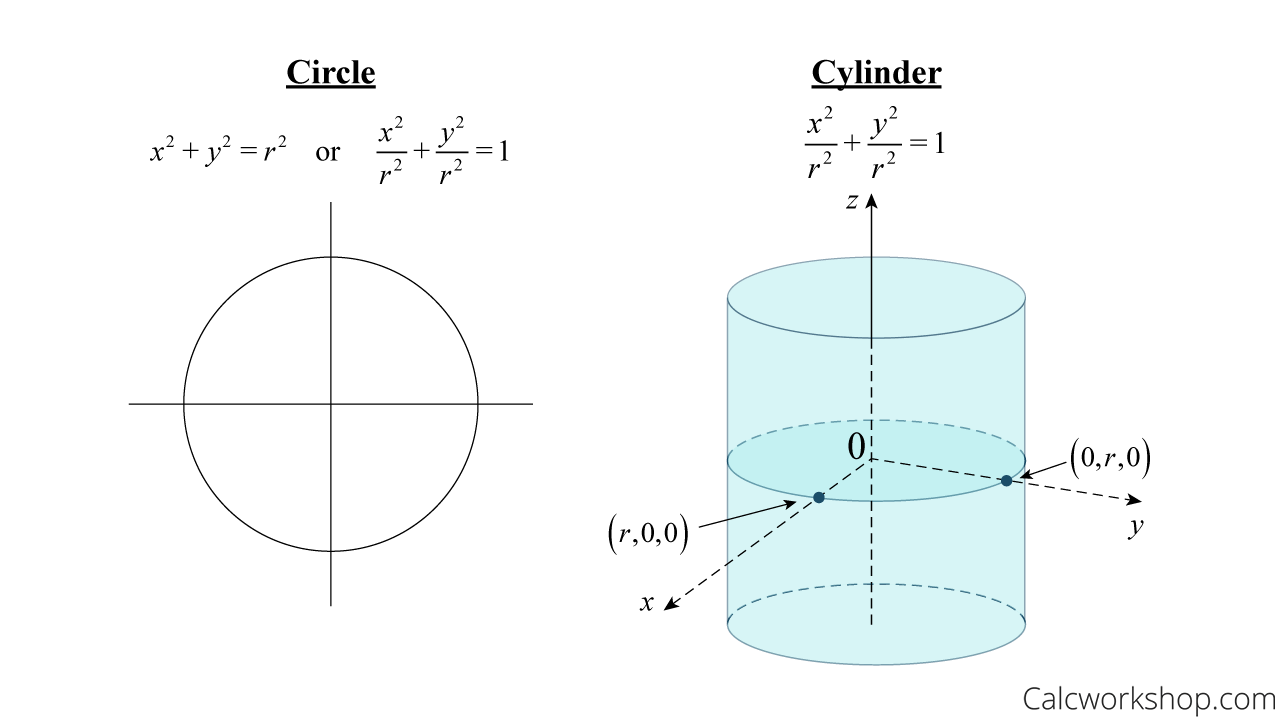
Circle vs. Cylinder (Equation & Graph)
The absence of the z-variable allows the three-dimensional solid to vary along the z-axis; thus, giving it height, and transforming it from a circle to a cylinder.
Ellipse vs Ellipsoid
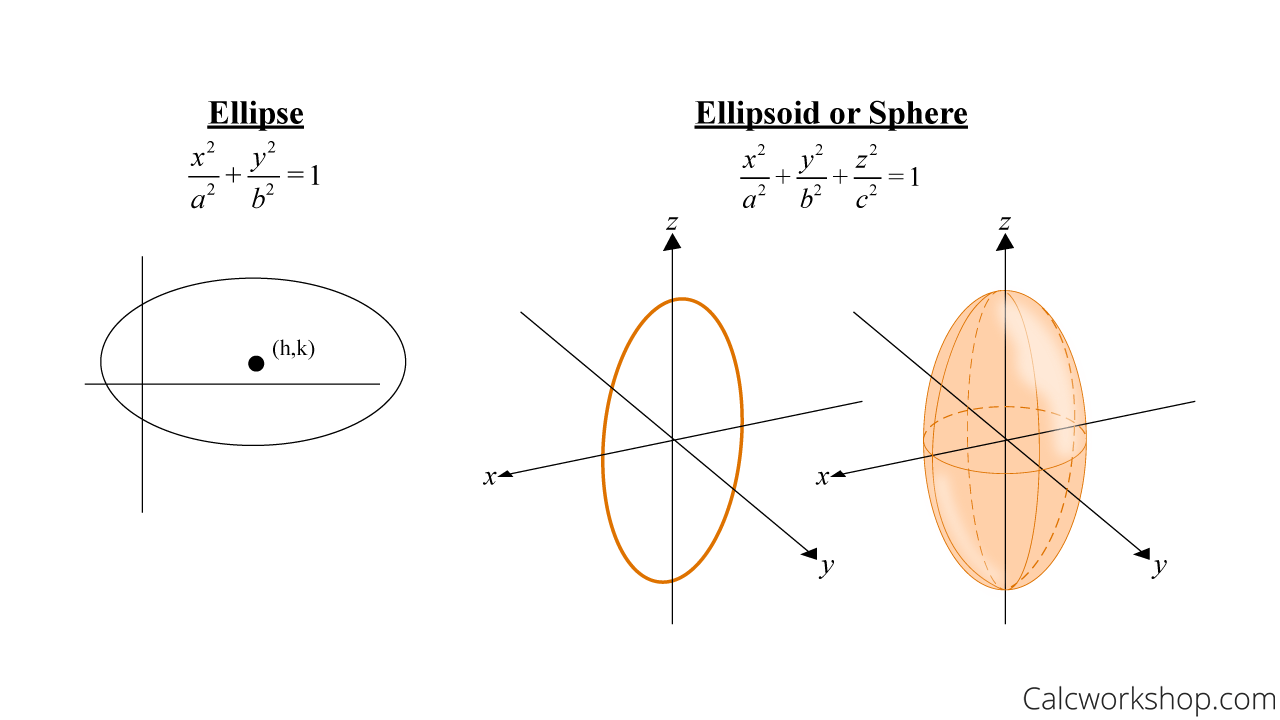
Ellipse vs. Ellipsoid or Sphere (Equation & Graph)
Each slice (trace) of the ellipsoid is an ellipse and all the signs are positive. Moreover, it’s important to note that if
Ellipse vs Cone
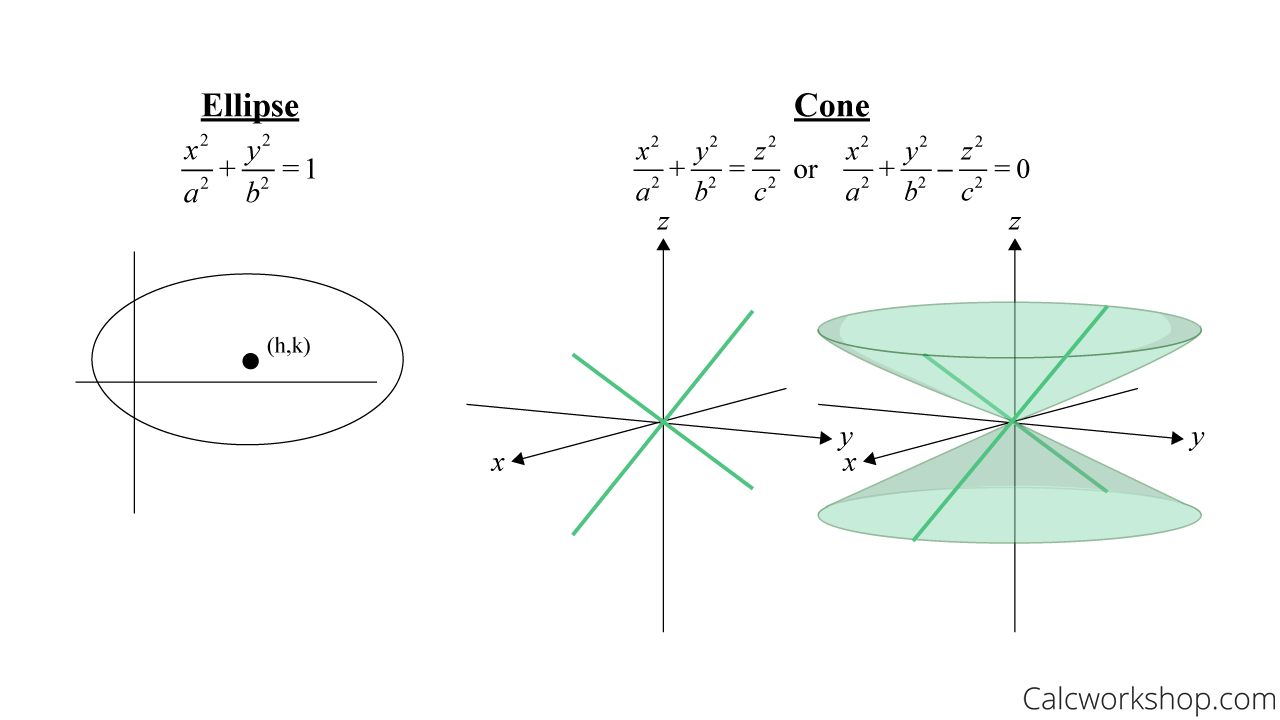
Ellipse vs. Cone (Equation & Graph)
Notice how two of the variables are on one side of the equation and the third is on the other. If we move all three variables to the same side the resulting equation is now equal to zero, not one, which tells us the resulting shape will be a cone.
Parabola vs Paraboloid
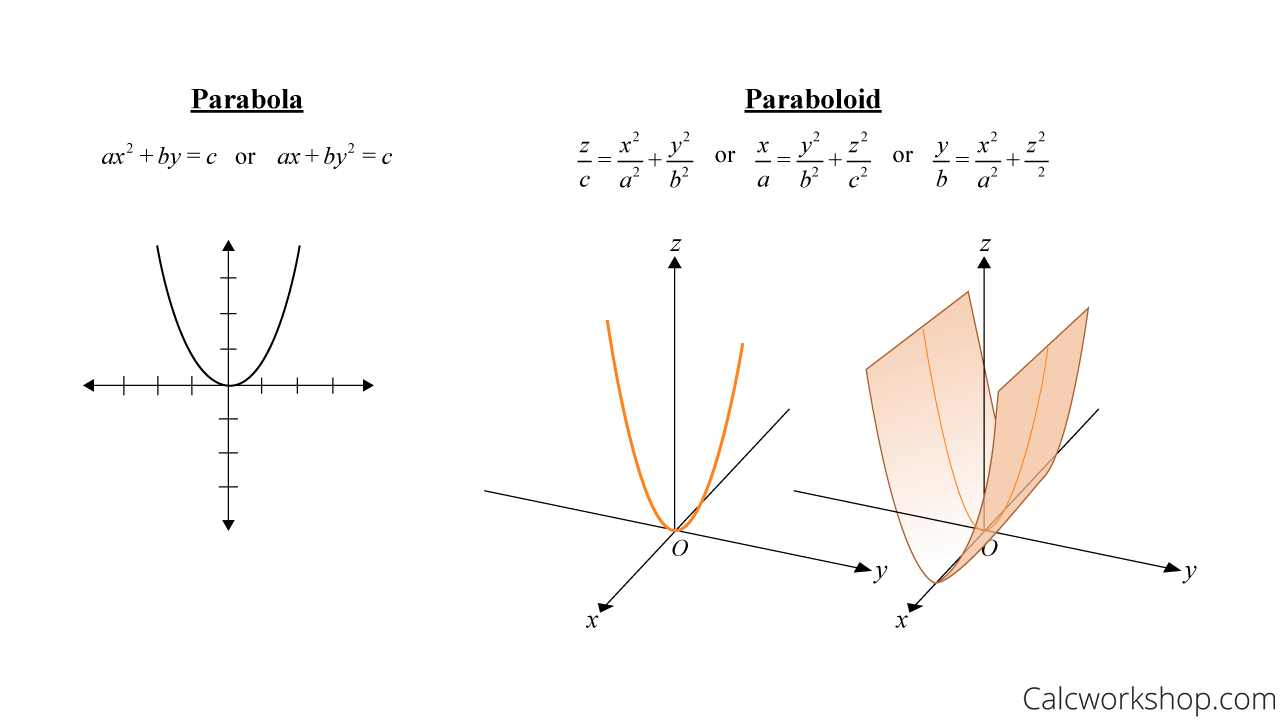
Parabola vs. Paraboloid (Equation & Graph)
Notice how one of the variables is not squared. This tells use it is a paraboloid and that it will open along the non-squared axis.
Hyperbola vs Hyperboloid of One-Sheet

Hyperbola vs. Hyperboloid Of One Sheet (Equation & Graph)
Notice how only “one” of the variables is negative. This tells use it is a hyperboloid of one-sheet. Additionally, the variable that is negative also indicates to which axis the hyperboloid will open.
Hyperbola vs Hyperboloid of Two-Sheet
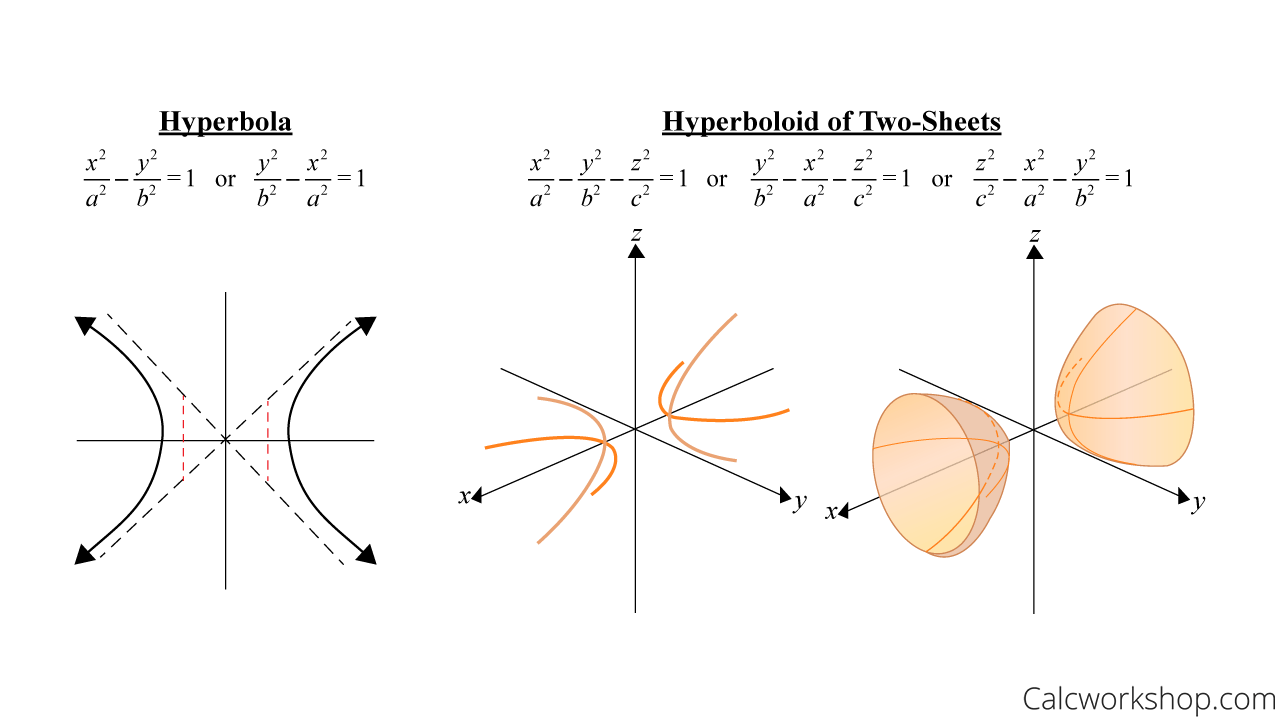
Hyperbola vs. Hyperboloid Of Two Sheets (Equation & Graph)
Notice how “two” of the variables are negative. This tells use it is a hyperboloid of two-sheets. And this time, the variable that is positive will indicate which axis the hyperboloid will open.
Elliptic Paraboloid & Hyperbolic Paraboloid
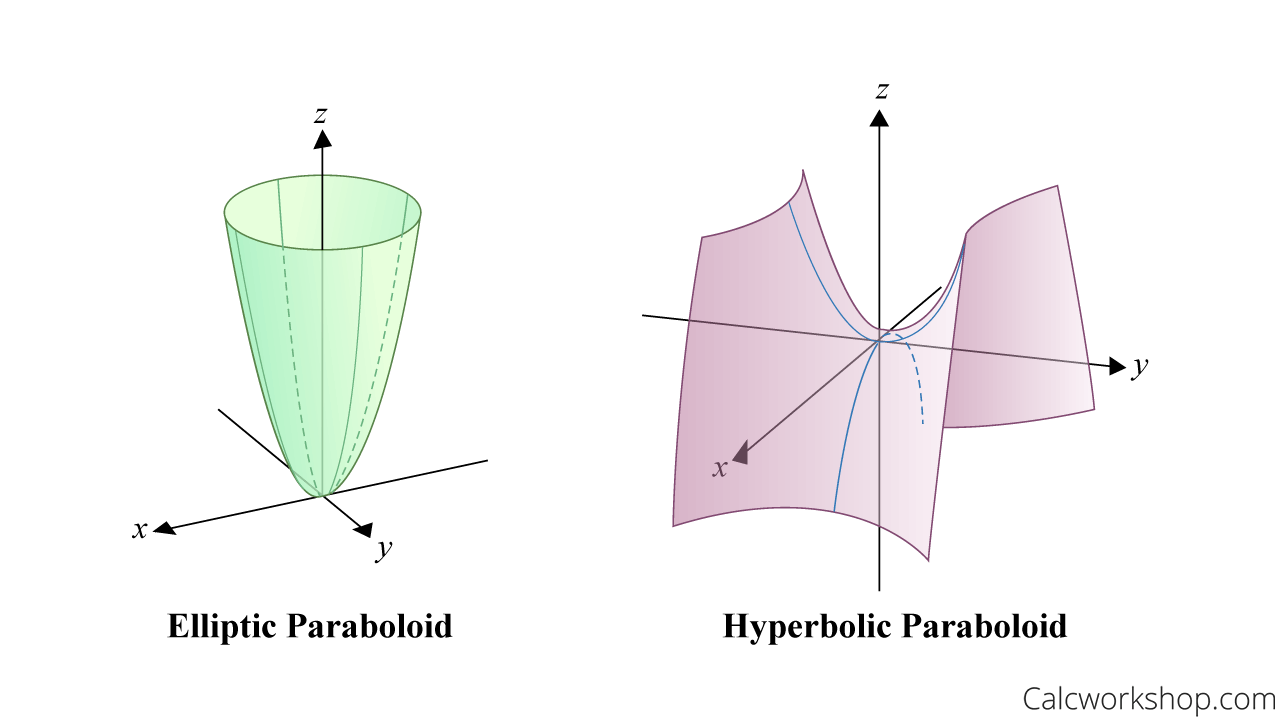
Hyperbolic And Elliptic Paraboloid 3D Graph
And here’s the cool part! We can even combine our quadric surfaces to yield such surfaces as elliptic paraboloids or hyperbolic paraboloids.
Traces Of Quadric Surfaces
So, how do we determine the resulting surface?
We look for traces.
Example
For instance, let’s name the shapes by identifying the traces:
First, we notice that one of the variables is not squared. This instantly tells us that we are dealing with a paraboloid. Now, all we have to do is determine what kind of paraboloid (i.e., elliptic, or hyperbolic)
How?
Finding traces means we let each variable become a constant (number), and identify it’s resulting curve.
- If
where is any constant, then which is a hyperbola. - If
where is any constant, then which is a parabola. - If
where is any constant, then which is a parabola. This means that
in the Cartesian coordinate system is a hyperbolic paraboloid that will open along the x-axis because it is the non-squared term.
Example
Let’s tackle this problem.
Name the shapes by identifying the traces
First, we notice that all of the variables are squared, but one of the variables is negative. This instantly tells us that we are dealing with a hyperboloid of one-sheet.
Let’s confirm our suspicions by finding the traces.
- If
where is any constant, then which is a hyperbola. - If
where is any constant, then which is a circle. - If
where is any constant, then which is a hyperbola. This confirms that our equation represents a circular hyperboloid of one sheet that will open along the y-axis because it is the negative term.
Easy, right?
Together in our video we will review our two-dimensional conic sections so we can quickly and easily identify the three-dimensional quadric surfaces.
We will learn how to find traces and sketch level curves, which are just a collection of traces or cross-sections of a graph, so we can easily identify and graph surfaces in 3-space.
Let’s jump on in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.