3D Dot Product (How-To w/ Step-by-Step Examples!)

How do you find the 3D dot product of two vectors?

Jenn (B.S., M.Ed.) of Calcworkshop® teaching dot product in 3d

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

Good question, and that’s exactly what you’re going to learn in today’s Calculus 3 class.

So did you know that we get a scalar when we multiply two vectors together?

It’s true.

The dot product, appropriately named for the raised dot signifying multiplication of two vectors, is a real number, not a vector.

And that is why the dot product is sometimes referred to as a scalar product or inner product.

So, the 3d dot product of $\vec{p} = ⟨ a, b, c ⟩$ and $\vec{q} = ⟨ d, e, f ⟩$ is denoted by $\vec{p} \cdot \vec{q}$ (read $\vec{p}$ dot $\vec{q}$ ) and given by $\vec{p} \cdot \vec{q} = a d + b e + c f$ .

So, all we have to do is multiply the corresponding elements and add the products!

Example – 3D Dot Product Of Two Vectors

Let’s make sure you got this by finding the dot product for each problem below.

Problem #1 – 2D Vectors
$⟨ 3, 2 ⟩ \cdot ⟨ - 1, 4 ⟩ = (3) (- 1) + (2) (4) = - 3 + 8 = 5$

Problem #2 – 3D Vectors
$⟨ - 5, - 3, 4 ⟩ \cdot ⟨ 6, - 2, 1 ⟩ = (- 5) (6) + (- 3) (- 2) + (4) (1) = - 30 + 6 + 4 = - 20$

Simple!

Dot Product Properties

And because the dot product behaves similarly to our property of multiplication, the following properties are easily shown for all vectors $\vec{p}$ , $\vec{q}$ , and $\vec{r}$ and scalar k.

$\begin{array}{ll} \vec{p} \cdot \vec{q} = \vec{q} \cdot \vec{p} & \vec{p} \cdot (\vec{q} + \vec{r}) = \vec{p} \cdot \vec{q} + \vec{p} \cdot \vec{r} \\ (\vec{p} + \vec{q}) \cdot \vec{r} = \vec{p} \cdot \vec{r} + \vec{q} \cdot \vec{r} & (k \vec{p}) \cdot \vec{q} = k (\vec{p} \cdot \vec{q}) = \vec{p} \cdot (k \vec{q}) \\ \vec{0} \cdot \vec{p} = 0 & \vec{p} \cdot \vec{p} = ‖ \vec{p} ‖^{2} \end{array}$

But, what’s so special about the dot product?

Well, the dot product doesn’t yield just any old number but a very special number indeed.

Dot products are used to determine the angle between two vectors and play a significant role in solving various physical problems such as force, navigation, and space curves.

Geometric Interpretation of the Dot Product

The angle $θ$ between $\vec{p}$ and $\vec{q}$ is defined to be the angle having the two vectors as its sides for which $0^{\circ} \leq θ \leq 180^{\circ}$ , then $\vec{p} \cdot \vec{q} = ‖ \vec{p} ‖ ‖ \vec{q} ‖$ $\cos θ$ or $\cos θ =$ $\frac{\vec{p} \cdot \vec{q}}{‖ \vec{p} ‖ ‖ \vec{q} ‖}$

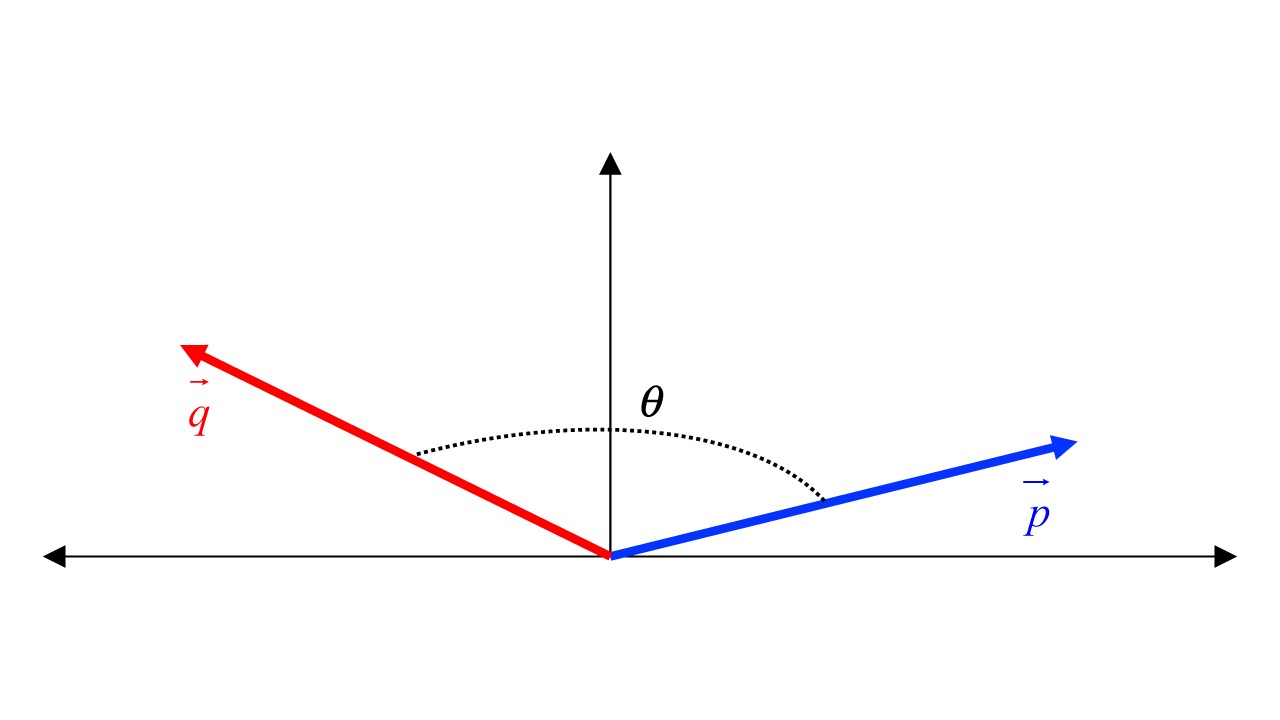
Dot Product Visualization

Example – Angle Between Two Vectors

For example, let’s find the angle between the following two vectors $\vec{a} = ⟨ 4, 3 ⟩ and \vec{b} = ⟨ 1, 2 ⟩$ .

Step 1:

First, we will calculate the dot product for our two vectors:

$\vec{p} \cdot \vec{q} = ⟨ 4, 3 ⟩ \cdot ⟨ 1, 2 ⟩ = 4 (1) + 3 (2) = 10$

Step 2:

Next, we will compute the magnitude for each of our vectors separately.

$\begin{aligned} ‖ \vec{a} ‖ = \sqrt{4^{2} + 3^{2}} = \sqrt{16 + 9} = \sqrt{25} = 5 \\ ‖ \vec{b} ‖ = \sqrt{1^{2} + 2^{2}} = \sqrt{1 + 4} = \sqrt{5} \end{aligned}$

Step 3:

Lastly, we will substitute our values into our formula to find our angle $θ$ .

$\begin{aligned} \vec{p} \cdot \vec{q} = ‖ \vec{p} ‖ ‖ \vec{q} ‖ ‖ \cos θ \\ 10 = (5) (\sqrt{5}) \cos θ \\ \cos θ = \frac{10}{(5) (\sqrt{5})} \\ \cos θ = 0.894 \\ θ = \cos^{- 1} (0.894) \\ θ = {26.57}^{\circ} \end{aligned}$

Not too bad!

And here’s something exciting. Depending on the value of the dot product, we can quickly determine if the angle between the vectors is acute, obtuse, or right.

$\begin{array}{cc} If the Dot Product is.. & Then the Angle between the vectors is.. \\ Positive & Acute \\ Negative & Obtuse \\ Zero & Right \end{array}$

Direction Cosines

But how can we use this knowledge to determine a vector?

As we know, a vector in two dimensions is determined by its direction and magnitude. But vectors in three dimensions are determined by their magnitude and three direction angles.

What?

Yes. Three direction angles, known as the directional cosines, help us to represent the angle located in the plane between a vector and each of the coordinate axes.

For $\vec{v} = ⟨ a, b, c ⟩$ the three direction angles are determined as follows:

$\cos α = \frac{a}{‖ \vec{v} ‖} \cos β = \frac{b}{‖ \vec{v} ‖} \cos γ = \frac{c}{‖ \vec{v} ‖}$

Where $\cos^{2} α + \cos^{2} β + \cos^{2} γ = 1$ , similar to the Pythagorean Identity.

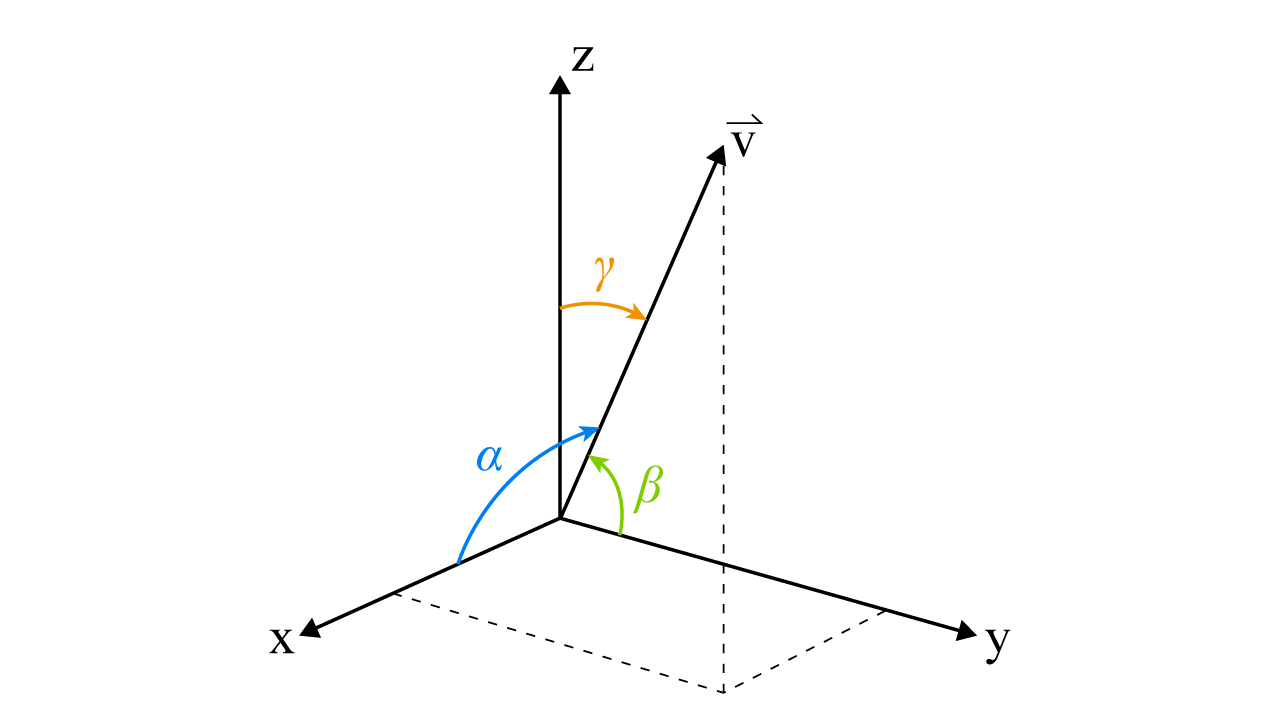
Direction Cosines

This means that $α$ is the direction angle between $\vec{v}$ and the positive x-axis, $β$ is the direction angle between $\vec{v}$ and the positive y-axis, and $γ$ is the direction angle between $\vec{v}$ and the positive z-axis.

Example – Direction Cosine Angles

Suppose we are given $\vec{v} = ⟨ 6, 2, - 3 ⟩$ . Let’s find the direction angles.

First, we need to find the magnitude of our vector.

$‖ \vec{v} ‖ = \sqrt{6^{2} + 2^{2} + (- 3)^{2}} = \sqrt{49} = 7$

Next, we will substitute our vector elements into our formulas and solve

If $\vec{v} = ⟨ \begin{array}{ccc} 6, 2, - 3 \\ a, b, c \end{array} ⟩$ and $‖ \vec{v} ‖ = 7, and \cos α = \frac{α}{‖ \vec{v} ‖}, \cos β = \frac{b}{‖ \vec{v} ‖}, and \cos γ = \frac{c}{‖ \vec{v} ‖}$ , then

$\begin{aligned} \cos α = \frac{6}{7} \cos β = \frac{2}{7} \cos γ = \frac{- 3}{7} \\ α = \cos^{- 1} (\frac{6}{7}) β = \cos^{- 1} (\frac{2}{7}) γ = \cos^{- 1} (\frac{- 3}{7}) \\ α = 31^{\circ} β = {73.4}^{\circ} γ = {115.4}^{\circ} \end{aligned}$

Nothing to it!

And understanding the dot product will help us in interpreting and find the cross product of 3D vectors in our next lesson!

So, together in our video lesson, we will expand upon our knowledge of vectors and discover how to find the Dot Product in 3d, Direction Angles, determine whether or not two vectors are perpendicular (orthogonal), and even learn how to find vector projections.

There’s so much to discover, so let’s get to it!

Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Dot-Product-3D-Example

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.

4.9 / 5

1,132 Reviews

Kevin S.10-30-24 - CO, United States

I had never even heard of discrete math before I had to take it for my Bachelor's in Cybersecurity. I had actually hoped that my math days were done! I suffered through class not understanding any of the presentations until I stumbled across Calcworkshop. I used the Calcworkshop lessons more than I used my instructor's lectures and my book. I ended up with a high B (just 12 points away from an A) thanks to Jenn. Without her easy to understand style of teaching, I'm not sure I would have even passed the class. Thank you so much!!!

Serafimk2203-28-25 - NJ, United States

I had an Amazing experience with discrete math and calculus series. Graduating with highest honors thanks to calc workshop. I'll be back on the site again but this time if I need to go back as reference as well as if I get rusty in my career.

Maria03-26-25 - AB, Canada

I found Jenn's videos near the end of my discrete math class, so I only had a month to go through all of her discrete math lessons to study for my exam. I'm sure I would have aced it if I had more time but I got a pretty good grade considering I thought I would fail.So happy to be done that class!As advertised, Jenn is very thorough and doesn't skip steps, she lets you know exactly how she gets from a to b or she will refer you to other videos where she teaches the techniques she's using more in depth. This was extremely valuable to me, being a mature student taking advanced math while not remembering basic algebra.And it was fun to understand and solve complex problems vs memorize proof structures.

Robbin03-18-25 - CO, United States

Very well organized, helpful and comprehensive. It is great also to have access to prior course material so you can easily go back and refresh if you need to. Jenn is very clear and the number of examples leaves one comfortable with each topic. Couldn't be happier.

RCJK03-07-25 - ID, United States

I had to take Calculus I and II as accelerated classes while working full time. It was my first time taking this courses and was very overwhelming. Calcworkshop really made learning the subjects easier for me by having all the subjects easy to find and easy to understand explanations. I received a B in both classes which I am extremely happy with doing the classes in double time.

Jacqueline S.03-07-25 - SC, United States

Jenn is awesome!Her breakdown of the topic is beyond what you would expect. She is showing you how to arrive at the answer instead of doing a simple equation. Most people need to know the why it give confidence and structure to the learning process. This is what Jenn is great at, she knows how to deliver the information to a non math mind in a way that instills knowledge that you can forever draw from as you move forward. It's really well thought out. She is a true master teacher. Thanks for all that you do for us! Hugs n Blessings... JS

Jujuana03-05-25 - MO, United States

I love the videos the way each lesson is explained step by step. I love that she has examples that you can go over again and again in order to understand the way algebra works. I was lost because my instructor was flying through each lesson and I was totally lost. I attached my syllabus and they helped me stay focus on what I was working and give me a guide to go back and refresh what I went over in class.

Stacey01-31-25 - AZ, United States

Hello, I highly recommend getting a subscription to Jenn and her Calcworkshop teaching math service. I did a general, "go from bad to good at math", Google search and found out about Calcworkshop through responses to the topic on reddit. I've just started watching her videos and found them to be extremely helpful. I'm going back to college after a long absence and math was never my strong suit. So I'm starting at the very bottom of her available subjects and going from there. Just watching a couple of the videos has taken me from being dragged along not understanding to following along just fine in my math class. I'm moving from the "I'll never get this", to the "I look forward to understanding this", mindset in approaching math. This for me is huge, and even though I have a long way to go, I'm confident I will get there thanks to Jenn. Totally worth it!

Kathy W.01-14-25 - WA, United States

Calcworkshop is an outstanding source to learn math and understanding math concepts. Jenn is an outstanding master teacher. Every lesson is clearly presented making understanding easy to grasp. Practice lessons with accompanying answers are given for each section. I am 82, a retired teacher and lifelong learner. Learning calculus has always been on my bucket list. Calcworkshop is helping me reach my goal.

Cheryl01-14-25 - NY, United States

Calc workshop is the absolutely best resource for math and I have seen almost everything that exists out there. I have even recommended it to my daughter's school so that all the kids could use the videos during the summer months for the subject they plan to study in the fall. They are guaranteed to get a A if they have watched the videos and completed the problems before taking the class. Students who are weak in areas can access lower level classes and those who seek to advance above grade level can do so. The videos and exercises are crystal clear and the excellent presentations raise the bar for teachers everywhere. I have always believed that one great math teacher is important in the education process. The videos, exercises and problems are excellent. It is not possible to have ANY knowledge gaps. I have never seen anything on the market that even begins to compete with it!

Justin N.12-22-24 - OK, United States

Calculus can be a scary subject. I know I was scared. I had been out of any math class for over 23 years. I had taken an 8 week Calculus 1 class and felt like I was overloaded. Going into Calculus 2 I found CALCWORKSHOP.com. I used the training videos and material to really dive back into Calc 1 and prepare for Calc 2. Long story short with the material provided and ample study time, I finished Calc 2 with a 95%. Thanks Jenn!

Shelby12-10-24 - OH, United States

CalcWorkshop was a wonderful resource as someone going onto a college calculus 1 class after not having taken a math course in a year! Jenn always explained things in a logical order that built upon previous lessons, and the way she explained topics was always easy to understand. Calcworkshop saved this semester for me, and I couldn't be more grateful to have found this site. :)

Jordan Q.12-09-24 - AR, United States

Anyone struggling with math at any level would greatly benefit from this product. I signed up for it immediately after getting a D on my first exam in calculus 2 and ended up getting A's and B's on the remaining exams, getting a B overall in the class. Jenn breaks down the topics, without skipping any steps, in a way that makes them very easy to understand. I highly recommend this product!

N8Booker11-28-24 - MA, United States

I'm in school to get my degree Networking and Cybersecurity and I'm in my first year. I've been away from school for quite a long time so the concepts that are being taught although not foreign to me, have so much dust on them from a lack of being used in real world applications regularly.I stumbled upon CalcWorkshop by pure chance and it has been a game changer for me. Jen filled in the gaps in between what my Professor is teaching at a rapid fire pace and where my brain grasps and applies it. If not for Jen's approach, I'd have failed my test I took miserably!Am I grateful? It goes beyond words and not I recommend her workshops to everyone!

Kevin S.10-30-24 - CO, United States

Maria03-26-25 - AB, Canada

RCJK03-07-25 - ID, United States

Jacqueline S.03-07-25 - SC, United States

See more reviews on Shopper Approved