Cylindrical and Spherical Coordinates (w/ Examples!)

Have you ever encountered a task or a situation where you didn’t know what to do and needed help?

Jenn (B.S., M.Ed.) of Calcworkshop® teaching cylindrical & spherical coordinates

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

Sometimes looking at something from a different angle or perspective is all we need to set things to rights.

And that is why Cylindrical and Spherical Coordinates are so convenient.

They allow us to look at commonly occurring surfaces and solids from a different point of view — making things easier for us to solve and evaluate such things as volumes and triple integrals.

Okay, so in plane geometry, we use the Cartesian coordinate system where everything is expressed in terms of $x$ , $y$ , or $z$ .

But there are instances when Cartesian coordinates (rectangular coordinates) are too cumbersome or difficult to use, and we need an easier or more helpful way to represent an object.

Two such transformations are the cylindrical and spherical coordinate systems.

Rectangular To Polar Coordinates

But first, let’s remind ourselves of polar coordinates, as they will play a vital role in understanding these two new coordinate systems.

In Polar coordinates, a point in a plane is determined by a radial distance, $r$ , from the origin and the angle $θ$ measured in radians representing the distance from the x-axis.

And we recall, we use the following equations to help us convert back and forth.

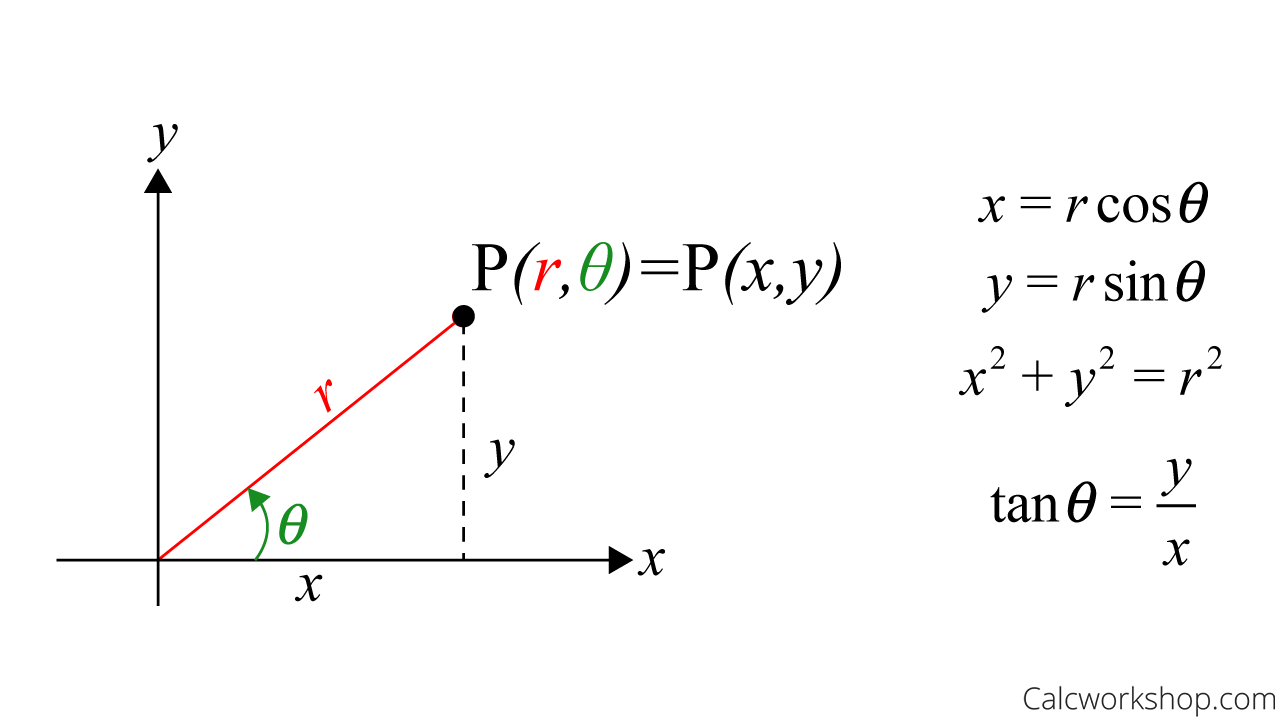
Polar Coordinate To Cartesian

But seeing how polar Coordinates is only for two dimensions, we need to adapt this ever so slightly for three-dimensional space.

Cylindrical Coordinate System

In the cylindrical coordinate system, a point $P$ in three-space is represented by the ordered triple $(r, θ, z)$ where $r$ and $θ$ are polar coordinates of the projection of $P$ onto the xy-plane and $z$ is the directed distance from the xy-plane to point $P$ .

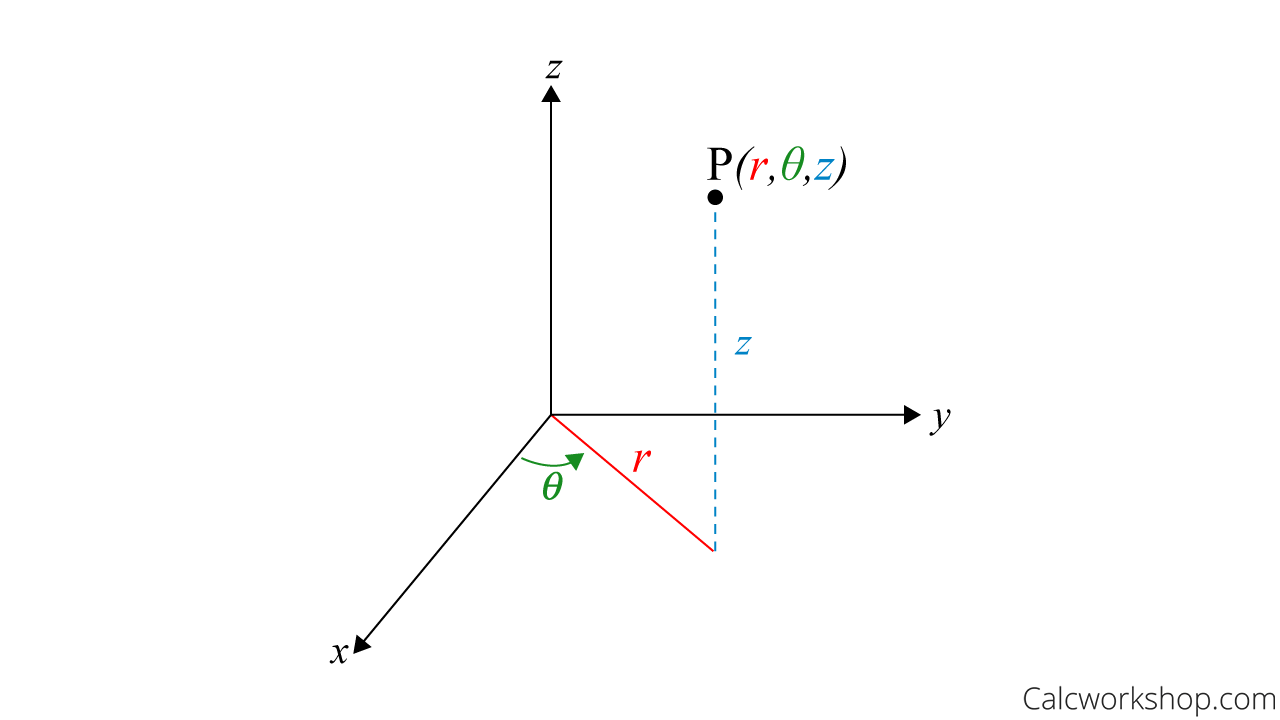
Cylindrical Coordinate System

Notice how Cylindrical Coordinates is just Polar coordinates but with a z-component!

This means, converting back and forth from rectangular coordinates to cylindrical coordinates is just as easy.

$\begin{array}{cc} Cylindrical to Rectangular Coordinates & Rectangular to Cylindrical Coordinates \\ x = r \cos θ & x^{2} + y^{2} = r^{2} \\ y = r \sin θ & \tan θ = \frac{y}{x} \\ z = z & z = z \end{array}$

Cartesian To Cylindrical

Example #1 – Rectangular To Cylindrical Coordinates

For instance, let’s convert the rectangular coordinate $(2, 2, - 1)$ to cylindrical coordinates.

Our goal is to change every $x$ and $y$ into $r$ and $θ$ , while keeping the z-component the same, such that $(x, y, z) \Leftrightarrow (r, θ, z)$ .

So, first let’s find our $r$ component by using $x^{2} + y^{2} = r^{2}$ .

$(2, 2, - 1) \Rightarrow x^{2} + y^{2} = r^{2}$

$\begin{matrix} (2)^{2} + (2)^{2} = r^{2} \\ 8 = r^{2} \\ r = \sqrt{8} = 2 \sqrt{2} \end{matrix}$

Next, we will find $θ$ by using $\tan θ = \frac{y}{x}$ .

$(2, 2, - 1) \Rightarrow \tan θ = \frac{y}{x}$

$\begin{matrix} \tan θ = \frac{2}{2} \\ θ = \tan^{- 1} (1) \\ θ = \frac{π}{4} \end{matrix}$

Therefore, the rectangular coordinate $(2, 2, - 1)$ can be written in cylindrical coordinates as:

$(2 \sqrt{2}, \frac{π}{4}, - 1)$

Example #2 – Cylindrical To Rectangular Coordinates

Now let’s look at a problem where we wish to find a rectangular equation for a surface whose cylindrical equation is given as $z^{2} = 1 - 5 r^{2}$ .

Our goal is to change every $r$ and $θ$ into $x$ and $y$ , while once again, keeping the z-variable untouched.

Because we know that $x^{2} + y^{2} = r^{2}$ we can make a direct substitution.

$\begin{aligned} z^{2} = 1 - 5 r^{2} \\ z^{2} = 1 - 5 (x^{2} + y^{2}) \end{aligned}$

Now, all we have to do is simplify.

$\begin{aligned} z^{2} = 1 - 5 x^{2} - 5 y^{2} \\ 5 x^{2} + 5 y^{2} + z^{2} = 1 \end{aligned}$

So, the ellipsoid written in cylindrical coordinates $z^{2} = 1 - 5 r^{2}$ can be rewritten in rectangular coordinates as:

$5 x^{2} + 5 y^{2} + z^{2} = 1$

Not too bad, right?

Common Surfaces

Together in the video, we will work through numerous examples of transforming rectangular and cylindrical coordinates and equations and quickly identifying common surfaces such as cylinders, planes, and cones.

$\begin{array}{ccc} Cylinder & Plane & Cone \\ x^{2} + y^{2} = r^{2}, z constant & z = a & x^{2} + y^{2} = z^{2} \\ r = a, a constant & θ = a & z = r \end{array}$

Spherical Coordinate System

Now there are times when both Rectangular and Cylindrical coordinates just don’t cut it. For example, when dealing with gravitational or electrical fields spherical symmetry is displayed, and the use of an alternative coordinate system, namely Spherical Coordinates, is preferable.

So, let’s change our perspective once again and discover the intricacies of the Spherical Coordinate System.

Spherical coordinates $(ρ, θ, ϕ)$ describe a point in 3-space where $ρ$ (rho) is the distance from the origin to the point. $θ$ (theta) is the same angle in polar coordinates and is measured in radians representing the distance from the x-axis, and $ϕ$ (phi) is the angle between the positive z-axis and the line from the origin to the point.

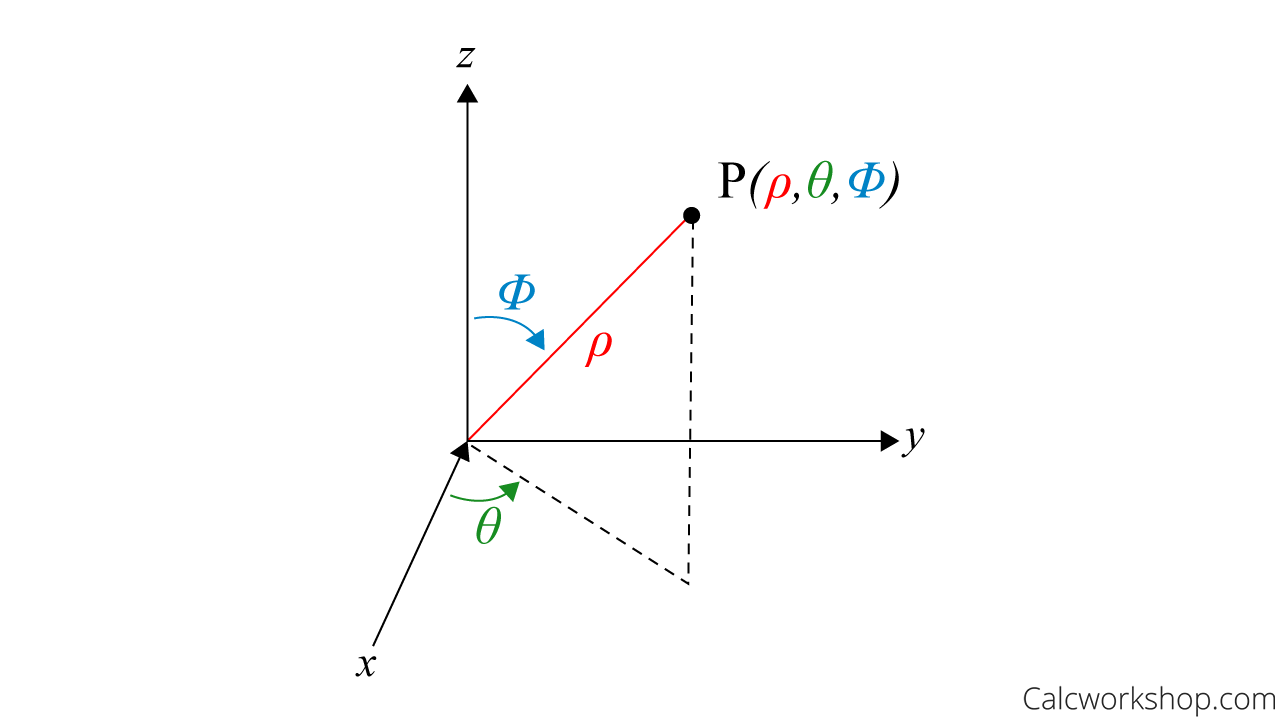
Spherical Coordinate System

It is important to note that $ρ \geq 0 and 0 \leq ϕ \leq π$ .

Cartesian To Spherical

So, how do we convert back and forth from rectangular coordinates to spherical coordinates or from cylindrical coordinates to spherical coordinates?

By using the following formulas:

$\begin{array}{lr} x = ρ \sin ϕ \cos θ & x^{2} + y^{2} + z^{2} = ρ^{2} \\ y = ρ \sin ϕ \sin θ & \tan θ = \frac{y}{x} \\ z = ρ \cos ϕ & \cos ϕ = \frac{z}{ρ} \end{array}$

Example #1 – Rectangular To Spherical Coordinates

Alright, so let’s practice using our equations to convert from rectangular to spherical coordinates.

Suppose we wish to convert the rectangular coordinate $(2, 2, - 1)$ to spherical coordinates. What do we do?

Well, our goal is to change every $x$ , $y$ , and $z$ into $ρ$ , $θ$ , and $ϕ$ , such that $(x, y, z) \Leftrightarrow (ρ, θ, ϕ)$ .

So, first let’s find our $ρ$ component by using $x^{2} + y^{2} + z^{2} = ρ^{2}$ .

$(2, 2, - 1) \Rightarrow x^{2} + y^{2} + z^{2} = ρ^{2}$

$\begin{matrix} (2)^{2} + (2)^{2} + (- 1)^{2} = ρ^{2} \\ 9 = ρ^{2} \\ ρ = \sqrt{9} = 3 \end{matrix}$

Next, we will find $θ$ by using $\tan θ = \frac{y}{x}$ .

$(2, 2, - 1) \Rightarrow \tan θ = \frac{y}{x}$

$\begin{matrix} \tan θ = \frac{2}{2} \\ θ = \tan^{- 1} (1) \\ θ = \frac{π}{4} \end{matrix}$

Lastly, we need to find $ϕ$ by using $\cos ϕ = \frac{z}{ρ}$ and our $ρ$ value we found earlier.

$z = - 1 and ρ = 3 \Rightarrow \cos ϕ = \frac{z}{ρ}$

$\begin{matrix} \cos ϕ = \frac{- 1}{3} \\ ϕ = \cos^{- 1} (\frac{- 1}{3}) \\ ϕ \approx 1.91 radians \end{matrix}$

Therefore, the rectangular coordinate $(2, 2, - 1)$ can be written in spherical coordinates as:

$(3, \frac{π}{4}, 1.91)$

Example #2 – Cylindrical To Spherical Coordinates

Now, let’s look at another example.

If the cylindrical coordinate of a point is $(2, \frac{π}{6}, 2)$ , let’s find the spherical coordinate of the point.

This time our goal is to change every $r$ and $z$ into $ρ$ and $ϕ$ while keeping the $θ$ value the same, such that $(r, θ, z) \Leftrightarrow (ρ, θ, ϕ)$ .

First, we will find our $ρ$ value.

If we know that $x^{2} + y^{2} + z^{2} = ρ^{2}$ , then we can easily say the following.

$\underset{r^{2}}{\underset{⏟}{x^{2} + y^{2}}} + z^{2} = ρ^{2} or r^{2} + z^{2} = ρ^{2}$

Therefore,

$(2, \frac{π}{6}, 2) \Rightarrow r^{2} + z^{2} = ρ^{2}$

$\begin{matrix} (2)^{2} + (2)^{2} = ρ^{2} \\ 8 = ρ^{2} \\ ρ = \sqrt{8} = 2 \sqrt{2} \end{matrix}$

Next, we will calculate $ϕ$ using the equation $\cos ϕ = \frac{z}{ρ}$ , and our recently found $ρ$ .

$z = 2 and ρ = 2 \sqrt{2} \Rightarrow \cos ϕ = \frac{z}{ρ}$

$\begin{matrix} \cos ϕ = \frac{2}{2 \sqrt{2}} \\ ϕ = \cos^{- 1} (\frac{1}{\sqrt{2}}) \\ ϕ = \frac{π}{4} \end{matrix}$

So, the cylindrical coordinate $(2, \frac{π}{6}, 2)$ can be written in spherical coordinates as $(2 \sqrt{2}, \frac{π}{6}, \frac{π}{4})$ .

Awesome!

Common Surfaces

And don’t worry. We will walk through countless examples of how to transform rectangular, cylindrical, and spherical coordinates and easily identify common surfaces such as spheres, half-planes, and half-cones.

$\begin{array}{ccc} Sphere & Half-Plane & Half-Cone \\ ρ = a, a constant & θ = a, a constant & ϕ = a, a constant \end{array}$

There’s a lot to discover, so let’s jump right into the lesson!

Video Tutorial w/ Full Lesson & Detailed Examples (Video)

cylinders-spherical-coordinates-example

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.

4.9 / 5

1,136 Reviews

N8Booker11-28-24 - MA, United States

I'm in school to get my degree Networking and Cybersecurity and I'm in my first year. I've been away from school for quite a long time so the concepts that are being taught although not foreign to me, have so much dust on them from a lack of being used in real world applications regularly.I stumbled upon CalcWorkshop by pure chance and it has been a game changer for me. Jen filled in the gaps in between what my Professor is teaching at a rapid fire pace and where my brain grasps and applies it. If not for Jen's approach, I'd have failed my test I took miserably!Am I grateful? It goes beyond words and not I recommend her workshops to everyone!

Jon, C.04-06-25 - MD, United States

CalcWorkshop is a premier resource for any student seeking to understand, practice, and succeed within the vast areas of mathematics. I am impressed with the quality of instruction and practice problems offered by Jenn. As a engineering student, I always utilize Calcworkshop as a the "first stop" to really understand and gain confidence in the subject. I credit my success in Calculus to Jenn and CalcWorkshop and making me "smarter than the average bear."

Sayida S.04-03-25 - PA, United States

I absolutely love this subscription. At first I was iffy about spending the money, but in the long term it is so worth it. I started watching Jenn almost 3/4ths into my calc 2 class, and I a confidently say I understand the depths to each topic. Before, with my professor I felt that I only understood surface level of each topic. But after the CalcWorkshop videos, I have acronyms, tips, and knowledge I walk away with, that I didn't have before. Genuinely cannot wait to keep using this website for my future endeavors, minoring in Mathematics!

Addie M.04-01-25 - United States

The best resource for improving my math skills and improving my performance in Calculus, as well as through other areas that pertain to other math courses! Jenn is an incredible teacher and I recommend Calcworkshop to anyone who experiences insecurity in math.

Gina K.03-30-25 - WA, United States

My experience was great! I needed help studying for my math class, but I wasn't sure how-until an ad for this popped up on my YouTube. After watching the ad, I was convinced, so I subscribed to CalcWoskop. I'm so happy I did because it helped me so much with my class! I learned a lot that I couldn't grasp from my college lectures, and this was the perfect solution.

Serafimk2203-28-25 - NJ, United States

I had an Amazing experience with discrete math and calculus series. Graduating with highest honors thanks to calc workshop. I'll be back on the site again but this time if I need to go back as reference as well as if I get rusty in my career.

Maria03-26-25 - AB, Canada

I found Jenn's videos near the end of my discrete math class, so I only had a month to go through all of her discrete math lessons to study for my exam. I'm sure I would have aced it if I had more time but I got a pretty good grade considering I thought I would fail.So happy to be done that class!As advertised, Jenn is very thorough and doesn't skip steps, she lets you know exactly how she gets from a to b or she will refer you to other videos where she teaches the techniques she's using more in depth. This was extremely valuable to me, being a mature student taking advanced math while not remembering basic algebra.And it was fun to understand and solve complex problems vs memorize proof structures.

RCJK03-07-25 - ID, United States

I had to take Calculus I and II as accelerated classes while working full time. It was my first time taking this courses and was very overwhelming. Calcworkshop really made learning the subjects easier for me by having all the subjects easy to find and easy to understand explanations. I received a B in both classes which I am extremely happy with doing the classes in double time.

Jacqueline S.03-07-25 - SC, United States

Jenn is awesome!Her breakdown of the topic is beyond what you would expect. She is showing you how to arrive at the answer instead of doing a simple equation. Most people need to know the why it give confidence and structure to the learning process. This is what Jenn is great at, she knows how to deliver the information to a non math mind in a way that instills knowledge that you can forever draw from as you move forward. It's really well thought out. She is a true master teacher. Thanks for all that you do for us! Hugs n Blessings... JS

Jujuana03-05-25 - MO, United States

I love the videos the way each lesson is explained step by step. I love that she has examples that you can go over again and again in order to understand the way algebra works. I was lost because my instructor was flying through each lesson and I was totally lost. I attached my syllabus and they helped me stay focus on what I was working and give me a guide to go back and refresh what I went over in class.

Stacey01-31-25 - AZ, United States

Hello, I highly recommend getting a subscription to Jenn and her Calcworkshop teaching math service. I did a general, "go from bad to good at math", Google search and found out about Calcworkshop through responses to the topic on reddit. I've just started watching her videos and found them to be extremely helpful. I'm going back to college after a long absence and math was never my strong suit. So I'm starting at the very bottom of her available subjects and going from there. Just watching a couple of the videos has taken me from being dragged along not understanding to following along just fine in my math class. I'm moving from the "I'll never get this", to the "I look forward to understanding this", mindset in approaching math. This for me is huge, and even though I have a long way to go, I'm confident I will get there thanks to Jenn. Totally worth it!

Kathy W.01-14-25 - WA, United States

Calcworkshop is an outstanding source to learn math and understanding math concepts. Jenn is an outstanding master teacher. Every lesson is clearly presented making understanding easy to grasp. Practice lessons with accompanying answers are given for each section. I am 82, a retired teacher and lifelong learner. Learning calculus has always been on my bucket list. Calcworkshop is helping me reach my goal.

Cheryl01-14-25 - NY, United States

Calc workshop is the absolutely best resource for math and I have seen almost everything that exists out there. I have even recommended it to my daughter's school so that all the kids could use the videos during the summer months for the subject they plan to study in the fall. They are guaranteed to get a A if they have watched the videos and completed the problems before taking the class. Students who are weak in areas can access lower level classes and those who seek to advance above grade level can do so. The videos and exercises are crystal clear and the excellent presentations raise the bar for teachers everywhere. I have always believed that one great math teacher is important in the education process. The videos, exercises and problems are excellent. It is not possible to have ANY knowledge gaps. I have never seen anything on the market that even begins to compete with it!

Justin N.12-22-24 - OK, United States

Calculus can be a scary subject. I know I was scared. I had been out of any math class for over 23 years. I had taken an 8 week Calculus 1 class and felt like I was overloaded. Going into Calculus 2 I found CALCWORKSHOP.com. I used the training videos and material to really dive back into Calc 1 and prepare for Calc 2. Long story short with the material provided and ample study time, I finished Calc 2 with a 95%. Thanks Jenn!

Shelby12-10-24 - OH, United States

CalcWorkshop was a wonderful resource as someone going onto a college calculus 1 class after not having taken a math course in a year! Jenn always explained things in a logical order that built upon previous lessons, and the way she explained topics was always easy to understand. Calcworkshop saved this semester for me, and I couldn't be more grateful to have found this site. :)

Jordan Q.12-09-24 - AR, United States

Anyone struggling with math at any level would greatly benefit from this product. I signed up for it immediately after getting a D on my first exam in calculus 2 and ended up getting A's and B's on the remaining exams, getting a B overall in the class. Jenn breaks down the topics, without skipping any steps, in a way that makes them very easy to understand. I highly recommend this product!

N8Booker11-28-24 - MA, United States

Jon, C.04-06-25 - MD, United States

Sayida S.04-03-25 - PA, United States

Gina K.03-30-25 - WA, United States

See more reviews on Shopper Approved