Did you know that every corner in your house is a beautiful display of a Cross-Product?
Yep, it’s true!
When two walls and a ceiling meet or intersect, they come together at a 90-degree angle, which is the exact definition of a cross product!
Cool!
Now in our previous lessons, we learned how to:
- Add and Subtract Vectors
- Multiply by Scalars
- Find the Dot Product
For any of these operations, we didn’t worry too much about their dimensions, but for Cross-Products we’re going to have to be very particular about what kind of vectors we’re dealing with.
To find the Cross-Product of two vectors, we must first ensure that both vectors are three-dimensional vectors.
Another thing we need to be aware of when we are asked to find the Cross-Product is our outcome.
Dot Product vs Cross Product
The significant difference between finding a dot product and cross product is the result. The dot product of any two vectors is a number (scalar), whereas the cross product of any two vectors is a vector.
This is why the cross product is sometimes referred to as the vector product.
How come the Dot Product produces a number but the Cross Product produces a vector?
Well, if you can remember when we discussed dot products, we learned that the result is a number that helps us to find the angle between the two vectors.
The Cross Product finds a vector that is perpendicular (orthogonal) to both vectors.
Just like the ceiling is perpendicular to two walls at the corner!
Cross Product Formula
Given two three-dimensional vectors, then the cross product of these vectors is:

Formula for the Cross Product
Now, you can try to memorize this formula…
… or learn the trick!
What’s the trick?
Find the determinant!
All you have to do is set up a determinant of order 3, where you let the first row represent each axis and the remaining two rows are comprised of the two vectors you wish to find the cross product of.
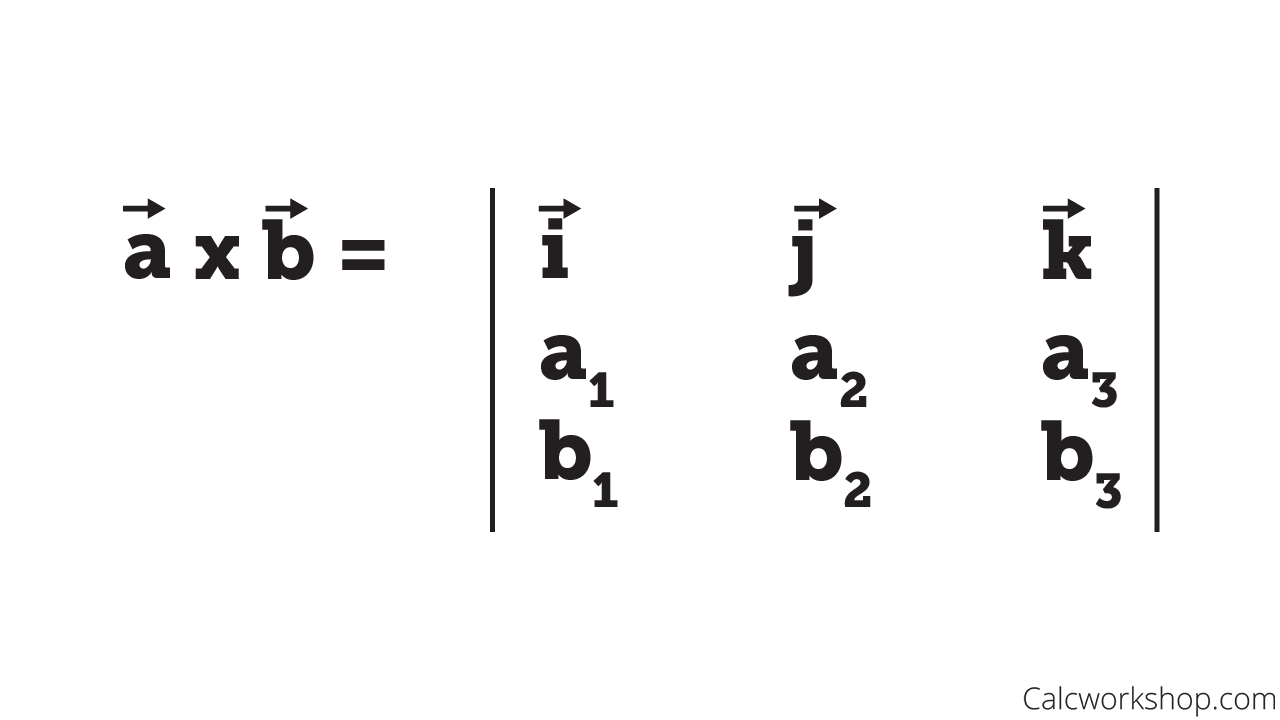
Determinate Rule for Cross Product
Now all that is left is for you to find this 3×3 determinant using the technique of Expansion by Minor by expanding along the top row.
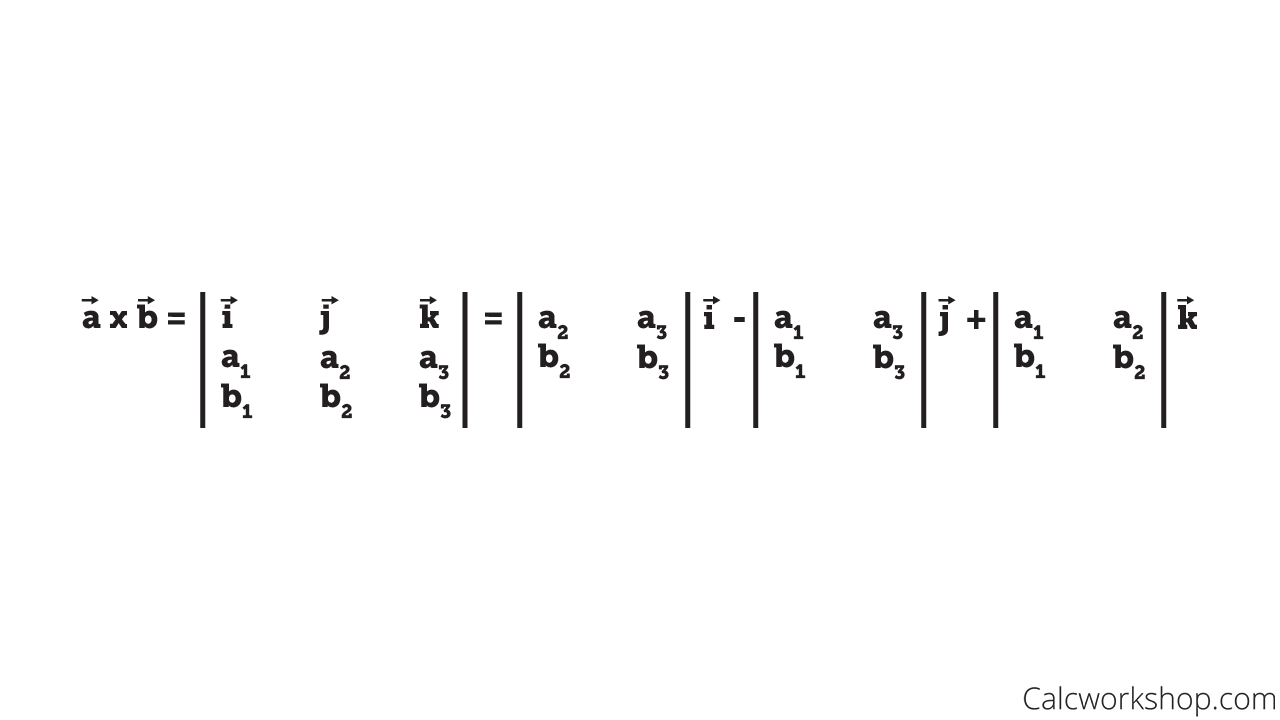
Computing Cross Product via Determinants
Simple!
But now let’s talk about some important rules.
Properties of Cross Products
So we already know the most important property of the cross product, which is the cross product of two vectors is a vector that is orthogonal to the both, as stated by Paul’s Online Notes.
But, if we examine the geometric interpretation of the cross product we discover so much more!

Geometric Interpretation of the Cross Product
And this is precisely how we get the Right-Hand Rule for how to orient our positive and negative directions. The cross product vector of the x and y axes is the z-axis!
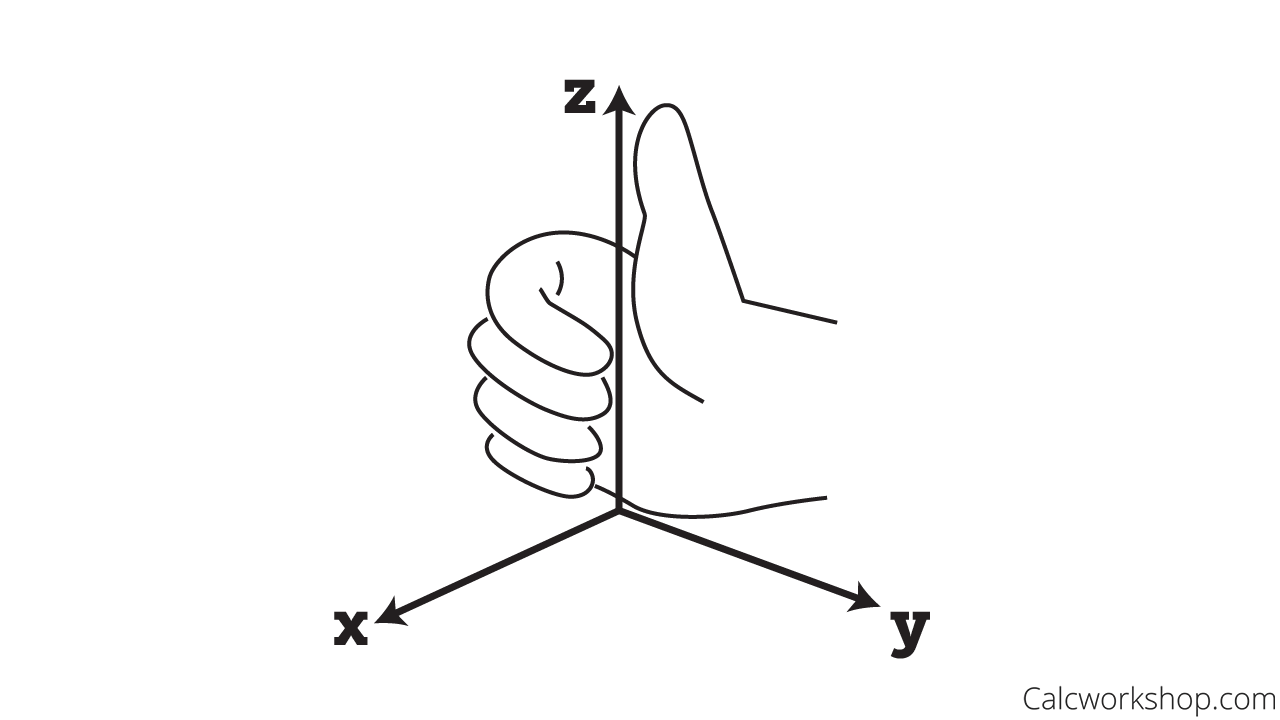
Right Hand Rule for Cross Product
Yay for the Cross-Product!
Also, we can see how the Cross-Product follows the algebraic properties we are so familiar with, such as the Distributive Property, Commutative Property and the Associative Property.

Properties of the Cross Product
Additionally, what this means, according to Oregon State, is that since a vector is completely determined by its magnitude and direction, the cross product of two vectors is a vector that is:
- Perpendicular to both.
- Its orientation is determined by the right-hand rule.
- Its length is equal to the area of the parallelogram determined by both vectors, as seen in the images below.
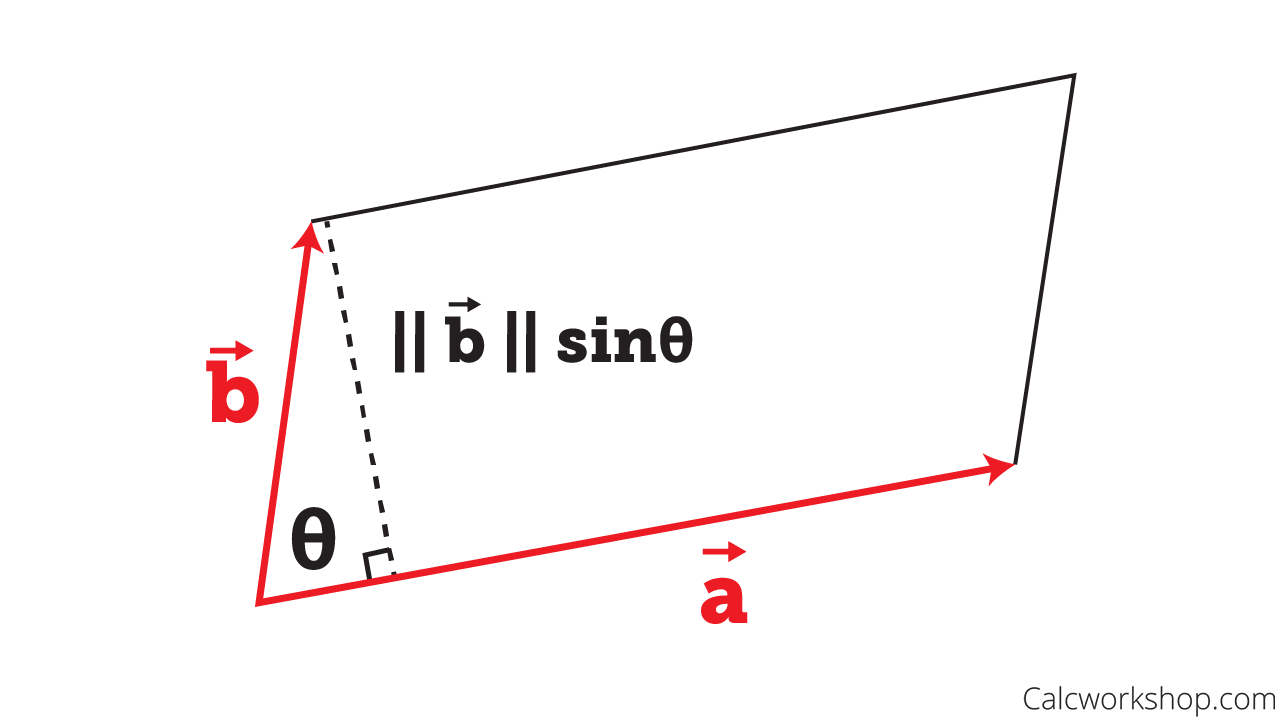
Area of Parallelogram via Cross Product
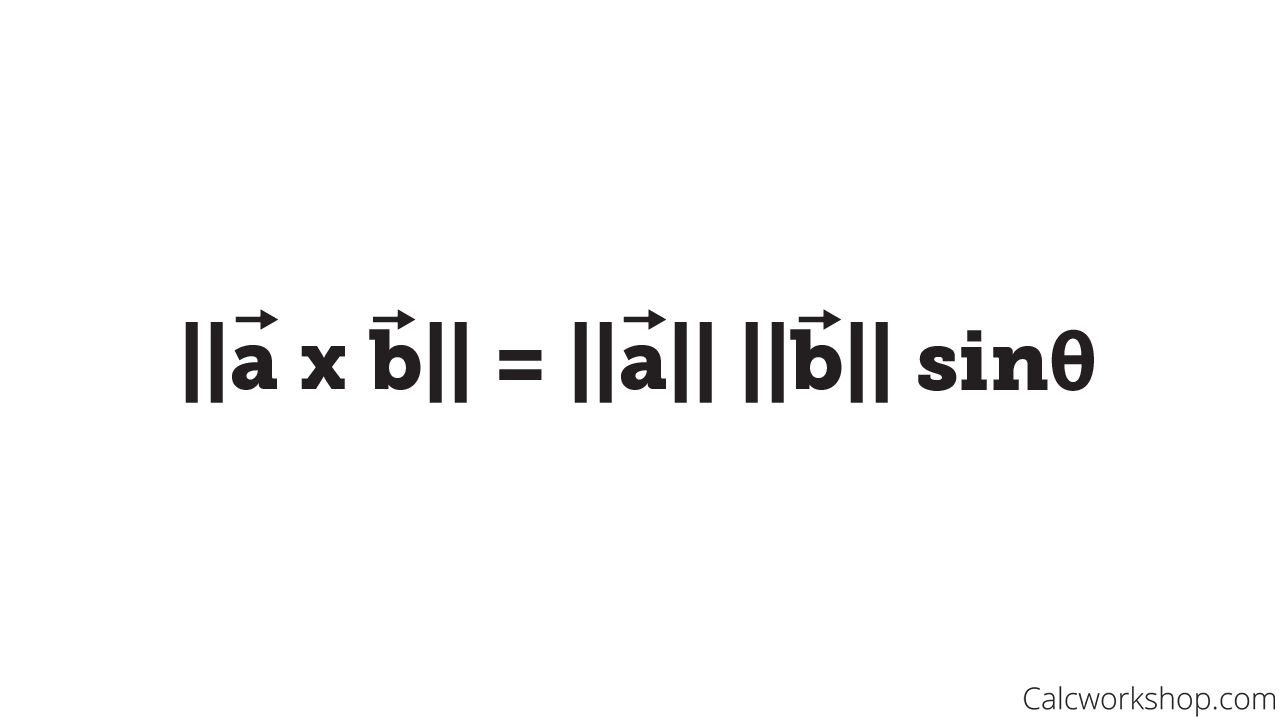
Cross Product Theorem
In this lesson, we will:
- Walk through several cross product examples.
- Determine if two vectors are parallel.
- Learn how to find the area of a parallelogram and the volume of a parallelepiped.
Cross Product Video
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.
