3d vectors you say?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Why are they important…
Because vectors are used in practically everything we see around us.
Vectors are used in many different areas including weather forecasting, GPS tracking, radio transmissions, video games, and vectors are instrumental in the measurement of force, velocity, acceleration, and speed.
The role that vectors play in our everyday lives is immense. Therefore, it’s incumbent upon us to understand and value the use of vectors in 3D space.
What Are Vectors
Alright, so what is a vector?
As we previously learned in precalculus and calculus, a Euclidean vector is a directed line segment with direction and magnitude. In other words, it’s a ray that has a specific direction and length.
A two-dimensional vector is an ordered pair \(\vec{a}=\left\langle a_{1}, a_{2}\right\rangle\) of real numbers, whereas a three-dimensional vector is an ordered triple \(\vec{a}=\left\langle a_{1}, a_{2}, a_{3}\right\rangle\) of real numbers. And the numbers \(a_{1}\), \(a_{2}\), and \(a_{3}\) are called the components of \(\vec{a}\).
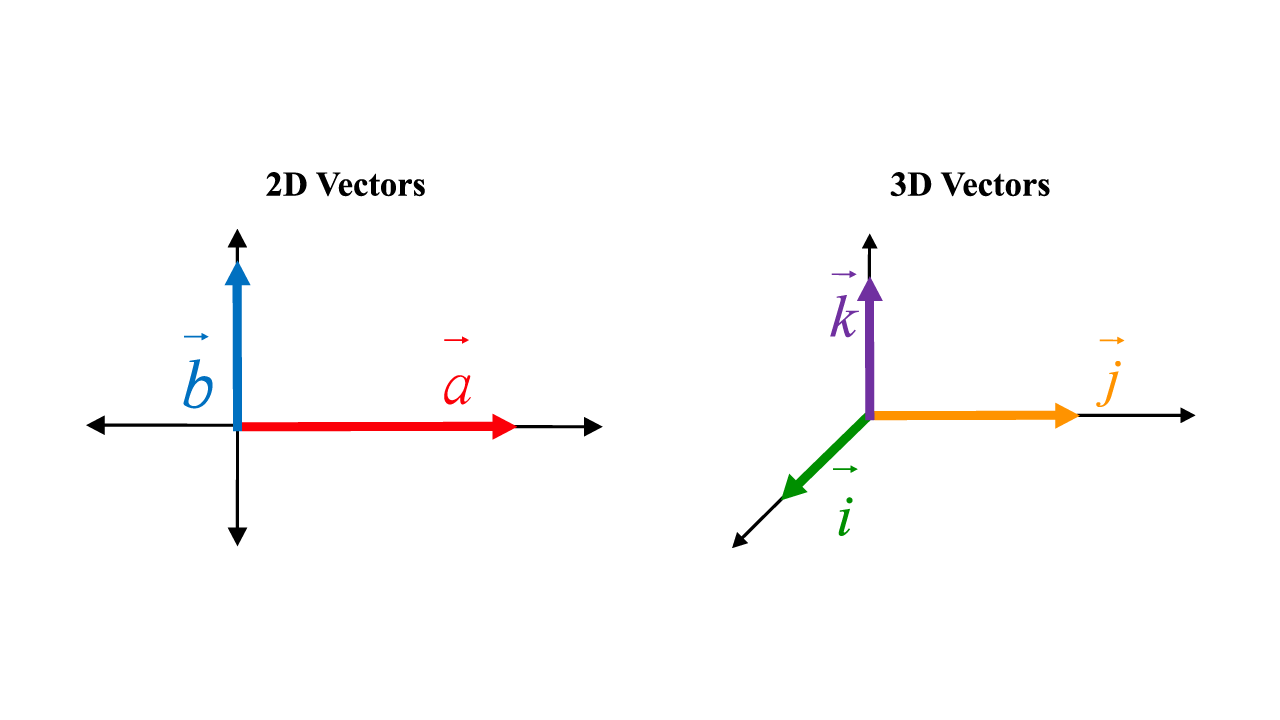
2D Vs 3D Vectors
Additionally, a representation of a vector is a directed line segment from an initial point \(A(x,y,z)\) to a terminal point \(B\left(x+a_{1}, y+a_{2}, z+a_{3}\right)\).
And if the initial point is the origin, then the resulting vector is called the standard position vector.
Finding Vectors
But how do we find a vector representation when all we are given are the initial and terminal points?
It’s simple. All we have to do is subtract their individual components.
Given A\(\left(x_{1}, y_{1}, z_{1}\right)\) and B\(\left(x_{2}, y_{2}, z_{2}\right)\) then vector \(\overrightarrow{A B}=\left\langle x_{2}-x_{1}, y_{2}-y_{1}, z_{2}-z_{1}\right\rangle\).
And to find the length (magnitude) of a 3D vector, we simply extend the distance formula and the Pythagorean Theorem.
Given \(\vec{a}=\left\langle a_{1}, a_{2}, a_{3}\right\rangle\), the length of vector \(\vec{a}\), denoted \(\|\vec{a}\|\) is \(\|\vec{a}\|=\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}\).
Please note that most textbooks will use single, parallel bars when indicating magnitude. This is done when a vector is represented as a bolded letter, such as \(|\boldsymbol{a}|\).
However, this can be very confusing to differentiate between absolute value and magnitude.
To ensure that you can tell the difference, I will always use the double bars to indicate magnitude!
Example – How To Find Position Vectors
Alright, so now let’s look at an example together.
Suppose we wish to find the position vector corresponding to \(\overrightarrow{A B}\) with A(2,-4,3) and B(4,7,-3) and determine its magnitude.
First, we find the position vector by subtracting components.
\begin{equation}
\overrightarrow{A B}=\langle 4-2,7-(-4),-3-3\rangle=\langle 2,11,-6\rangle
\end{equation}Next, we use the formula above to find the length of our vector.
\begin{equation}
\text { If } \overrightarrow{A B}=\langle 2,11,-6\rangle, \text { then }\|\overrightarrow{A B}\|=\sqrt{(2)^{2}+(11)^{2}+(-6)^{2}}=\sqrt{161}
\end{equation}
Easy, right?!
Scalars And Vectors
Okay, so let’s play around with vectors a bit more and discuss the multiplication or product of a vector by a scalar and also vector addition.
If c is a scalar and \(\vec{a}=\left\langle a_{1}, a_{2}, a_{3}\right\rangle\), then vector c\(\vec{a}\) is defined by c\(\vec{a}=c\left\langle a_{1}, a_{2}, a_{3}\right\rangle=\left\langle c a_{1}, c a_{2}, c a_{3}\right\rangle\).
How To Add Vectors
Adding vectors is nothing more than adding corresponding components of two vectors.
If \(\vec{a}=\left\langle a_{1}, a_{2}, a_{3}\right\rangle\) and \(\vec{b}=\left\langle b_{1}, b_{2}, b_{3}\right\rangle\) then the vector \(\vec{a}+\vec{b}\) is defined by:
\begin{equation}
\vec{a}+\vec{b}=\left\langle a_{1}, a_{2}, a_{3}\right\rangle+\left\langle b_{1}, b_{2}, b_{3}\right\rangle=\left\langle a_{1}+b_{1}, a_{2}+b_{2}, a_{3}+b_{3}\right\rangle
\end{equation}
Vector Addition
While this is easy enough, what does this visually look like?
The definition of vector addition is sometimes called the Triangle Law or the Parallelogram Law.
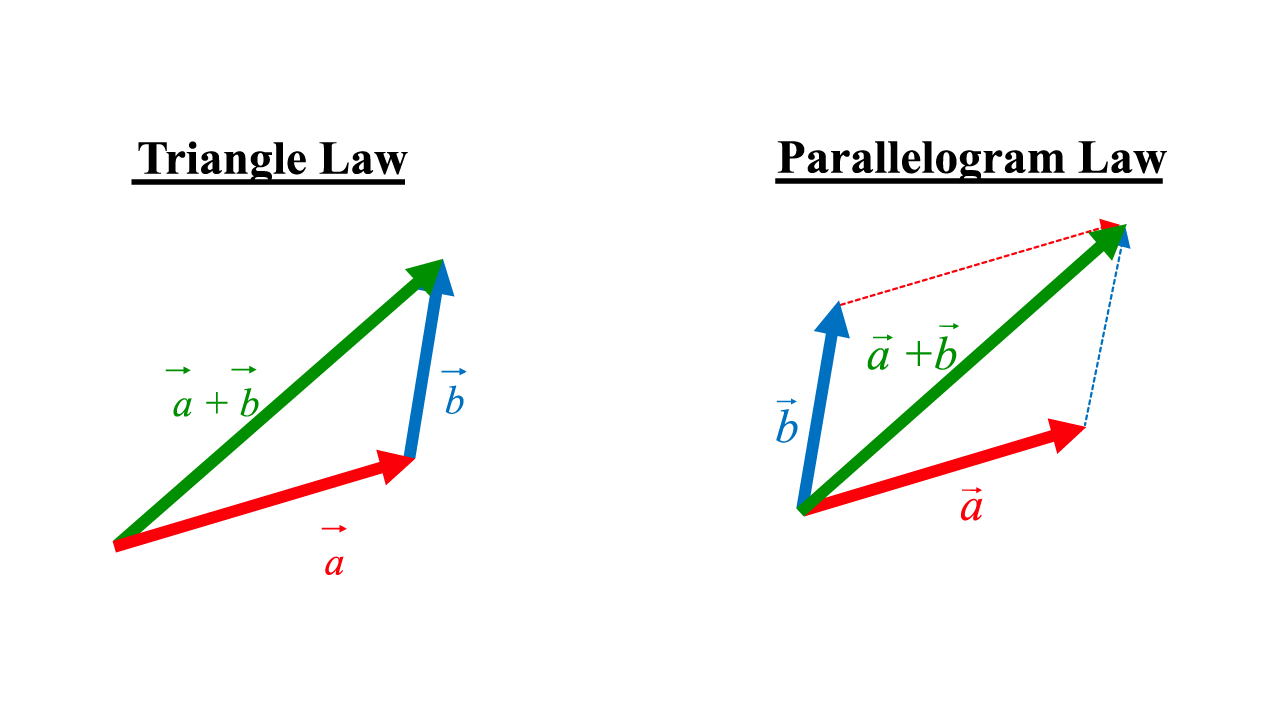
Triangle Law & Parallelogram Law (Vector Addition)
Note that both methods provide the same resultant vector or resultant force, as we will see in our video lesson.
Unit and Zero Vectors
Now it’s time to talk about two important vectors that we will use continuously throughout our course — The zero vector and the Unit vector.
The zero vector is the only vector with a length of 0 and has no specific direction. We denote the zero vector as follows: \(\overrightarrow{0}=\langle 0,0,0\rangle\).
And the unit vector is a vector of length 1, and is denoted \(\vec{u}=\frac{\vec{a}}{\|\vec{a}\|}\).
In general, a unit vector is found by dividing each component of a given vector by its magnitude, which will yield a magnitude of 1 but maintain its direction.
Standard Basis Vectors
And the most famous unit vectors are the standard basis vectors, \(\vec{i}=\langle 1,0,0\rangle\), \(\vec{j}=\langle 0,1,0\rangle\), \(\vec{k}=\langle 0,0,1\rangle\) as they point in the directions of the positive x-,y-, and z-axes and intersect at a 90 degree angle.
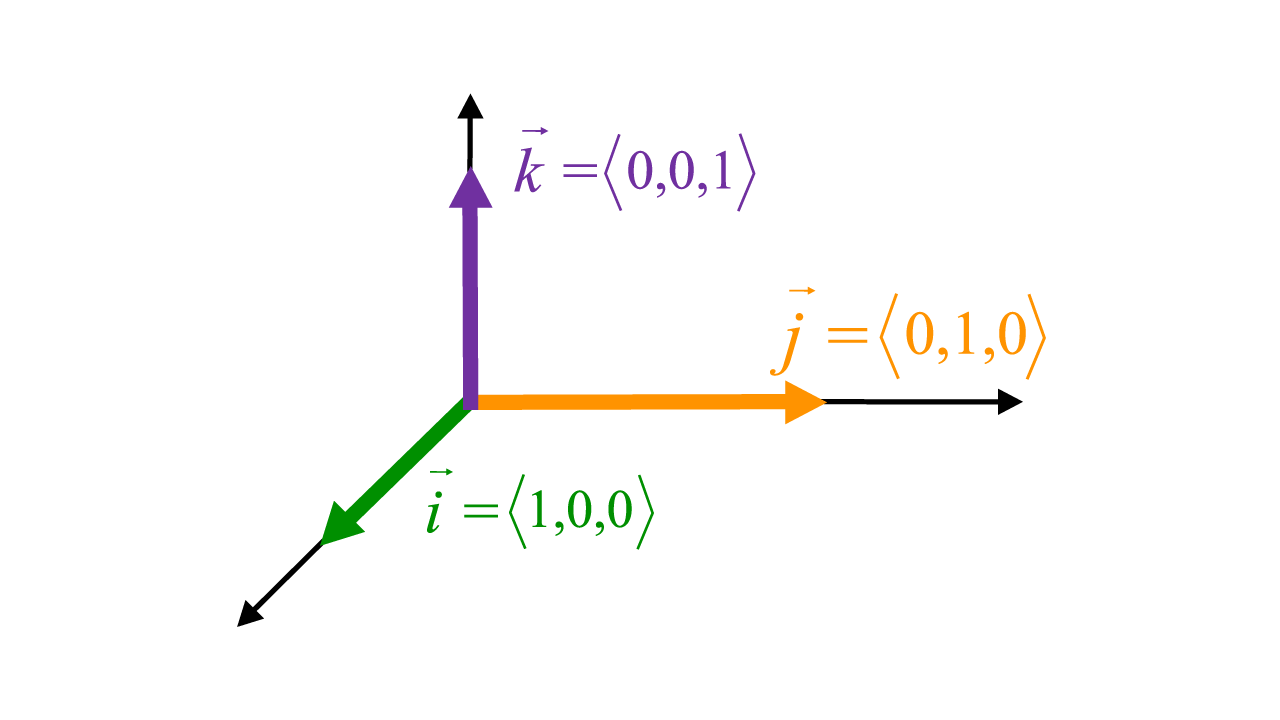
Standard Basis Vectors
Properties Of Vectors
And to complete our review of vectors, it’s now time to discuss the eight basic properties for vectors.
If \(\vec{p}\), \(\vec{q}\), and \(\vec{r}\) are vectors and c and d are scalars, then
\begin{aligned}
\vec{p}+\vec{q} &=\vec{q}+\vec{p} &(\vec{p}+\vec{q})+\vec{r} &=\vec{p}+(\vec{q}+\vec{r}) \\
\vec{p}+\overrightarrow{0} &=\vec{p} & 1 \vec{p} &=\vec{p} \\
c(\vec{p}+\vec{q}) &=c \vec{p}+c \vec{q} &(c+d) \vec{p} &=c \vec{p}+d \vec{p} \\
(c d) \vec{p} &=c(d \vec{p}) & \vec{p}+(-\vec{p}) &=\overrightarrow{0}
\end{aligned}
Notice how similar these rules are to our known Algebraic properties:
- Commutative Property
- Associative Property
- Distributive Property
- Identity Property
- Inverse Property
Cool!
Together we will learn how 3D vectors help us indicate a quantity, such as a velocity and force, and both magnitude and direction. We will discover how to represent and graph a 3D vector in three dimensions, find its magnitude, product of a scalar, add and subtract vectors, create unit vectors and more.
Let’s jump right in and marvel at the importance of vectors.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.