What is the 3D coordinate system?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Great question, and that’s exactly what you’re going to learn in today’s Calculus 3 class.
Let’s go…
Big Idea
The importance of the 3D coordinate system can be seen all around us, and it gives us a way to describe a space.
For example…
- We use a coordinate system to describe an object’s position and location on a map or GPS device.
- Air traffic controllers use coordinates to track aircraft and geographical boundaries and obstacles.
- To show length, width, and height, engineers use a three-dimensional system when designing bridges and buildings.
- And the motion and effects we enjoy in computer animation and video games are all captured using a 3D coordinate system.
3D Coordinate System Defined
We live in a three-dimensional world, so let’s learn how to traverse it using a 3D coordinate system.
First, let’s notice how we divide a plane and space, respectively.
In the 2D Cartesian coordinate system we have only two axes (x-axis and y-axis) that intersect perpendicularly at the origin, whereas in the 3D coordinate system we have three axes (x-axis, y-axis, and z-axis) that all intersect perpendicularly at the origin as seen below.
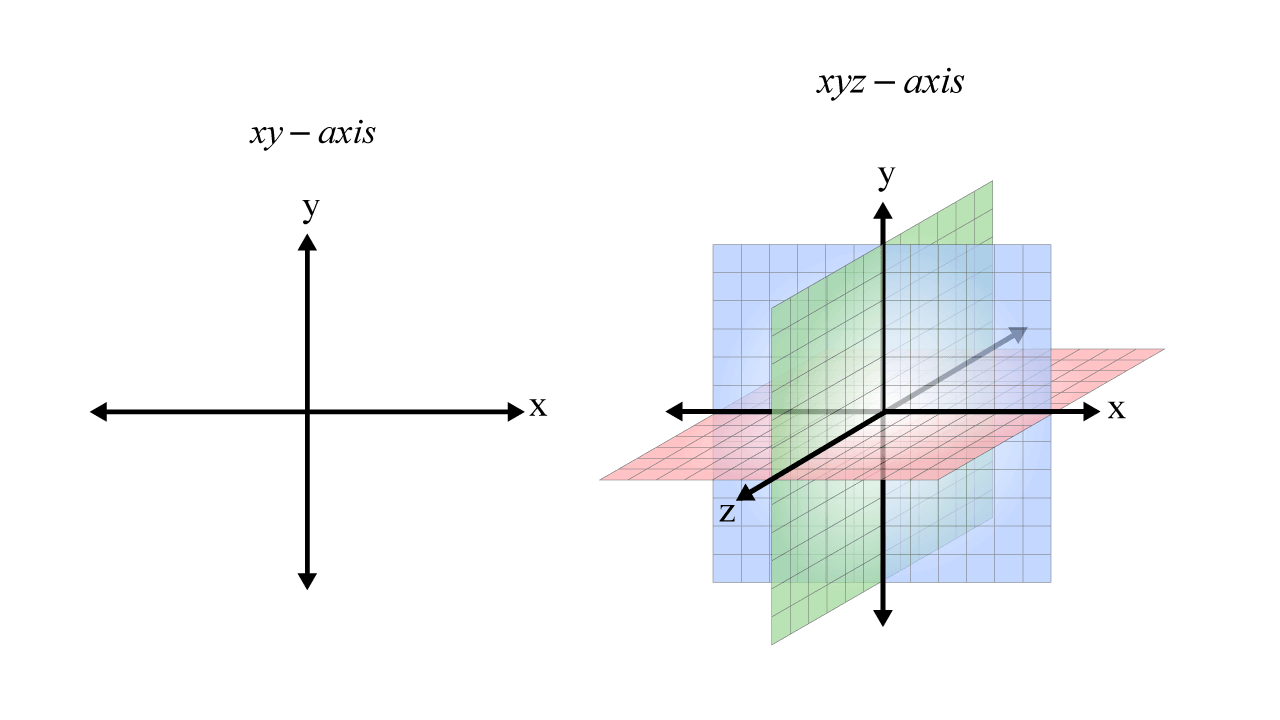
XY Vs XYZ Coordinate Axes
Next, let’s discuss the difference between a point in a plane and a point in space.
A point in a plane uses a two-number system, whereas a point in space requires a three-number system.
Notice how in the 2D coordinate system point \(P\) is represented by an ordered pair (x,y) indicating the horizontal and vertical distance from the origin. In the 3D coordinate system point \(P\) is represented by an ordered triple (x,y,z) indicating the distance along the x-axis, y-axis, and z-axis from the origin.
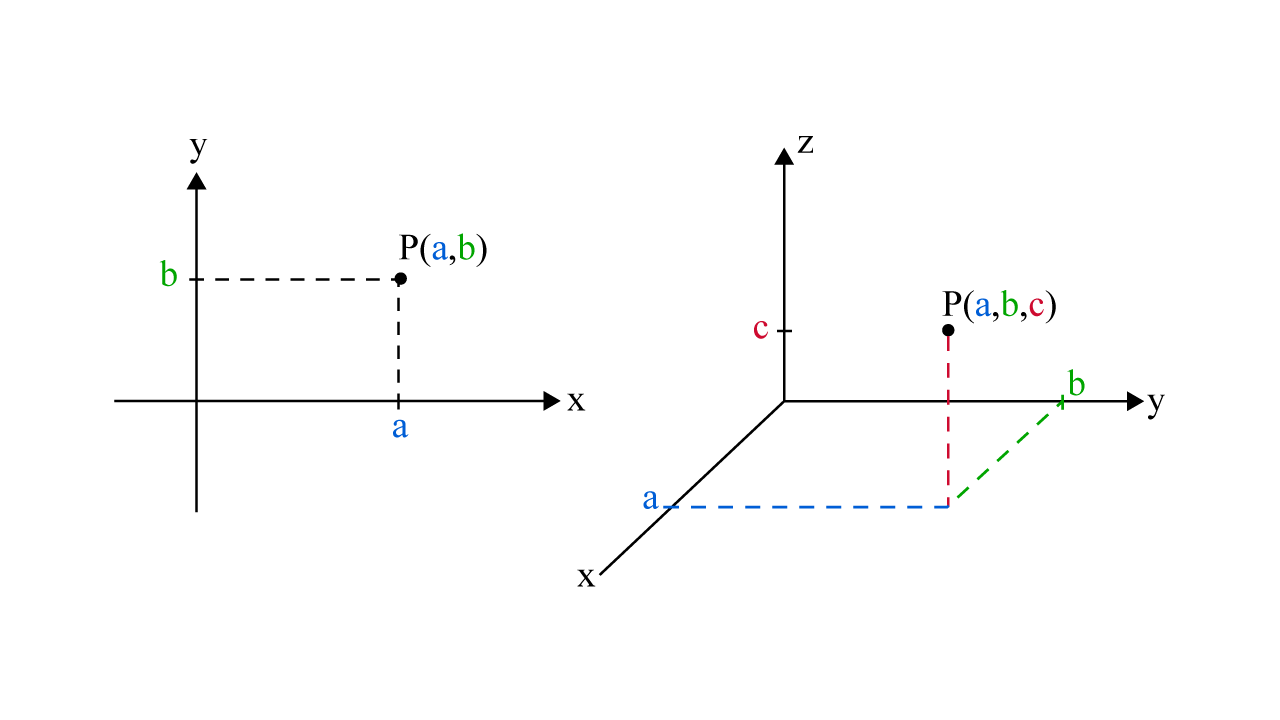
2d vs 3d Coordinate System
Right Hand Rule (XYZ)
But how do we visualize and geometrically represent the 3D coordinate system? Why do we draw the axes the way that we do, with the x- and y-axes acting like the base and the z-axis acting like the height?
The answer is found in the right hand rule.
The right-hand rule determines the direction of the z-axis. If you place your right on along the positive x-axis and curl your fingers toward the positive y-axis, your thumb points in the direction of the positive z-axis.
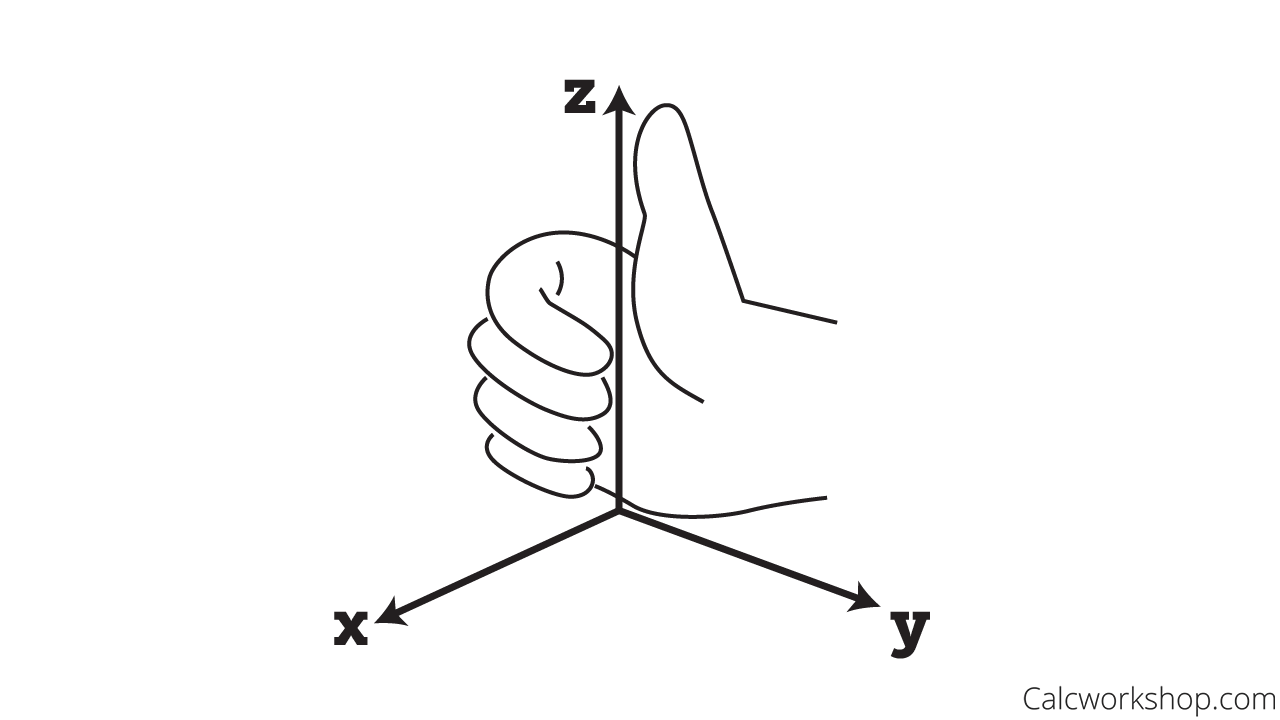
Right Hand Rule
Similarly, we need a new way of distinguishing regions or boundaries in our coordinate system.
In the 2D coordinate system, we have four quadrants, which divide the xy-planes. But in the 3D coordinate system, eight regions divide the xyz-planes. These eight parts are called octants.
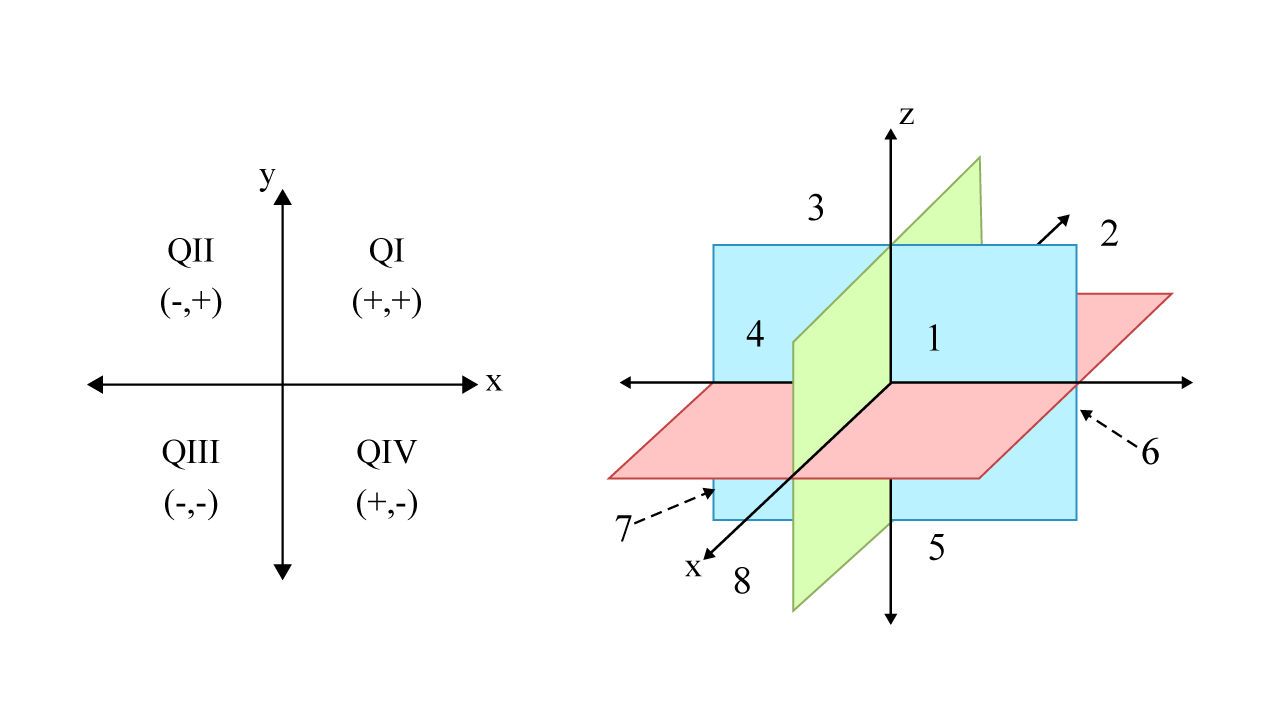
Four Quadrants Vs Eight Octants
Transitioning from 2D to 3D Geometry
Now it’s time to take what we have learned from our 2D system and apply it to our 3D system.
In two-dimensional analytic geometry, the graph of an equation represents a curve in 2-space. But in three-dimensional analytic geometry, an equation represents a surface in 3-space, as seen in the following example.
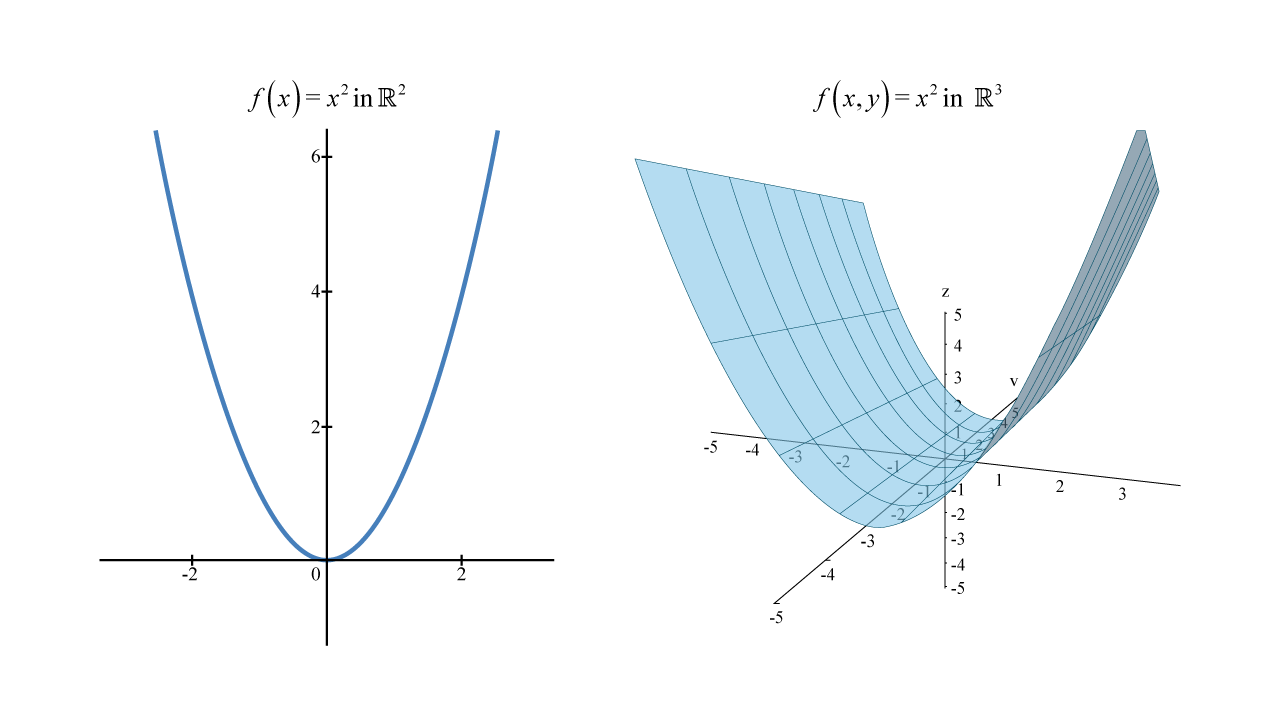
Graphing Equation In 2 Space And 3 Space
Together, we will learn how to describe and sketch in three dimensions and represent the set of all points that define the surface.
Applying Midpoint and Distance Formulas
Additionally, we will review two useful formulas: Midpoint and Distance formulas, and adapt them for three-dimension.
\begin{equation}
\begin{array}{c|c}
\text { Midpoint Formula in } \mathbb{R}^{3} & \text { Distance Formula in } \mathbb{R}^{3} \\
\hline \text { Given points } A\left(x_{1}, y_{1}, z_{1}\right) \text { and } B\left(x_{2}, y_{2}, z_{2}\right), & \text { Given points } A\left(x_{1}, y_{1}, z_{1}\right) \text { and } B\left(x_{2}, y_{2}, z_{2}\right), \\
\text { then the midpoint is } & \text { then the distance between the points is } \\
M=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}, \frac{z_{1}+z_{2}}{2}\right) & D=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}
\end{array}
\end{equation}
These handy formulas will aid us in drawing and finding the equation of surfaces such as cylinders and spheres. And as before, notice how easy it is to take a two-dimensional formula for a circle and transform it into a three-dimensional formula for a sphere.
\begin{equation}
\begin{array}{c|c}
\text { Circle in } \mathbb{R}^{2} & \text { Sphere in } \mathbb{R}^{3} \\
\hline(x-h)^{2}+(y-k)^{2}=r^{2} & (x-h)^{2}+(y-k)^{2}+(z-l)^{2}=r^{2}
\end{array}
\end{equation}
Equations of Spheres in 3D
Now, we shall put all of these formulas to good use with an example.
Let’s find equations of the spheres with a center that touches the
- xy-plane
- yz-plane
- xz-plane
Example – XY-Plane
For a sphere that touches the xy-plane, its radius is the distance from its center to the xy-plane, which is the z-distance of 6.
So, our equation is:
\begin{equation}
\begin{aligned}
&(x-2)^{2}+(y-(-3))^{2}+(z-6)^{2}=(6)^{2} \\
&(x-2)^{2}+(y+3)^{2}+(z-6)^{2}=36
\end{aligned}
\end{equation}
Example 2 – YZ-Plane
For a sphere that touches the yz-plane, its radius is the distance from its center to the yz-plane, which is the x-distance of 2.
So, our equation is:
\begin{equation}
\begin{aligned}
&(x-2)^{2}+(y-(-3))^{2}+(z-6)^{2}=(2)^{2} \\
&(x-2)^{2}+(y+3)^{2}+(z-6)^{2}=4
\end{aligned}
\end{equation}
Example 3 – XZ-Plane
For a sphere that touches the xz-plane, its radius is the distance from its center to the xz-plane, which is the y-distance of 3.
Note that distance is always positive. So, our equation is:
\begin{equation}
\begin{aligned}
&(x-2)^{2}+(y-(-3))^{2}+(z-6)^{2}=(3)^{2} \\
&(x-2)^{2}+(y+3)^{2}+(z-6)^{2}=9
\end{aligned}
\end{equation}
And now, let’s take our knowledge one step further.
Completing the Square in 3D Geometry
Suppose we are given an equation \(x^{2}+y^{2}+z^{2}+4 x-2 y+4 z+5=0\) and wish to verify that the equation represents a sphere.
All we need to do is complete the square and identify the center and radius!
Step 1:
First, we start by grouping all the x’s together, y’s together, and z’s together and moving the constant term to the other side.
\begin{equation}
\begin{aligned}
&x^{2}+y^{2}+z^{2}+4 x-2 y+4 z+5=0 \\
&\left(x^{2}+4 x\right)+\left(y^{2}-2 y\right)+\left(z^{2}+4 z\right)=-5
\end{aligned}
\end{equation}
Step 2:
Now, we complete the square for each group and add those values to the right side.
\begin{equation}
\left(x^{2}+4 x+4\right)+\left(y^{2}-2 y+1\right)+\left(z^{2}+4 z+4\right)=-5+4+1+4
\end{equation}
Step 3:
Next, we factor each group to find our equation in standard form (graphing form).
\begin{equation}
(x+2)^{2}+(y-1)^{2}+(z+2)^{2}=4
\end{equation}
Step 4:
Alright, now we can quickly identify our center and radius.
\begin{equation}
(x+2)^{2}+(y-1)^{2}+(z+2)^{2}=4
\end{equation}
- Center: (-2,1,-2)
- Radius: 2
Ready for More? Join Us in the Video Tutorial
And don’t worry.
- Feeling rusty on completing the square? Discover fun tricks to make it a snap!
- Join us in this video as we tackle multiple examples, mastering how to describe, sketch, and represent surfaces in the 3D coordinate system.
- Together, we’ll apply midpoint and distance formulas, hone essential skills in completing the square, and write equations for cylinders and spheres.
It’s going to be fun, so let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.