Have you ever heard the phrase “efficiency is the key to success”?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Well, good thing we have bases to propel us on our way to success.
Huh?
Bases (basis, singular) is a spanning set with a minimal number of vectors in it; thus, making it a very efficient subspace of a vector space.
Defining a Basis
By definition, if we let \(\mathrm{H}\) be a subspace of a vector space \(\mathrm{V}\) and an indexed set of vectors \(B=\left\{\vec{b}_{1}, \vec{b}_{2}, \ldots, \overrightarrow{b_{p}}\right\}\) in \(\mathrm{V}\) is a basis for \(\mathrm{H}\) if
– \(B\) is a linearly independent set, and
– The subspace spanned by B coincides with \(\mathrm{H}\); that is \(H=\operatorname{Span}\left\{\vec{b}_{1}, \overrightarrow{b_{2}}, \ldots, \overrightarrow{b_{p}}\right\}\)
Consequently, a basis of \(\mathrm{V}\) is a linearly independent set that spans \(\mathrm{V}\).
Finding a Basis for \(\mathbb{R}^{2}\)
Okay, so let’s see if we can make sense of this. Let’s find a basis for \(\mathbb{R}^{2}\)
How?
Well, we need to find two vectors in \(\mathbb{R}^{2}\) that span \(\mathbb{R}^{2}\) and are linearly independent.
Let’s think…
…the columns of the identity matrix just might hold the key.
In \(\mathbb{R}^{2}\) the columns of \(I_{2}\) are:
\begin{aligned}
I_{2} &= \left[\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right] \\
e_{1} &= \left[\begin{array}{l}1 \\ 0\end{array}\right] \\
e_{2} &= \left[\begin{array}{l}0 \\ 1\end{array}\right]
\end{aligned}
And these two columns form the most efficient basis because any vector \(\left[\begin{array}{l}x \\ y\end{array}\right]\) can be written as
\(\left\{\left[\begin{array}{l}1 \\ 0\end{array}\right],\left[\begin{array}{l}0 \\ 1\end{array}\right]\right\}\)
Quite simply:
\begin{aligned}
\left[\begin{array}{l}x \\ y\end{array}\right] &= x\left[\begin{array}{l}1 \\ 0\end{array}\right]+y\left[\begin{array}{l}0 \\ 1\end{array}\right]
\end{aligned}
And nicely verifies the axes of the \(2 D\) plane \(\mathbb{R}^{2}\) .
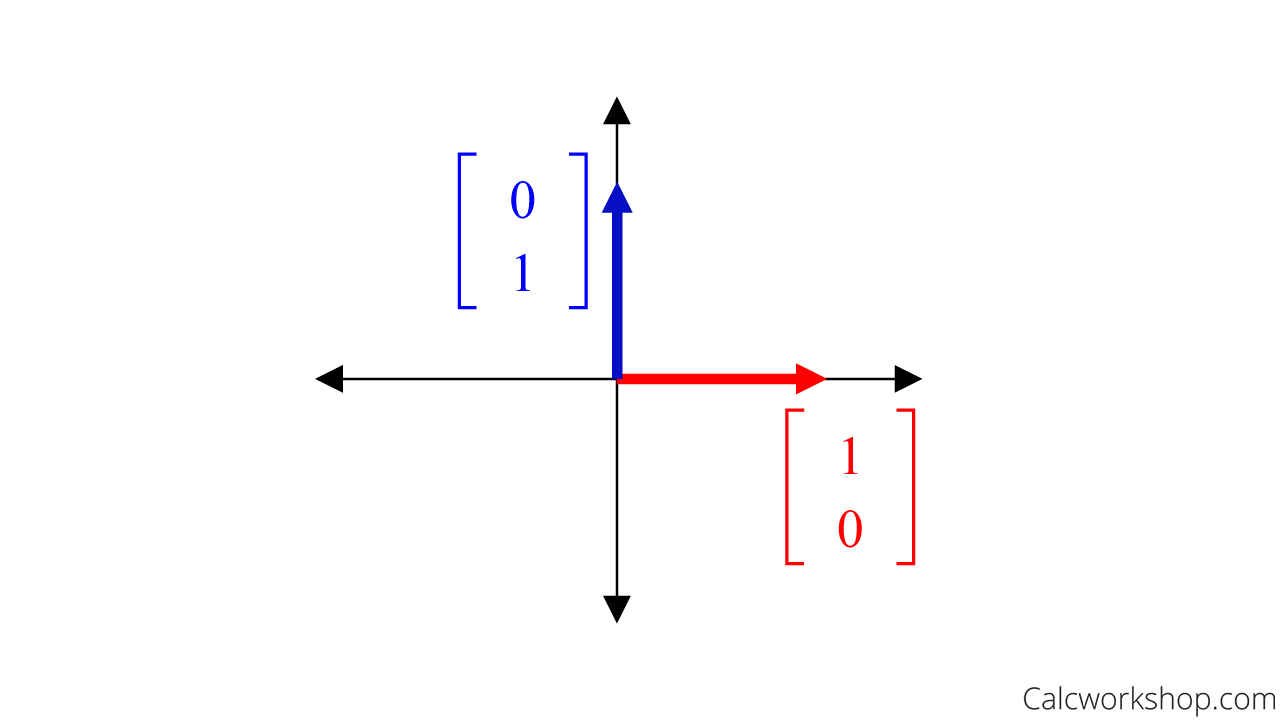
Standard Basis Vectors R2
So, using this information, we can deduce for \(\mathbb{R}^{3}\), the basis would be the columns of the Identity.
Matrix in 3D:
\begin{equation}
\{\underbrace{\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right]}_{e_1}, \underbrace{\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]}_{e_2}, \underbrace{\left[\begin{array}{l}
0 \\
0 \\
1
\end{array}\right]}_{e_3}\}
\end{equation}
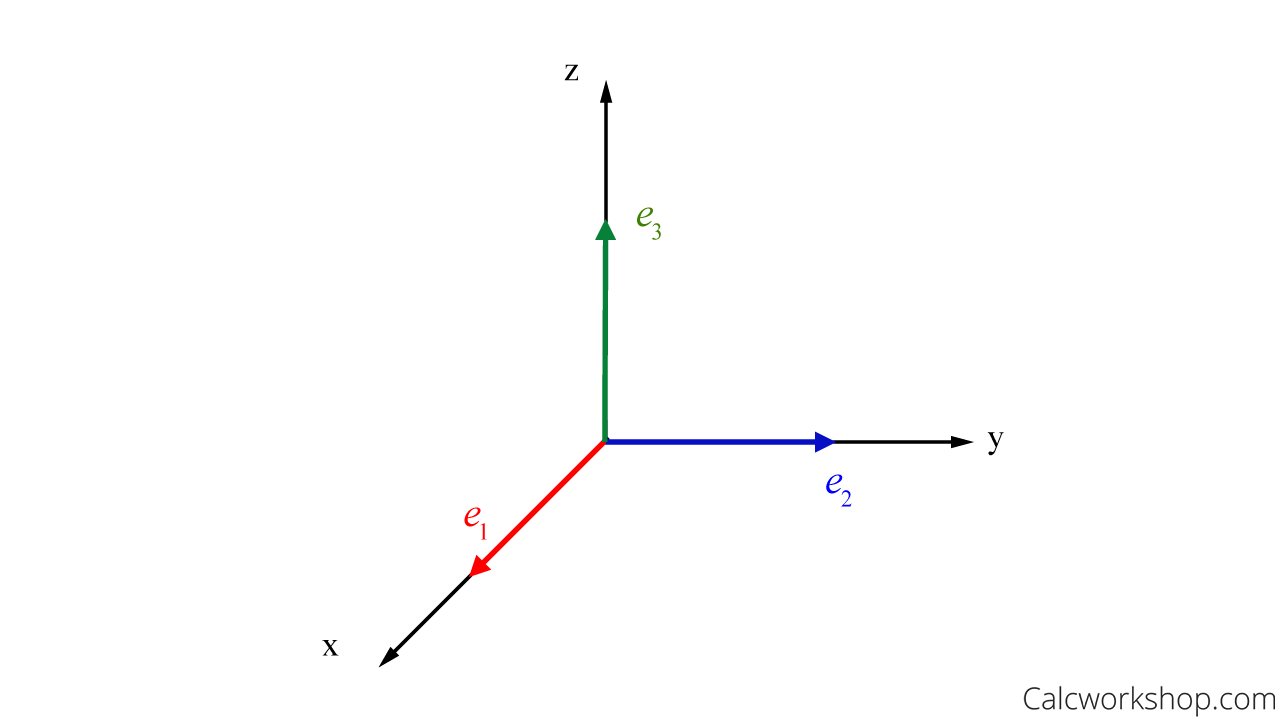
Standard Basis Vectors R3
Therefore, the standard basis for \(\mathbb{R}^{n}\) is the set \(\left\{e_{1}, e_{2}, \ldots, e_{n}\right\}\) where:
\begin{align*}
e_{1}=\left[\begin{array}{c}
1 \\
0 \\
\vdots \\
0
\end{array}\right], e_{2}=\left[\begin{array}{c}
0 \\
1 \\
\vdots \\
0
\end{array}\right], \cdots, e_{n}=\left[\begin{array}{c}
1 \\
\vdots \\
0 \\
1
\end{array}\right]
\end{align*}
Seems easy enough, right?
Identifying Basis for Other Vector Spaces
But now we come to an important question.
How do we determine if a set of vectors, other than the standard basis, form a basis for \(\mathbb{R}^{n}\)?
Well, the Spanning Set Theorem states that if we let \(S=\left\{v_{1}, \ldots, v_{p}\right\}\) be a set in \(V\), and let \(H=\operatorname{Span}\left\{v_{1}, \ldots, v_{p}\right\}\), then.
– If one of the vectors in \(\mathrm{S}\), say \(v_{k}\), is a linear combination of the remaining vectors in \(\mathrm{S}\), then the set formed from \(\mathrm{S}\) by removing \(v_{k}\) still spans \(\mathrm{H}\).
– If \(H \neq\{\overrightarrow{0}\}\), some subset of \(\mathrm{S}\) is a basis for \(H\).
What in the world does this mean?
Since a basis is an “efficient” spanning set that contains no unnecessary vectors, all we have to do is discard the vectors that aren’t needed.
How?
By letting the given vectors form the columns of matrix \(\mathrm{A}\) and determining if matrix \(\mathrm{A}\) is invertible.
This means we look to make sure that none of the vectors are linear combinations of each other.
For example, assume \(v_{1}=\left[\begin{array}{c}0 \\ 2 \\ -1\end{array}\right], v_{2}=\left[\begin{array}{l}2 \\ 2 \\ 0\end{array}\right], v_{3}=\left[\begin{array}{c}6 \\ 16 \\ -5\end{array}\right]\), and \(H=\operatorname{Span}\left\{v_{1}, v_{2}, v_{3}\right\}\). Find the basis for the subspace \(\mathrm{H}\).
There are two methods for solving this problem.
One method is to look for scalar multiple, and the other is to place the columns in a matrix and row reduce to find pivots columns.
Linear Combination Method:
\begin{equation}
5 \underbrace{\left[\begin{array}{c}
0 \\
2 \\
-1
\end{array}\right]}_{v_1}+3 \underbrace{\left[\begin{array}{c}
2 \\
2 \\
0
\end{array}\right]}_{v_2}=\underbrace{\left[\begin{array}{c}
6 \\
16 \\
-5
\end{array}\right]}_{v_3}
\end{equation}
Row Reduction Method:
\begin{equation}
\left[\begin{array}{ccc}
0 & 2 & 6 \\
2 & 2 & 16 \\
-1 & 0 & -5
\end{array}\right] \sim\left[\begin{array}{ccc}
1 & 0 & 5 \\
0 & 1 & 3 \\
0 & 0 & 0
\end{array}\right]
\end{equation}
Our first method shows that \(5 v_{1}+3 v_{2}=v_{3}\) and our second method shows that column \(3\left(v_{3}\right)\) doesn’t contain a pivot.
Consequently, \(v_{3}\) must be discarded leaving the basis for subspace \(\mathrm{H}\) as \(H=\operatorname{Span}\left\{v_{1}, v_{2}\right\}\)
Next Steps
In this video lesson, you will:
- Learn about Linearly Independent Sets and Bases, drawing upon your knowledge of linear independence and the homogeneous equation
- Identify and study subsets that span a vector space \(\mathrm{V}\) or a subspace \(\mathrm{H}\) efficiently
- Define a basis and apply the Spanning Set Theorem
- Discover the connection to the Invertible Matrix Theorem, sometimes referred to as the Square Matrix Theorem
- Review the Null Space and Column Space, and write bases for both
- Examine a set of vectors and polynomial functions to find a basis for the space spanned
Get ready for a fun learning experience, and let’s dive in!
Video Tutorial w/ Full Lesson & Detailed Examples

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.