Let’s quickly review vector calculus and summarize all the higher-dimensional versions of the fundamental theorem of calculus!

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
As quick reminder we have:
- Line Integrals
- Green’s Theorem
- Stokes’ Theorem
- Divergence Theorem
Line Integrals
Given a line integral of a vector field \(\vec F\) over a curve \(C\).
If \(\vec F\) is conservative, then the value of the line integral is the difference between \(f\) evaluated at the initial point and terminal point of the curve where \(\vec F = \nabla f\).
\begin{equation}
\int_{C} \nabla f \cdot d \vec{r}=\int_{a}^{b} \nabla f(\vec{r}(t)) \cdot \vec{r}^{\prime}(t) d t=f(\vec{r}(b))-f(\vec{r}(a))
\end{equation}

Fundamental Theorem Line Integral Geometric Interpretation
Green’s Theorem
Given a line integral of a vector field \(\vec F = \left\langle {P,Q} \right\rangle \) over a closed planar curve \(C\). (Oriented Counterclockwise)
The line integral is equal to the double integral of \(\frac{{\partial Q}}{{\partial x}} – \frac{{\partial P}}{{\partial y}}\) over the planar region bounded by \(C\).
\begin{equation}
\int_{C} P d x+Q d y=\iint_{D}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d A
\end{equation}
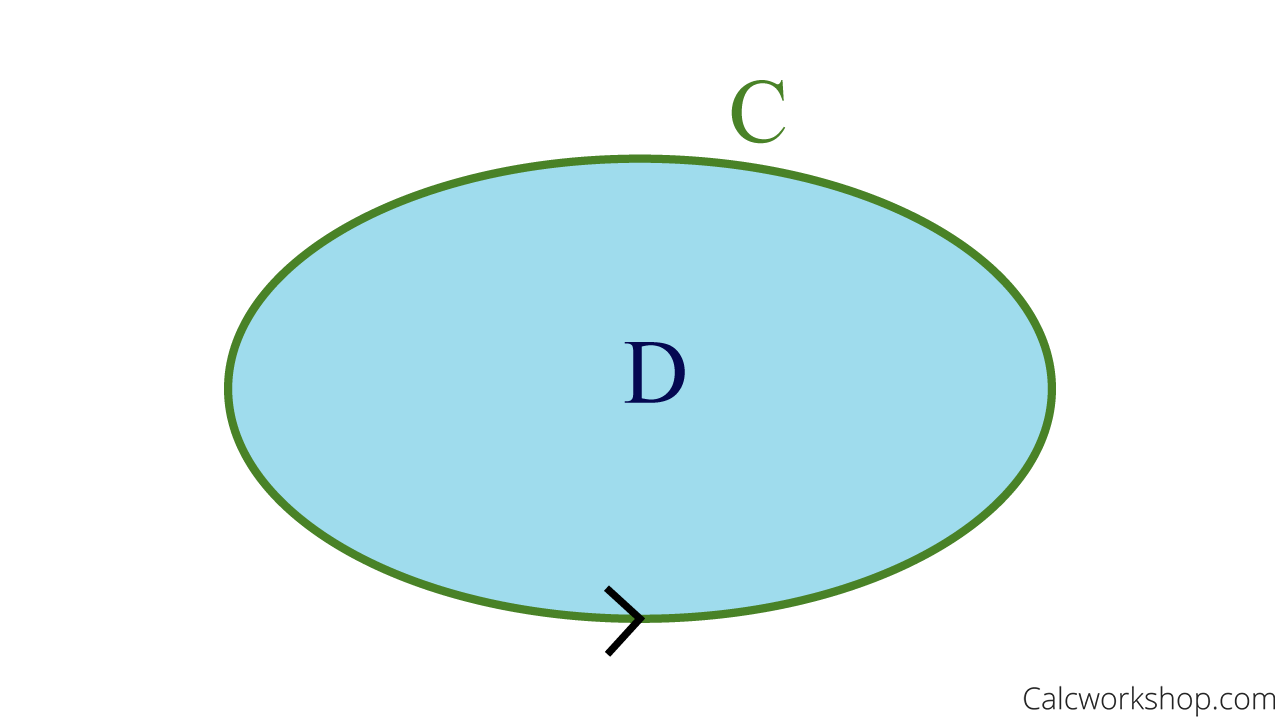
Greens Theorem Geometric Representation
Stokes’ Theorem
Given a line integral of a vector field \(\vec F\) along a curve \(C\).
If the curve \(C\) is closed, then the line integral is equal to the surface integral of \(\nabla \times \vec F\) over any orientable surface that has curve \(C\) as its boundary.
\begin{equation}
\iint_{S}(\nabla \times \vec{F}) \cdot d \vec{S}=\iint_{S} \operatorname{curl} \vec{F} \cdot d \vec{S}=\int_{C} \vec{F} \cdot d \vec{r}
\end{equation}
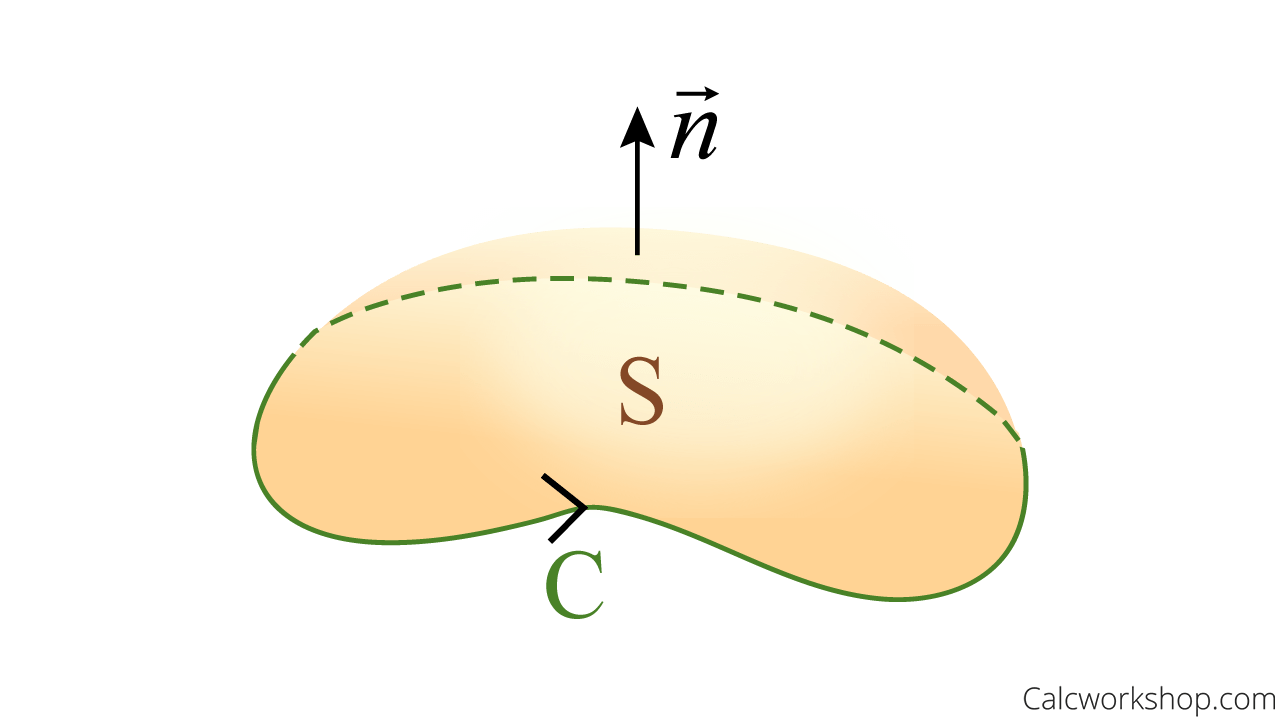
Stokes Theorem Geometric Interpretation
Divergence Theorem
Given a surface integral of a vector field \(\vec F\) over a surface \(S\).
If the surface is closed, then the surface integral is equal to the triple integral of \({\rm{div}}\vec F\) over the region bounded by the surface (\(S\) is the boundary of the solid \(E\)).
\begin{equation}
\iint_{S} \vec{F} \cdot d \vec{S}=\iiint_{E} \operatorname{div} \vec{F} d V
\end{equation}
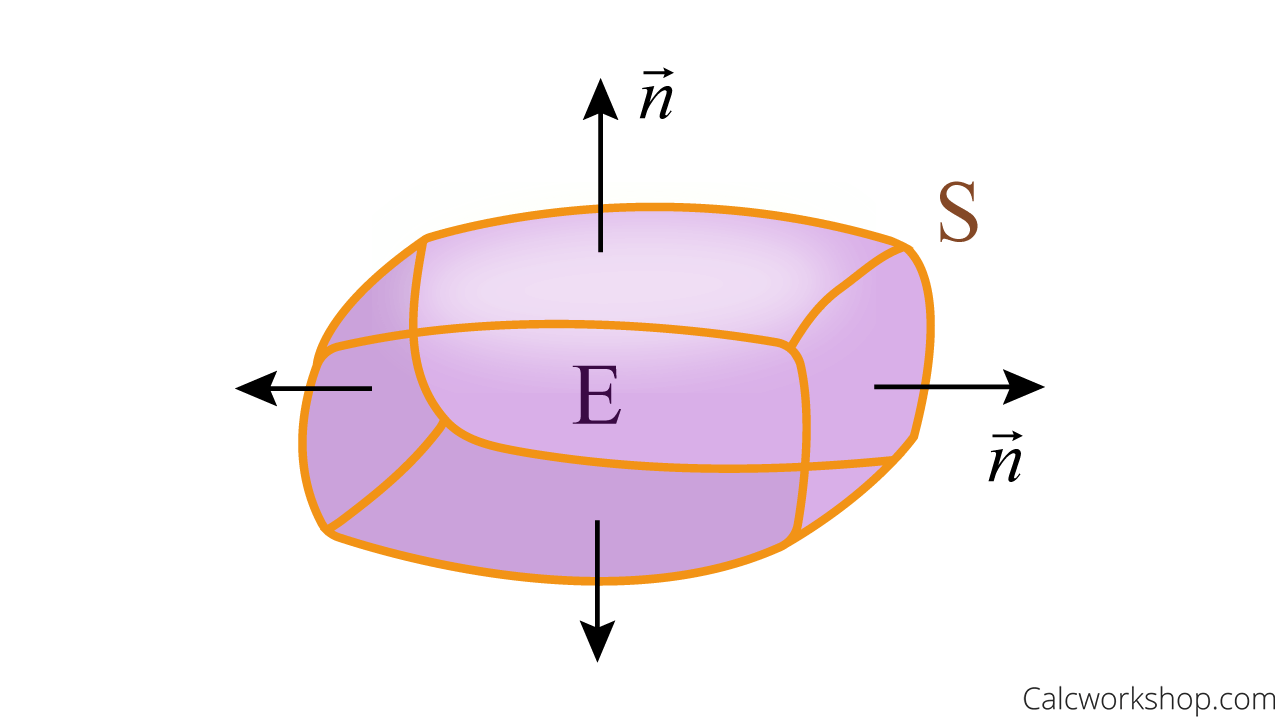
Divergence Theorem Geometric Interpretation
Wow!
Look at everything we’ve learned in this unit!
So, together we will review line integrals and discuss how this is simply an integral evaluated along a curve.
We will review the basic formulas associated with line integrals and discuss how to determine if a vector field is conservative or independent of path.
Then, we will review Green’s theorem and see how this could relate line integrals to double integrals over simple, closed boundary curves.
Next, we will discuss how Green’s theorem helped us find surface integrals for functions and vector fields (flux integral).
Likewise, we will talk about Stokes’ theorem and how it is a higher dimensional version of Green’s theorem and calculates the total microscopic circulation (curl) within a surface. We will be able to determine the net flow of the fluid over a period of time.
And finally, we will review the divergence theorem and see how we can change a surface integral into a triple integral to evaluate the outward flux of a surface.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.