You encounter the word angle all the time, not just in your math classes! As a soccer player, you want to create the best angle for a shot on goal. As an audience member, you want to have the best angle to view a performance. Not to mention the pilot coming in for a landing at the optimal angle for comfort and safety.

In this lesson, we will take a deep dive into angles, more specifically, coterminal angles.
Angle Definition
But let’s not get ahead of ourselves! Let’s start with a look at the definition of an angle.
In geometry, we learned that an angle is formed when two rays are connected at a common endpoint called a vertex.
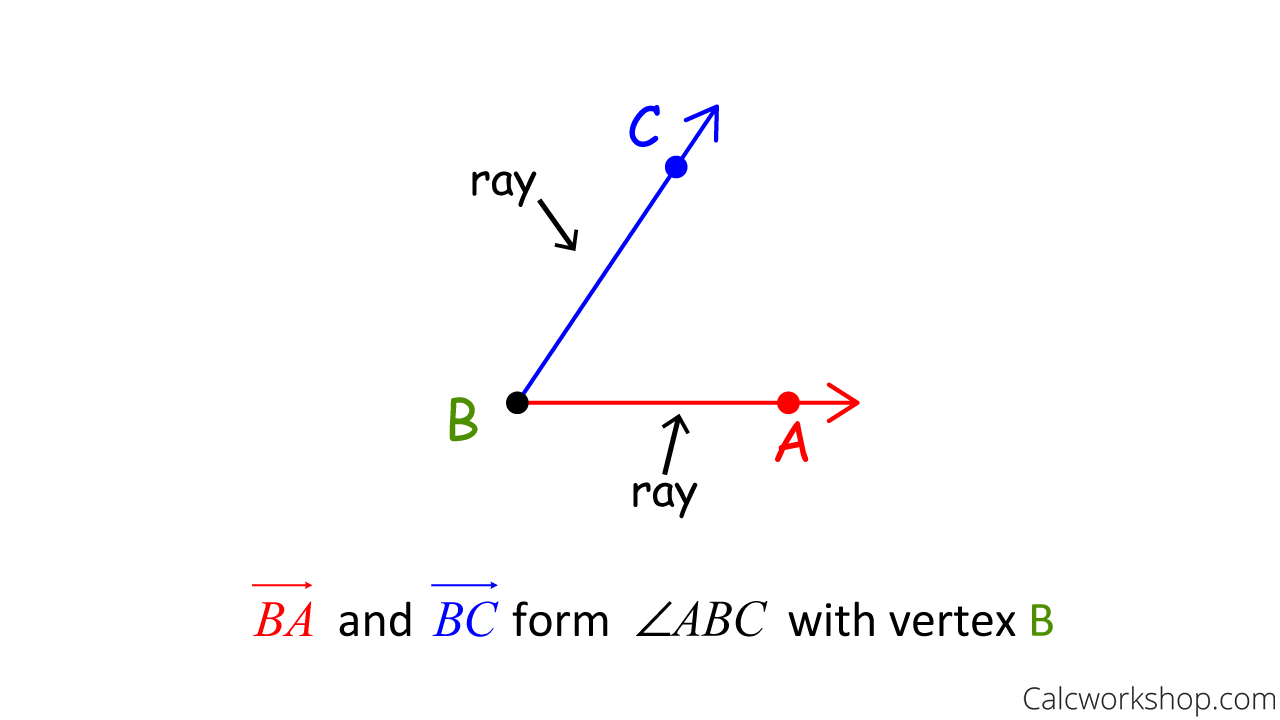
Vertex Of An Angle
But is this the only definition of an angle?
Of course not!
In trigonometry, an angle is formed by the rotation of a ray about its endpoint from an initial (starting) position to a terminal (stopping) position.
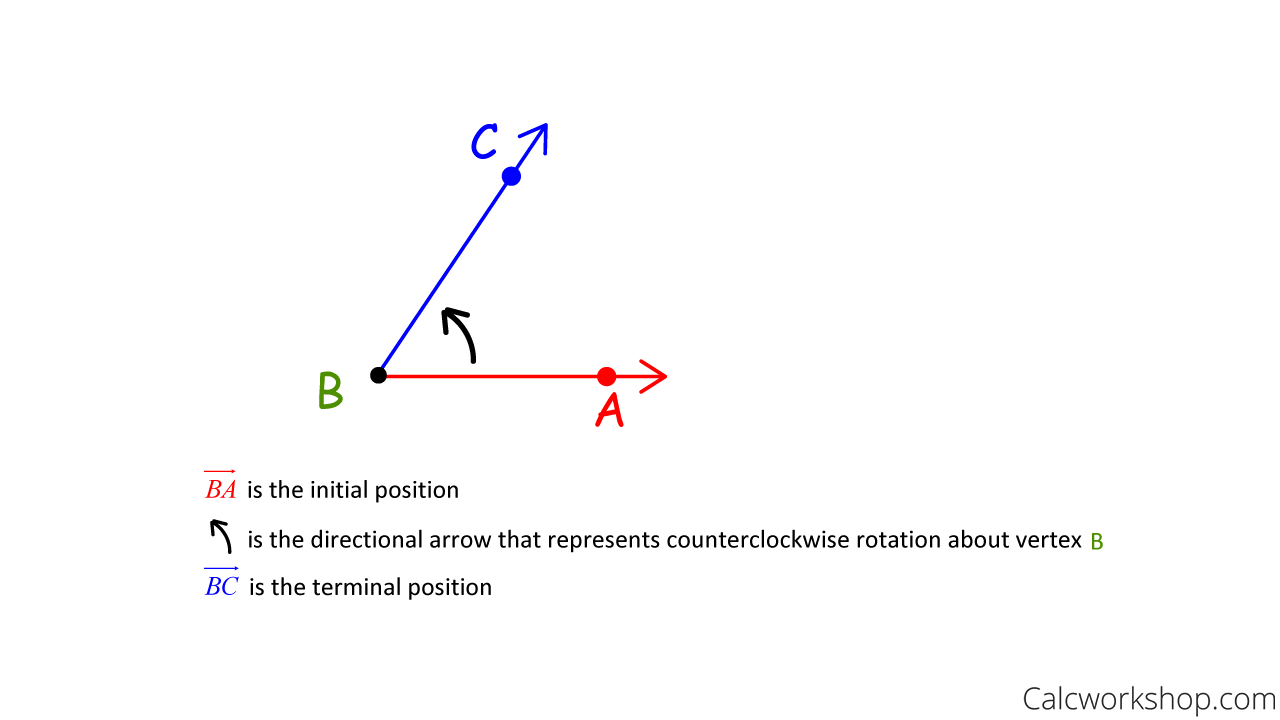
Angle Of Rotation Terminal And Initial Sides
Gifted with this new definition, we can see that angles are pretty powerful things!
Sketching An Angle In Standard Position
But how do we sketch an angle?
We begin with standard position.
First, we recall the coordinate plane where the four quadrants are formed by the intersection of the x and y axes at the origin.

Coordinate Plane Quadrants
Next, we place our initial side in standard position. All this means is that the vertex of the angle is located at the origin, and the initial side must coincide with the positive x-axis.
Initial Side – Standard Position
Lastly, we form the angle. This is found by the amount of rotation from the initial side on the positive x-axis to the terminal side.
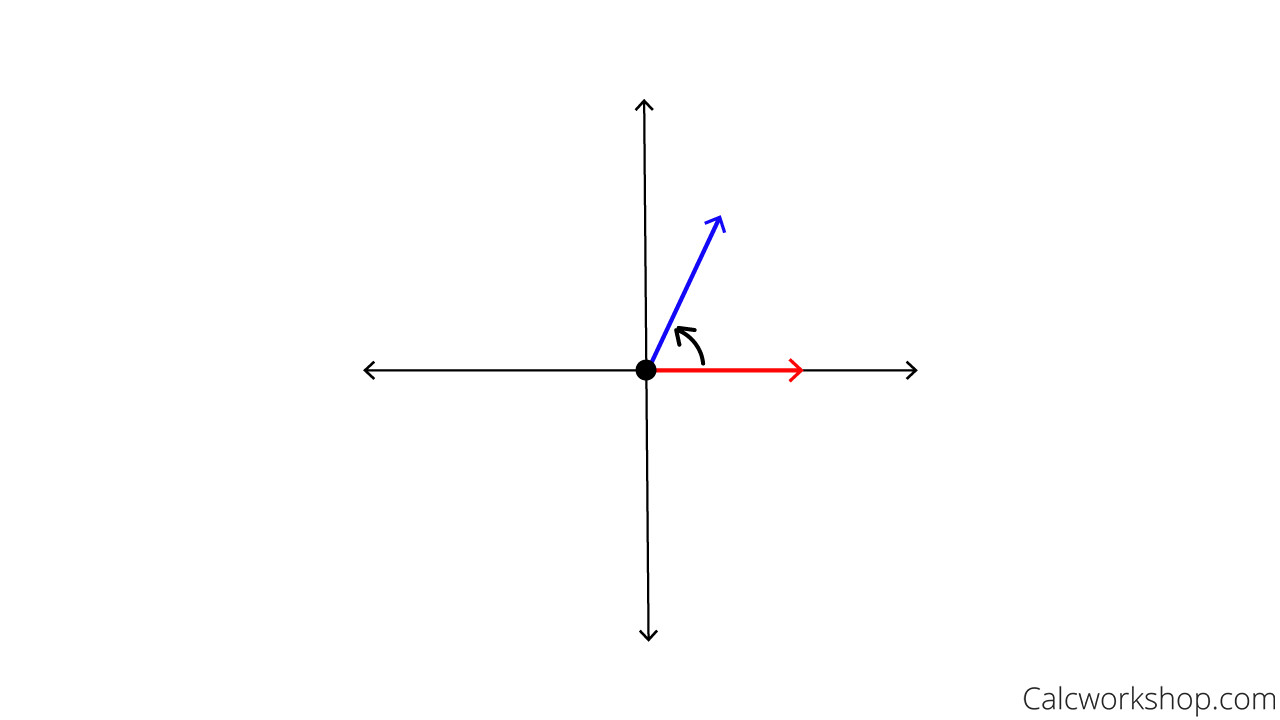
Counterclockwise Rotation Of The Terminal Side Makes Positive Angles
While this may seem strange at first, I promise you that it will make sense with a little practice.
Practice Problem
Let’s look at an example of sketching an angle of 210 degrees in standard position where we follow the three steps listed above.
- Draw the initial side on the positive x-axis.
- Determine which quadrant 210 degrees would fall.
- Sketch the terminal side in QIII and place the directional arrow.

Initial Side – Standard Position
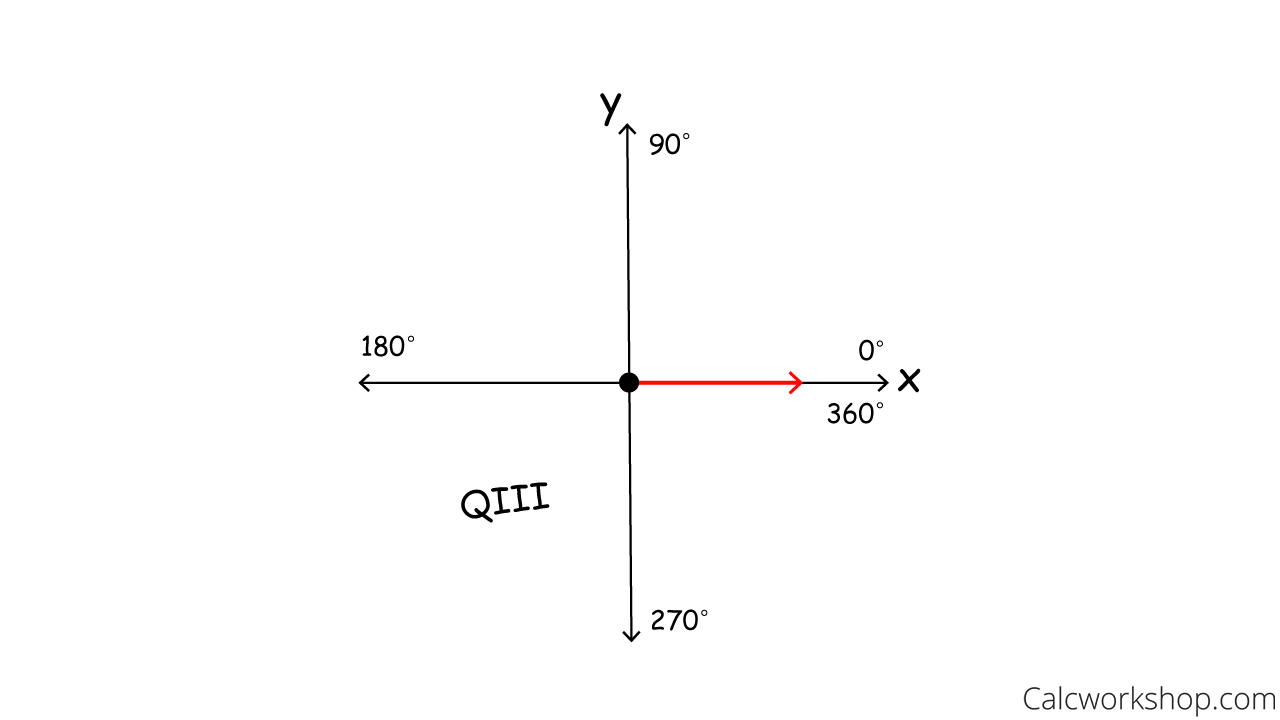
Label 0 90 180 270 360 Degrees
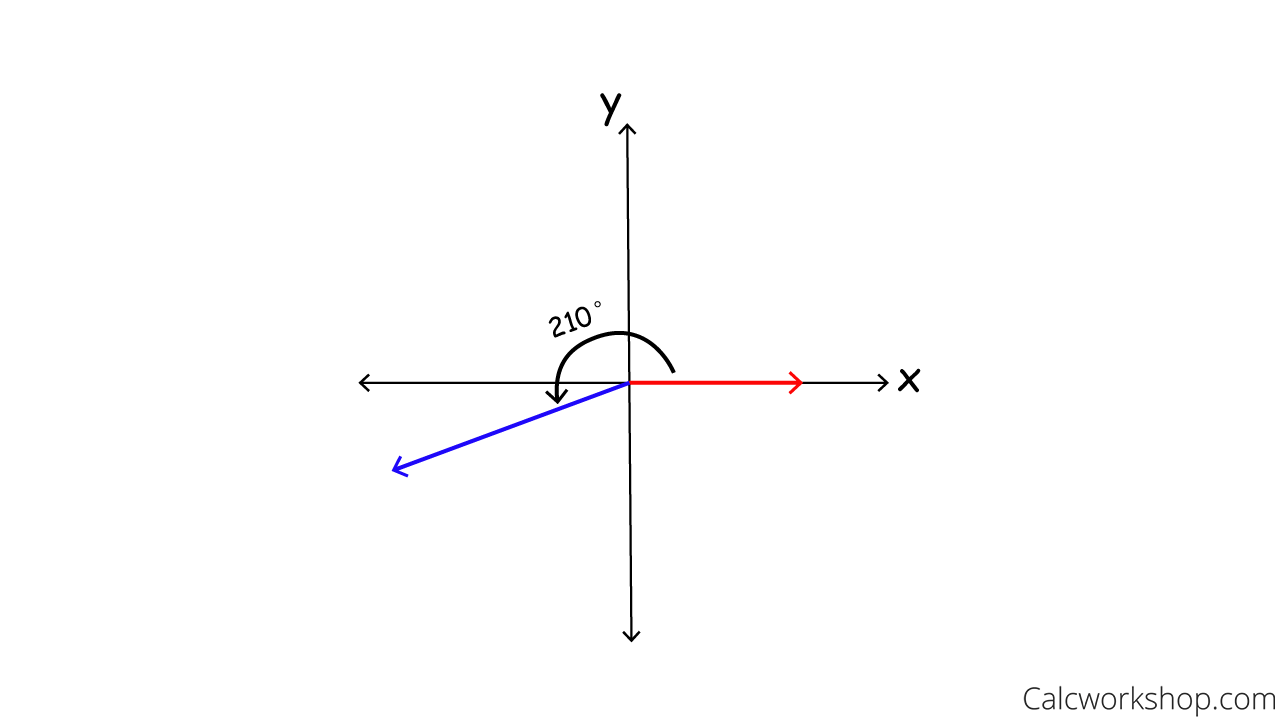
Sketch Angle 210 Degree Rotation
How To Find Coterminal Angles
So coterminal angles are two angles that have the same initial side and the same terminal side, but different amounts of rotation as noted by Emory University.
To help us understand this idea better, let’s look at the Latin root of this word.
“Co” is the Latin prefix that means two things join or come together and “terminal” means to end or conclude. Therefore, coterminal means two things end or conclude together at the same place!
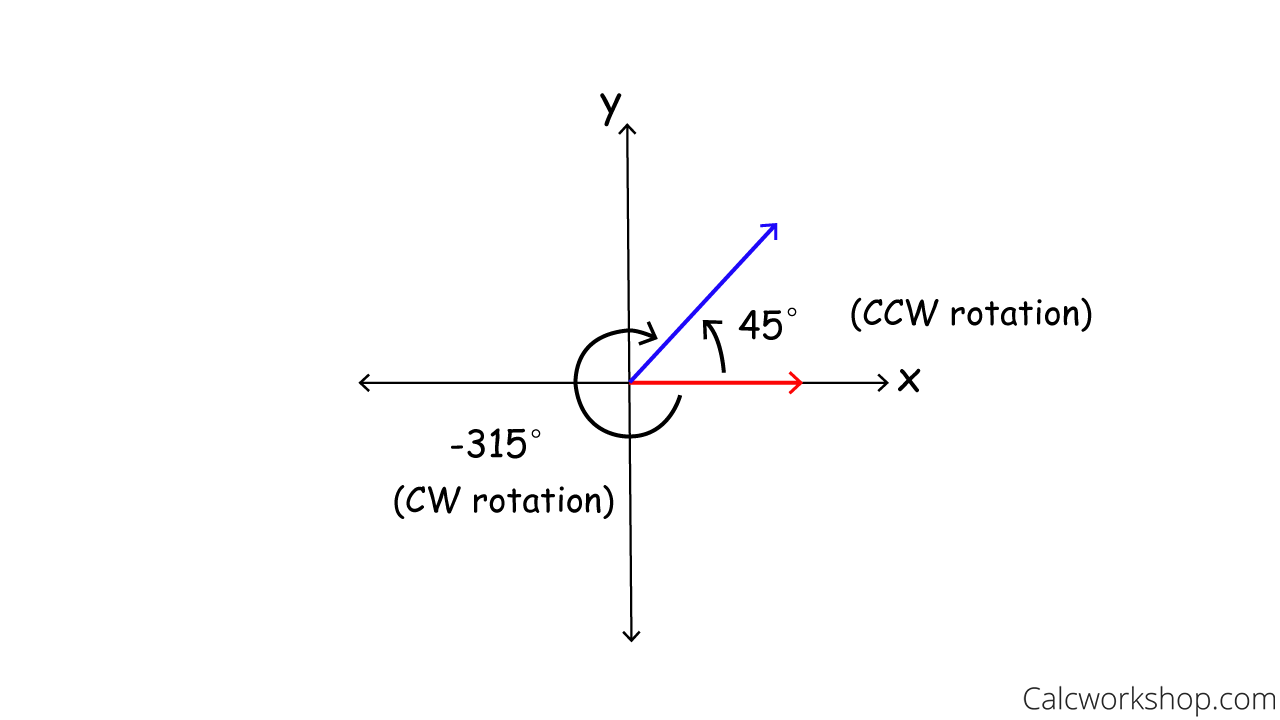
Negative Vs Positive Angle
What this ultimately means is that an angle can be both positive or negative, depending on which direction we rotate: counterclockwise (CCW) or clockwise (CW), and that an angle can be represented in more than one way.
Key Point: Since we know that one rotation around the circle is 360 degrees, finding coterminal angles is as easy as adding or subtracting multiples of 360 to each angle. This means that there is an infinite number of ways to represent the same angle and a variety of ways to measure each angle.
In this lesson, we will work with rotations and degrees.
Using The Formula
Okay, so to make sense of this, we can utilize the following formula, as it helps us to find infinite coterminal angles.
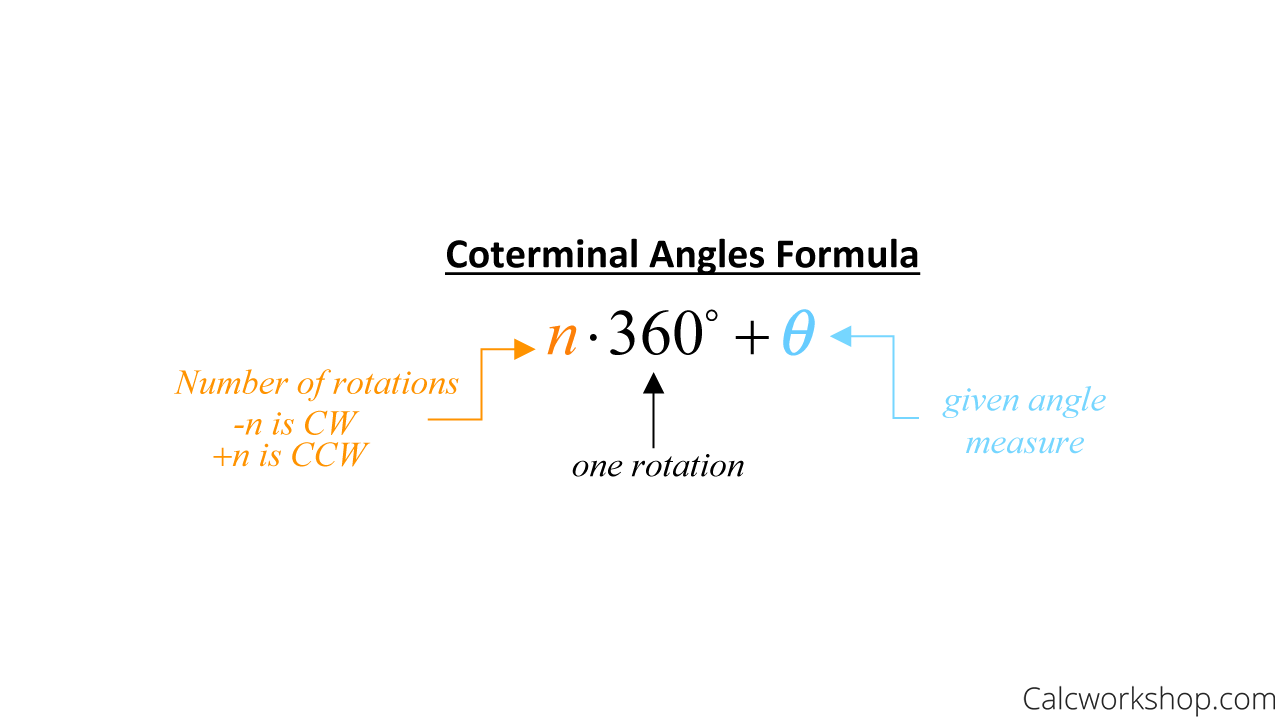
Coterminal Angle Formula
Cool!
A Few Basic Examples
Let’s see how we can put this formula to work by finding two coterminal angles, one positive and one negative, to 80 degrees.
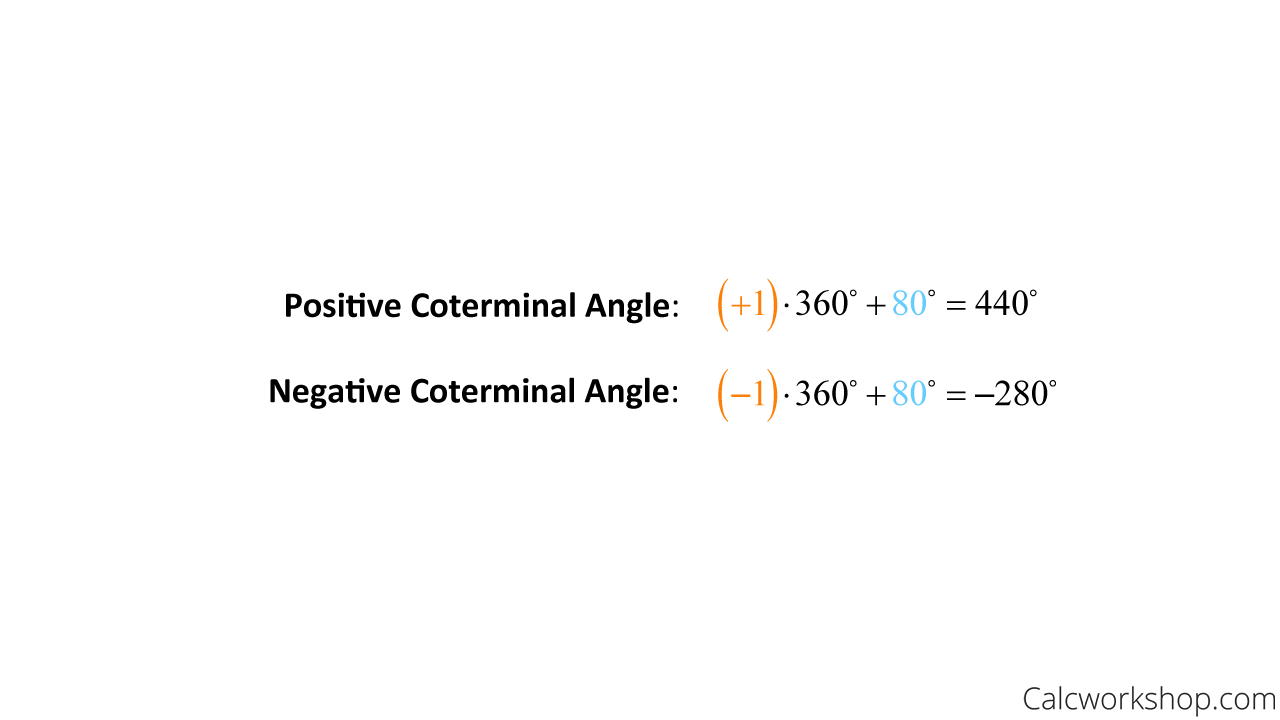
Find Positive And Negative Coterminal Angles — Example
Please note that 440 and -280 are just two of an infinite number of possibilities. All we have to do is change the value of “n” to find more coterminal measures!
Nice!
Some Harder Examples
But what if we are asked to find a coterminal angle less than 360 but greater than zero? Well, we will either need to add or subtract 360 from the given angle until our coterminal angle is between 0 and 360, as the following examples nicely illustrate.
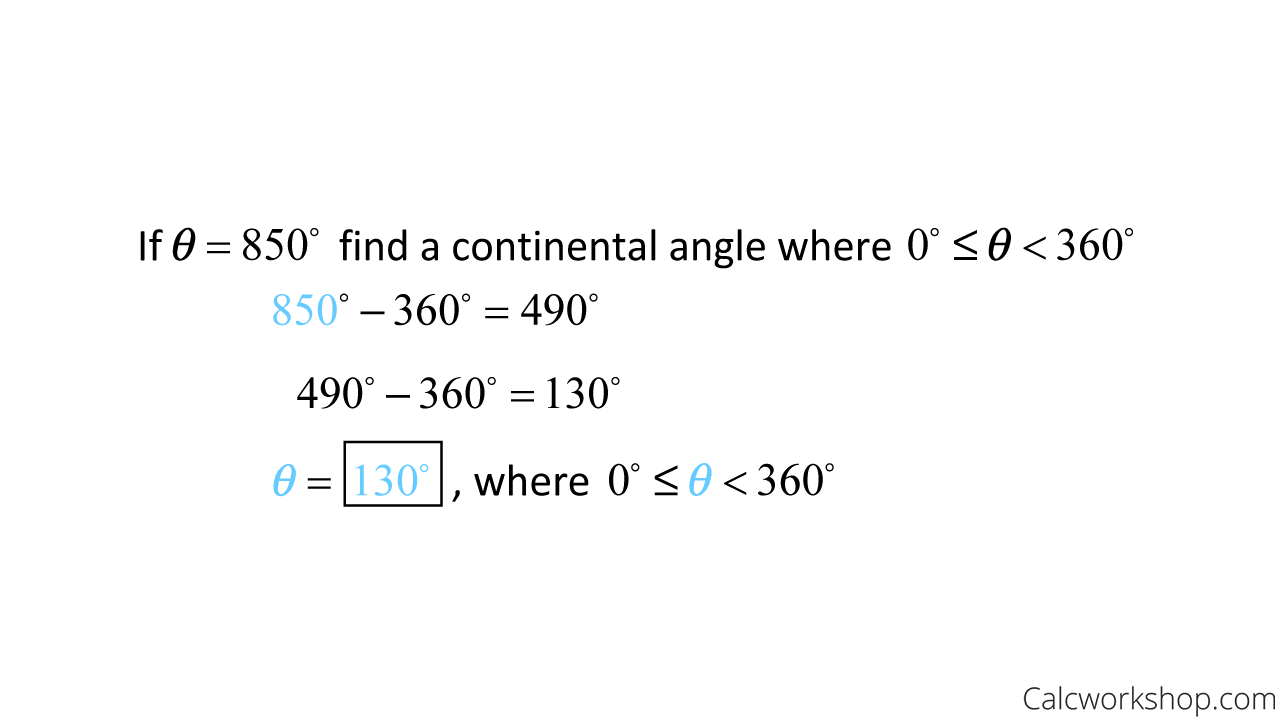
How To Find Coterminal Angles Between 0 And 360 Degrees
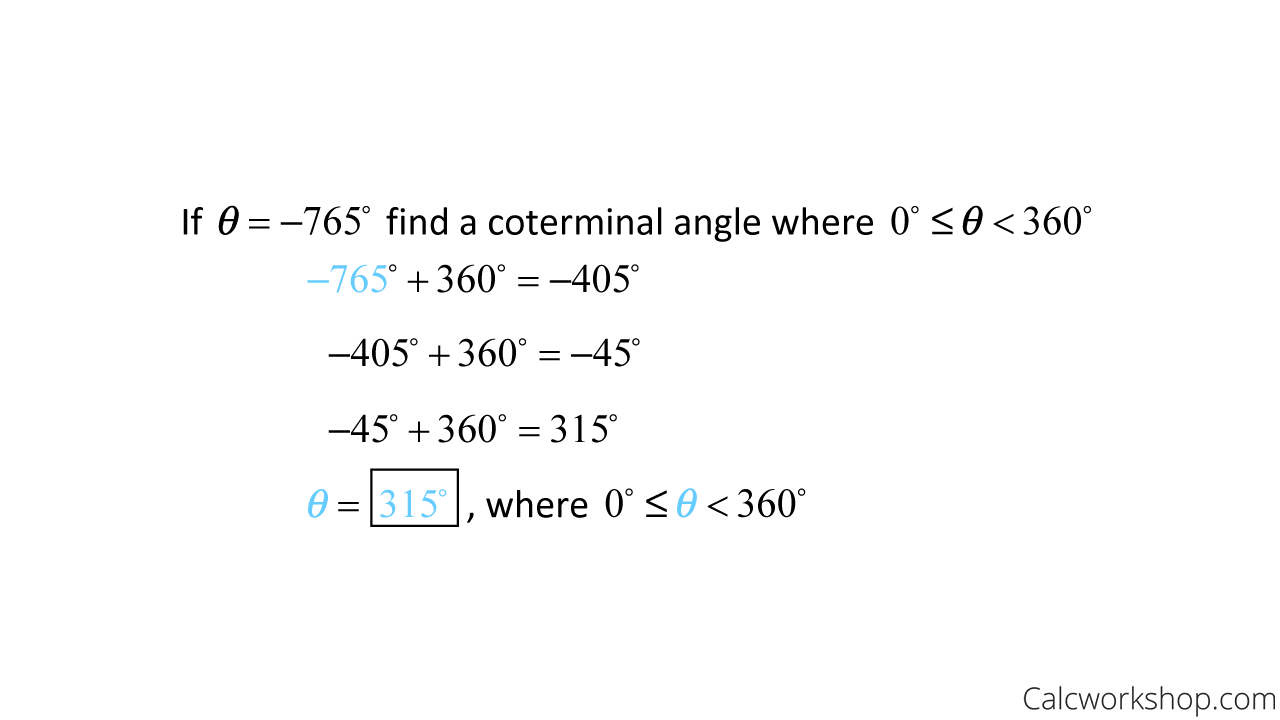
How To Find Coterminal Angles With Negative Degrees
Because 850 was bigger than 360, we subtracted, and because -765 was smaller than 0, we added.
So, that’s all there is to it!
Summary & Path Forward
Coterminal angles can be positive and negative and involve rotations of multiples of 360 degrees!
In fact, coterminal angles allow us to have infinite representations of angles in standard position with the same terminal side.
This video will explore angles in standard position using rotations and degrees and find coterminal angles using various examples.
Here we go!
Video Tutorial w/ Full Lesson & Detailed Examples
58 min
- Intro to Video: Coterminal Angles and Angles and the Coordinate Plane
- 00:00:39 Overview of Angles and Their Measure
- 00:05:42 Standard Position and Coterminal Angles
- 00:12:34 Plot each angle in standard position and determine degree measure (Examples #1-4)
- Exclusive Content for Members Only
- 00:20:43 Sketch each angle in standard position and determine which quadrant in which it lies (Examples #5-10)
- 00:28:47 Given an angle in standard position, find a coterminal angle and sketch (Examples #11-13)
- 00:38:43 Starting with an angle in standard position identify two coterminal angles (Examples #14-15)
- 00:45:21 Determine the quadrant(s) for each given angle (Examples #16-21)
- 00:51:30 Find a coterminal angle within a specified domain (Examples #22-25)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.