In our previous lesson we learned all about some really neat applications of right triangles: angle of elevation and depression.
Well, in this lesson we’re going to learn all about Navigation and Construction!
Now, in order to tackle questions that deal with Navigation and Construction we’re going to have to introduce some new words and definitions into our vocabulary:
- Course
- Bearing
- Pitch
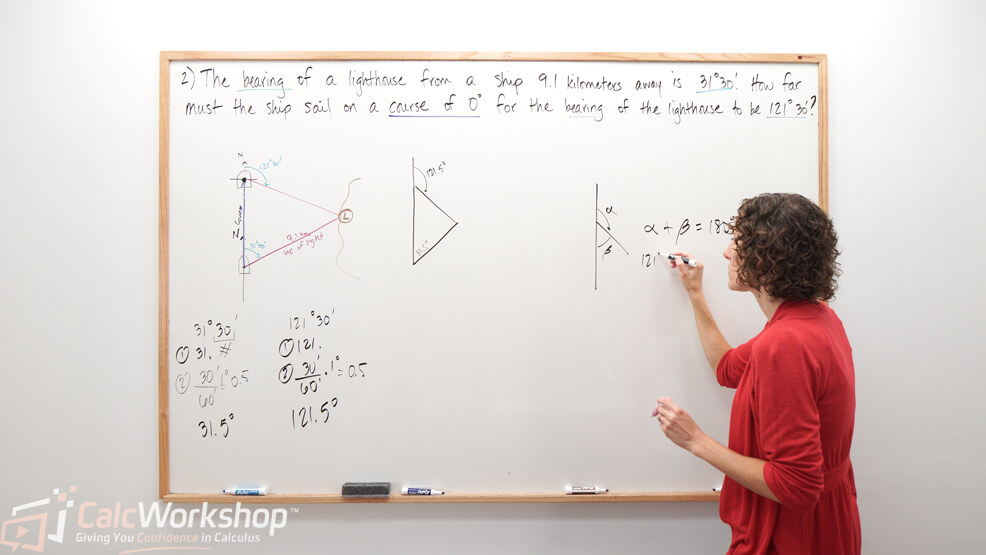
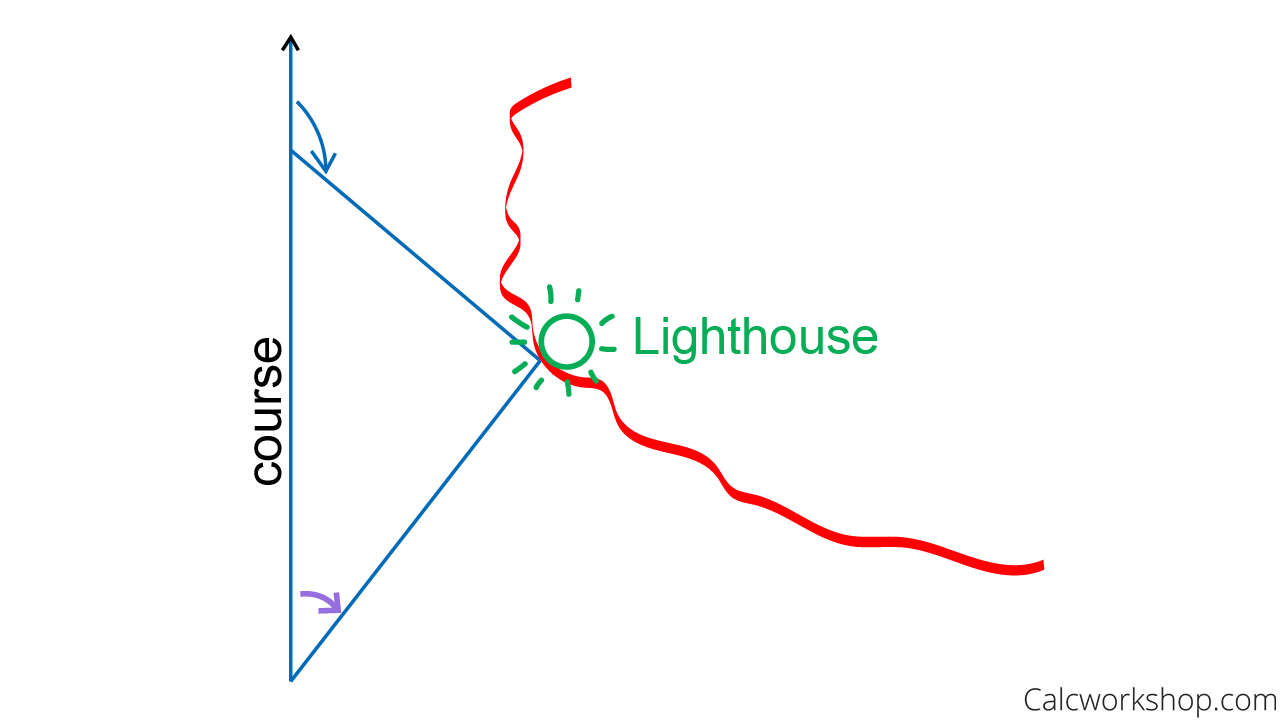
In navigation, the course of a ship or a plane or a person hiking through the woods, is the angle measured clockwise from north to the line of travel.
Huh? I still don’t get it.
Using Right Triangles to find Bearing and Course
Okay, so imagine that you are on a hike and you have a compass on your head. Your footsteps mark out the line of travel and the angle measured from north on the compass on your head measures the courses (the angle).
Ok, so now that I’ve got a better understanding of course, but what’s bearing?
I’ve always heard the phrases, “you have to set your course,” and “get your bearings.” Aren’t they same thing?
Formally, bearing of a line of sight is the angle measured clockwise from north to the line of sight.
What?
All this means is the a bearing is nothing more than the direction from one object to another, as nicely summarized by CK-12.
So imagine, once again, that as you are hiking/walking a specified course you spot a beautiful flower off in the distance. This angle, measured from that compass on top of your head to the flower is the bearing.
We’re going to walk through countless examples to illustrate both of these concepts in detail; once you see it in action, it will all become clear.
Alright, so what this idea of pitch? Are we talking about a baseball pitch?
Understanding Span and Pitch
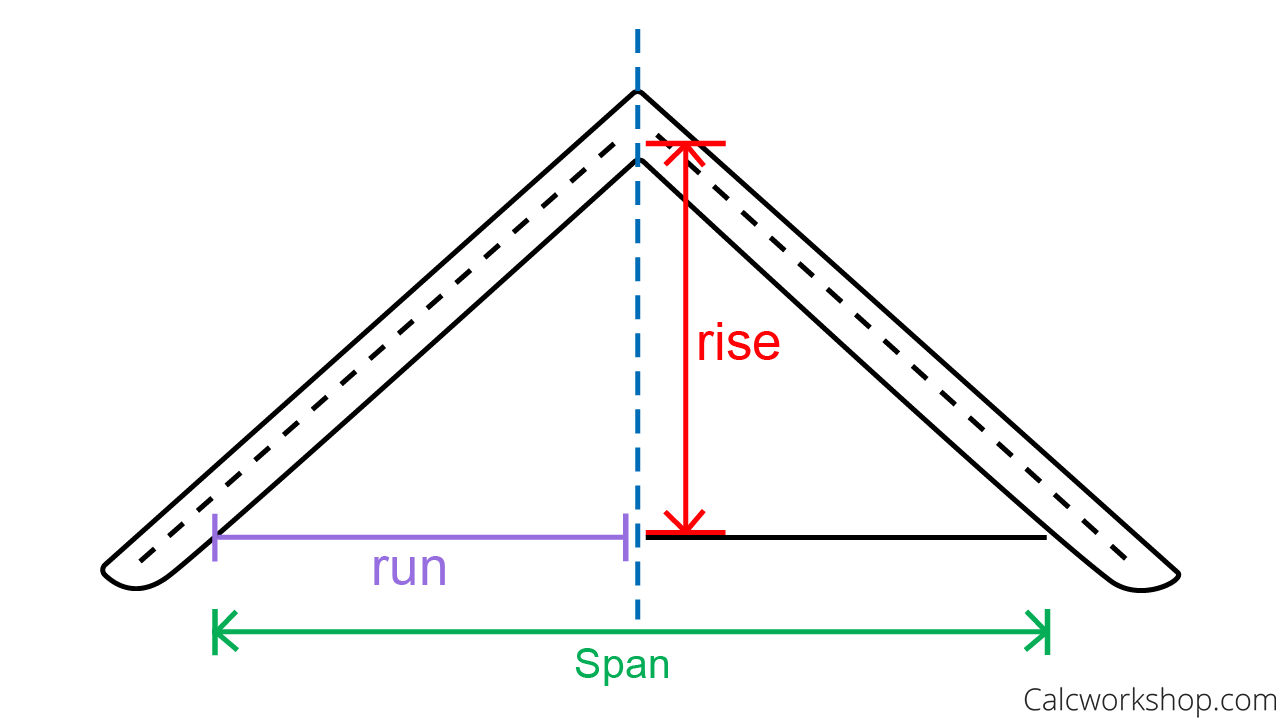
No, we’re not talking about throwing a pitch, but rather the term that architects and carpenters refer to as the ratio of the rise divided by the span of a roof.
We’re so used to the idea of slope, or the rate of change, which is found by looking at the rise over the run…ahh, those amazing right triangles again!
Well, we do something very similar when finding the pitch, but instead of just looking at the right triangle created by the rise and run, we in essence double the run to create the span.
Okay, picture a house with a symmetrical roof. All this means is that our roof looks like an isosceles triangle, where there is a base and the two legs are the same length. If we calculate the height of the triangle (rise) and the base of the triangle (span), then the ratio of these to values determines the pitch.
Don’t fear, if you can use the Pythagorean Theorem, then you can be an architect or carpenter and build a roof or stairs!
In fact, right triangles and trigonometry help us to not only find the angle of trusses that support a roof, but they ensure that the foundation of our house, or any other building, is level and stable.
The power of trigonometry is foundational to so many jobs, as nicely stated by the Houston Chronicle, and allows us to put our math skills into action.
Applications of Right Triangles – Video
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.