Did you know that a tree is a connected graph with no simple cycles?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
This means that an undirected graph is a tree if and only if there is a simple path between any two vertices.
And in graph theory, a graph with no cycles is called an acyclic graph. And a disjoint collection of acyclic trees is called a forest.
For example, the three graphs below are all trees, and together they create a forest of three components.

Graph Forest
Rooted Tree
Now a rooted tree is a tree in which one vertex has been designated as the root, and every edge is directly away from the root. I want you to think of a family tree where the oldest known relative is at the top of the tree, and all descendants are branched down from this one ancestor. This is the very idea of a rooted tree in graph theory.
Below is an example of a rooted tree and will help to highlight some of the critical vocabularies such as ancestors, descendants, parents, children, siblings, internal vertices, and leaves.
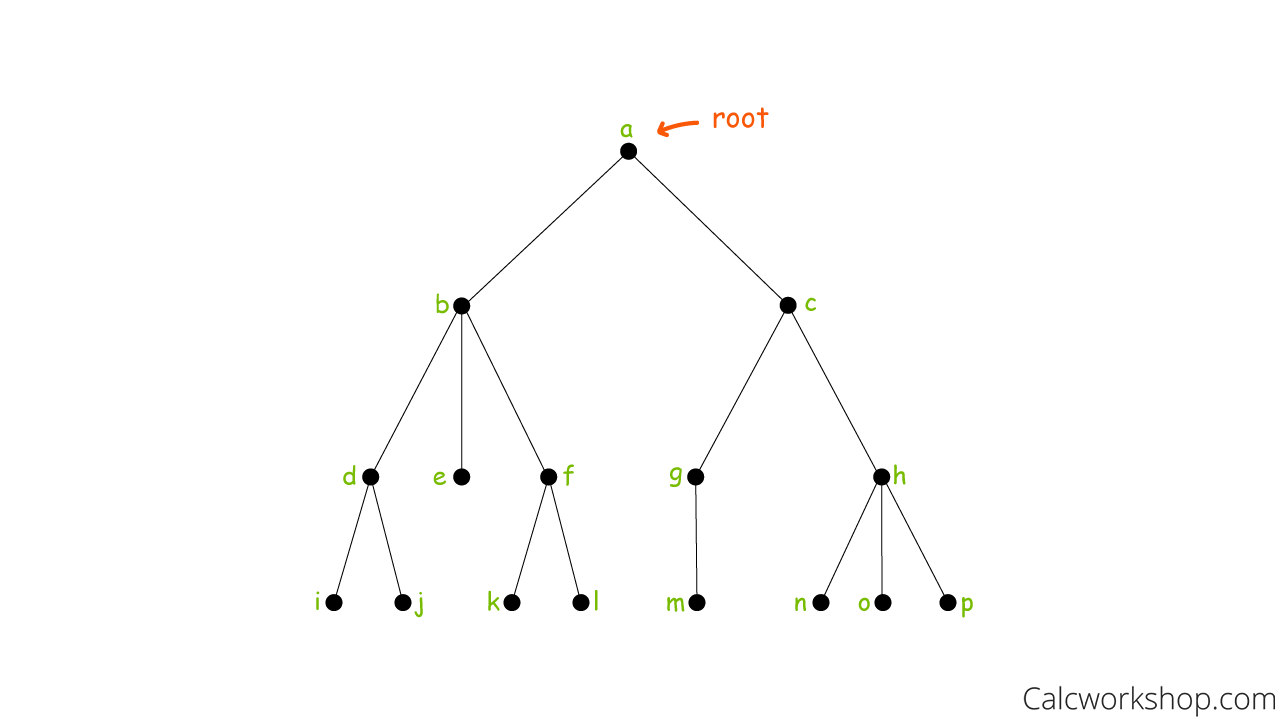
Rooted Tree Graph
- Children of a: b and c
- Parent of b and c: a
- Children of b: d, e and f (d, e and f are siblings)
- Children of c: g and h (g and h are siblings)
- Parent of d, e, and f: b
- Parent of g and h: c
- Leaves: e, i, j, k, l, m, n, o, p (vertices that do not have children)
- Ancestors of m: g, c, and an (all vertices in the path from the root to the desired vertex)
- Descendants of c: g, h, m, n, o, p (all vertices originating from the indicated vertex)
- Internal vertices: b, c, d, f, g, h (vertices that have children)
The University of Hawaii has some additional examples.
Subtree
And a subtree is a subgraph of a tree consisting of the indicated vertex and all of its descendants. For example, using our rooted tree from above, the subtree of h would be
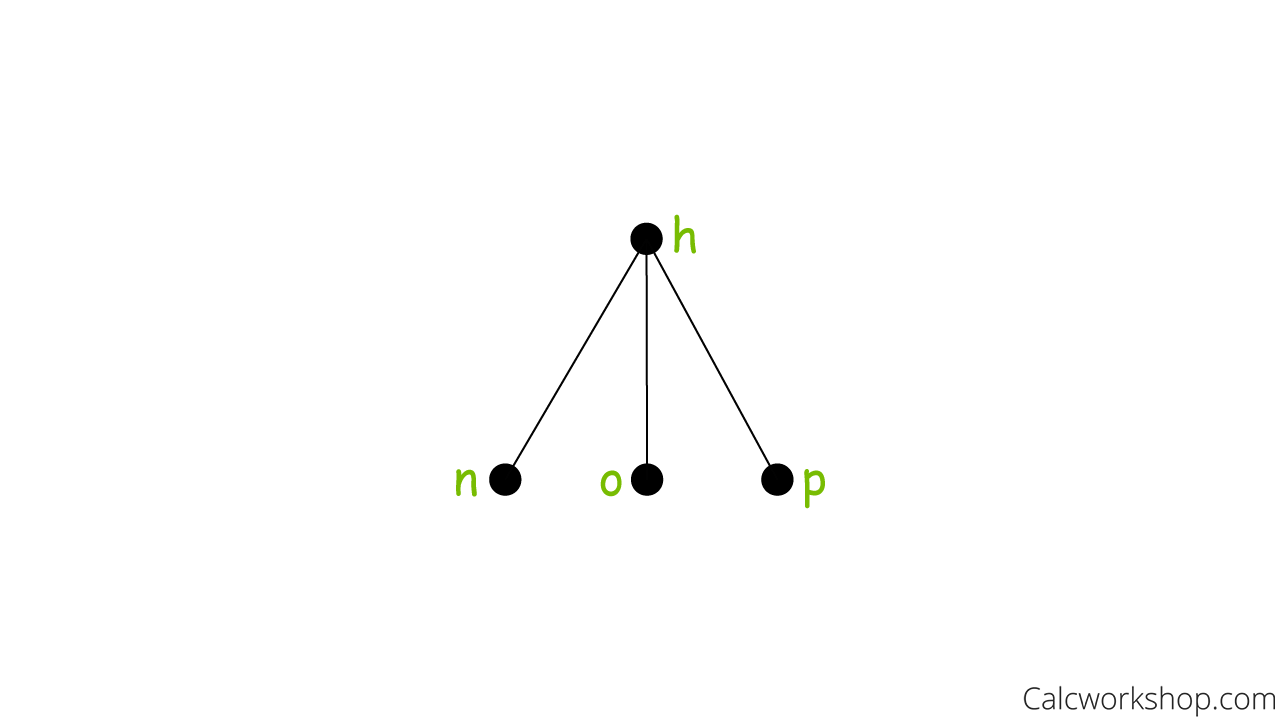
Subtree Example
M-ary Tree
Additionally, a rooted tree is called an m-ary tree if every internal node has no more than m children. And a full m-ary tree occurs when every internal node has precisely m children. An m-ary tree with m=2 is called a binary tree. Below is an example of some m-ary trees.

M-Ary Binary Tree — Examples
Levels
Furthermore, a tree’s vertices are organized into levels, based on how many edges or branches away from the root they are. The root is defined to be level 0, and its children are level 1, their children are level 2, and so forth. And the height of a tree is the maximum number of levels from root to leaf.
For example, let’s determine the level and height for the following trees.
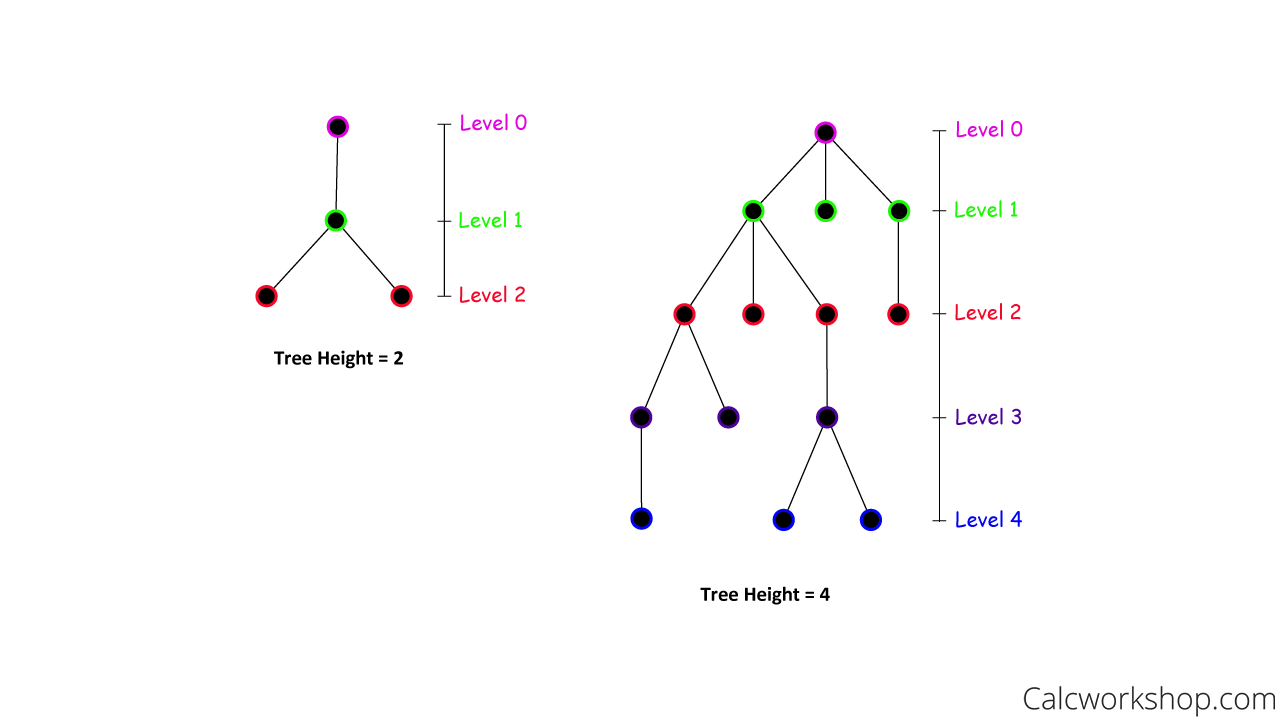
Tree Height Level — Example
Theorems
Moreover, some essential theorems and properties help us determine the number of edges, vertices, leaves, level, and height.

Tree Theorem — Edges Vertices Leaves Height
Let’s work on a few problems using our theorems above to help make sense of things.
Example – Vertices
How many vertices does a full 8-ary tree with 121 internal vertices have?

Determine Number Vertices — Example
Example – Leaves
Assume there is a 3-ary tree with 103 vertices. How many leaves does it have?

Number Leaves — Example
Example – Internal Vertices
How many internal vertices does a full 5-ary tree with 101 leaves have?

Number Internal Vertices — Example
Example – Edges
Determine the number of edges a full 5-ary tree with 121 leaves have?
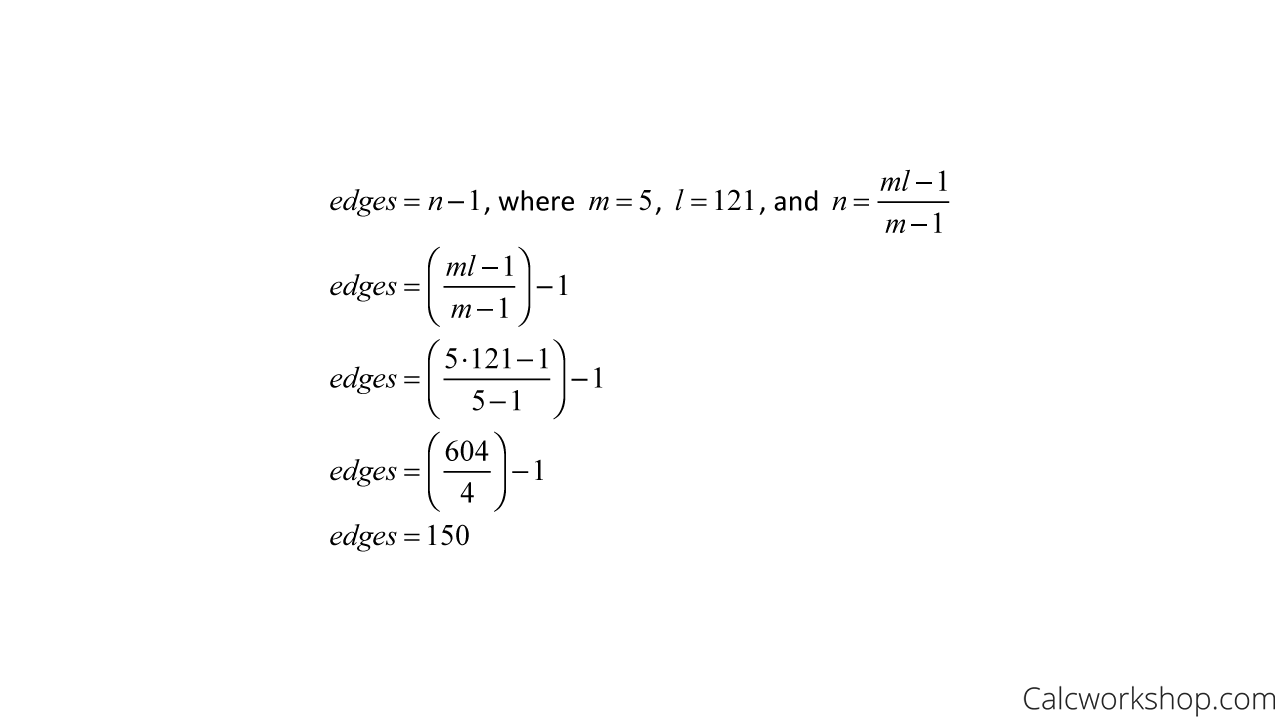
Number Of Edges In A Tree
See, using these theorems and formulas for trees isn’t so bad!
By working through countless examples, we will learn the basic properties of trees, see the importance that trees have in hierarchical structures, and use formulas to find the number of edges, leaves, and vertices for various m-ary trees.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.