Spanning Tree (Explained w/ 9 Step-by-Step Examples!)

Did you know that a spanning tree of an undirected graph is just a connected subgraph covering all the vertices with the minimum possible edges?

Jenn (B.S., M.Ed.) of Calcworkshop® teaching spanning trees

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

In fact, a graph may have more than one spanning tree, as a rule for producing a spanning tree with n vertices and m edges is to remove (m – n + 1 ) edges.

For example, suppose we are given the following undirected graph containing three edges and three vertices. How do we find its spanning trees?

Well, we simply start by removing one edge and see if the resulting graph is a tree.

And what we quickly notice, is that there are three possible spanning trees that we can generate from our undirected graph, depending on which edge we choose to remove.

Create Spanning Tree

Now, depending on the number of edges and vertices contained in closed, undirected graph will determine the number of edges that will need to be removed to produce a spanning tree. In fact, did you know that the maximum number of spanning trees for an undirected graph is

Max Number Spanning Tree Formula

This means we can take an undirected graph with a finite set of vertices and create a tree!

Okay, but what if we want to make a minimum spanning tree, where the weight is the smallest possible spanning tree?

Recall that the weight of an edge corresponds to its length or cost, and therefore the weight of a spanning tree is the sum of all the weights of its edges. Consequently, if we are asked to find a minimum spanning tree, or MST, we want to find the smallest sum of weights or lengths of the tree’s edges.

There are two primary algorithms for finding the minimum spanning tree:

Prim’s Algorithm.
Kruskal’s Algorithm.

Prim Algorithm

Prim’s algorithm finds the minimum spanning tree by starting with one node and then keeps adding new nodes from its nearest neighbor of minimum weight until the number of edges is one less than the number of vertices, as noted by Simon Fraser University.

Prim Algorithm Steps

Using the following undirected graph, let’s apply Prim’s algorithm to find the minimum spanning tree by starting at vertex “a”

Undirected Graph Use Prim Algorithm

Now we need to choose an adjacent path of minimum weight. Because both adjacent paths are of the same value of 5, we get to choose one, so let’s choose {af}.

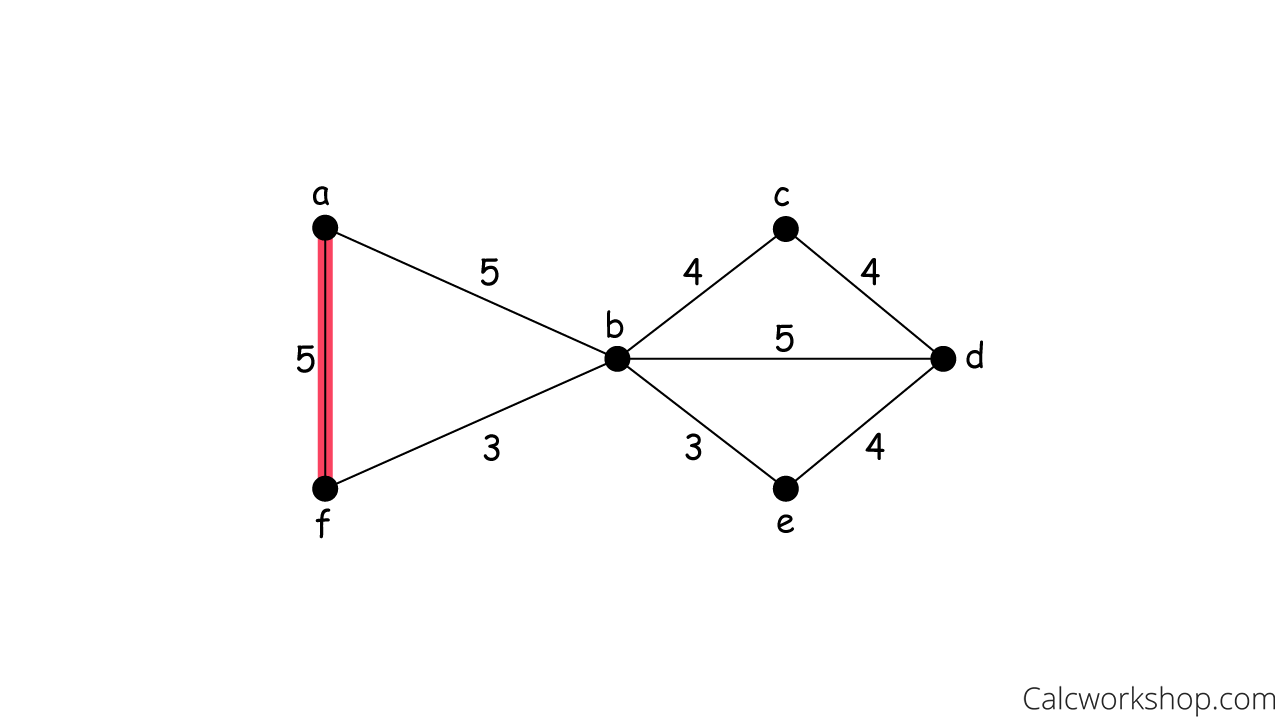
Prim Algorithm Choose Node

Now we select another adjacent edge of minimum weight, and so we select path {fb} because it has a minimum weight of 3.

Select Adjacent Edge 1

Next, we notice that we have three choices for our next adjacent path, either {bc} or {bd} or {be}. Because be is the path of minimum weight we choose this edge next.

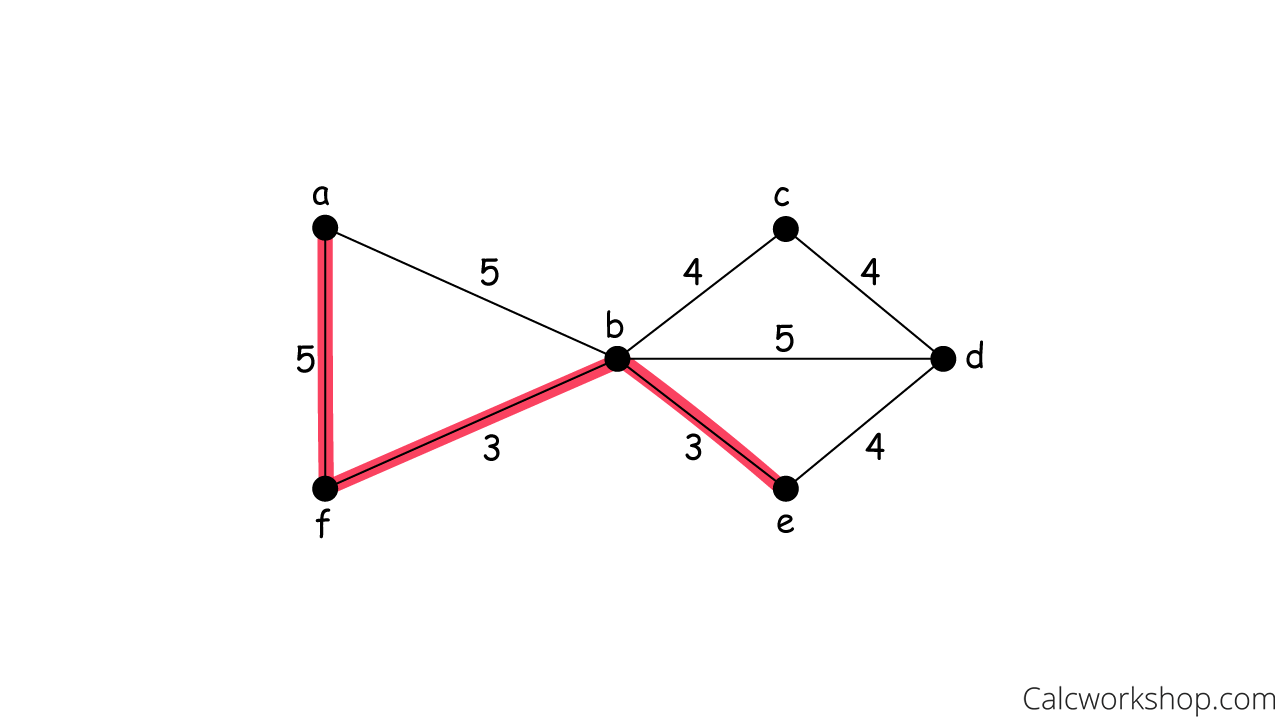
Select Adjacent Edge 2

Now we take a step back and must choose our next edge, because we are left with three edges of weight 4 and one of weight 5, we select those of minimum weight and choose path {bc}.

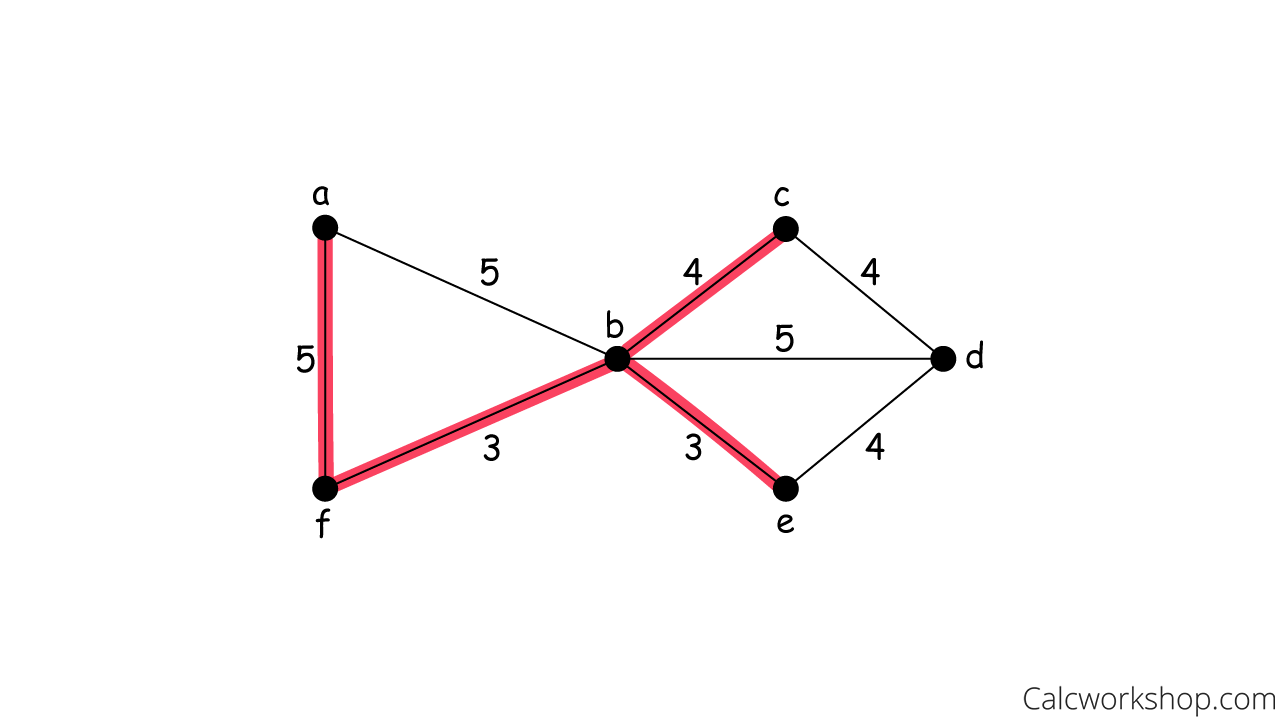
Selected Adjacent Edge 3

Finally, we must select either {cd} or {ed} …it doesn’t matter as they are both of same weight.

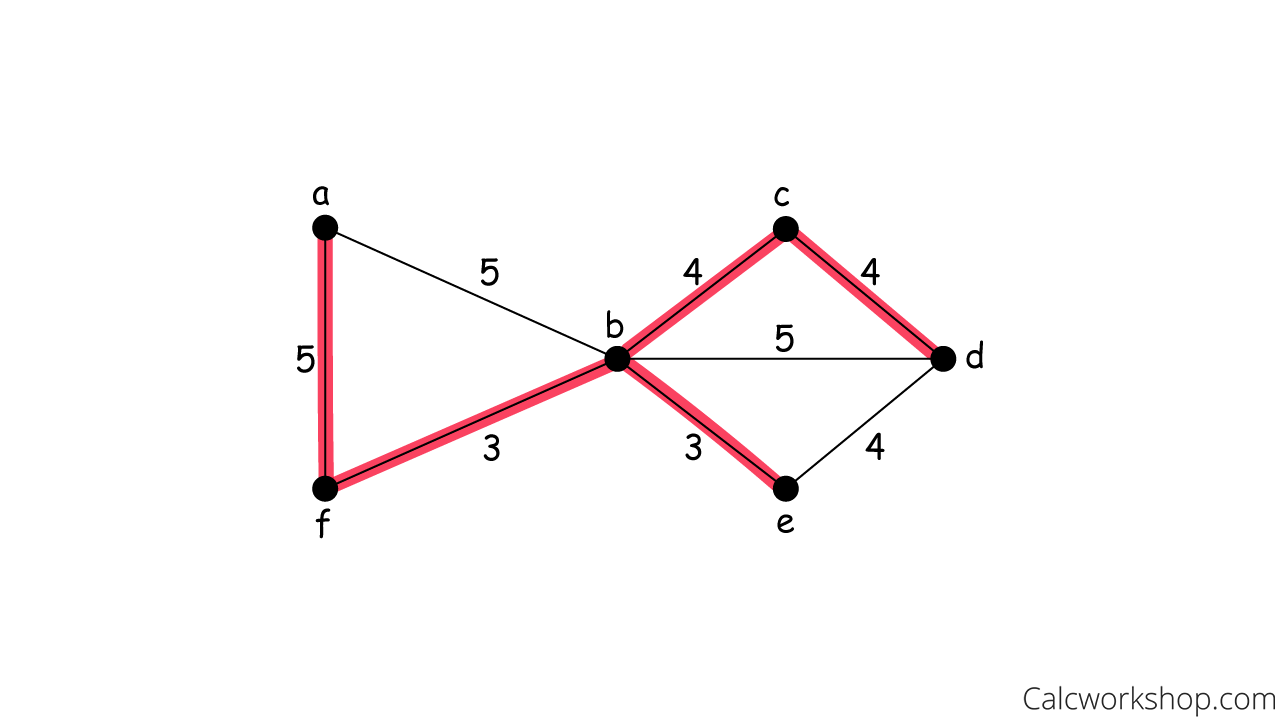
Prim Algorithm Example

So, in summary, Prim’s algorithm starts with a single node and grows a spanning tree by adding edges until every vertex is selected and the minimum spanning tree is built with a Minimal Total Cost = 5 + 3 + 3 + 4 + 4 = 19.

Kruskal Algorithm

Now let’s look at Kruskal’s algorithm and see how it differs in finding the MST.

Kruskal Algorithm Steps

Using the same undirected graph as above, let’s use Kruskal’s algorithm to find the minimum spanning tree by starting with the edge of least weight.

Undirected Graph Kruskal Algorithm

Notice that there were two edges of weight 3, so we choose one of them.

Min Weight Kruskal 1

Now, we select the other so that both edges of weight 3 are chosen.

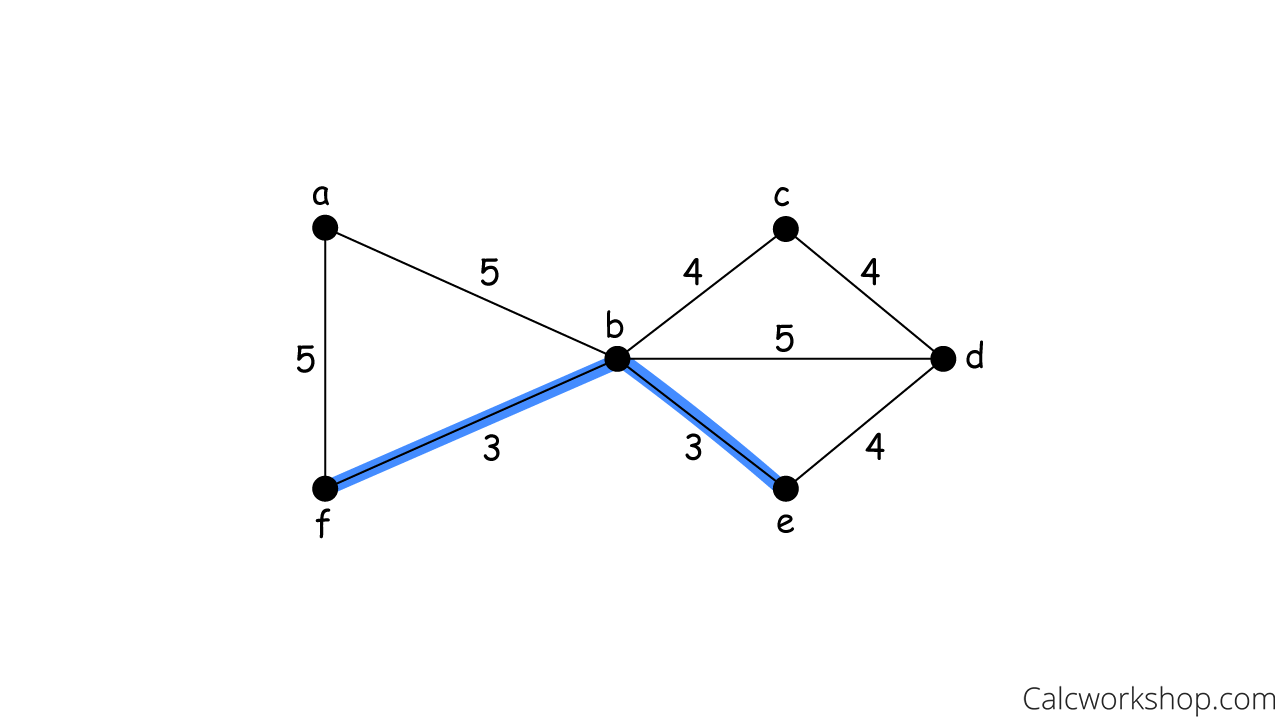
Min Weight Kruskal 2

Now we select an edge of next minimum cost, which is the value of 4.

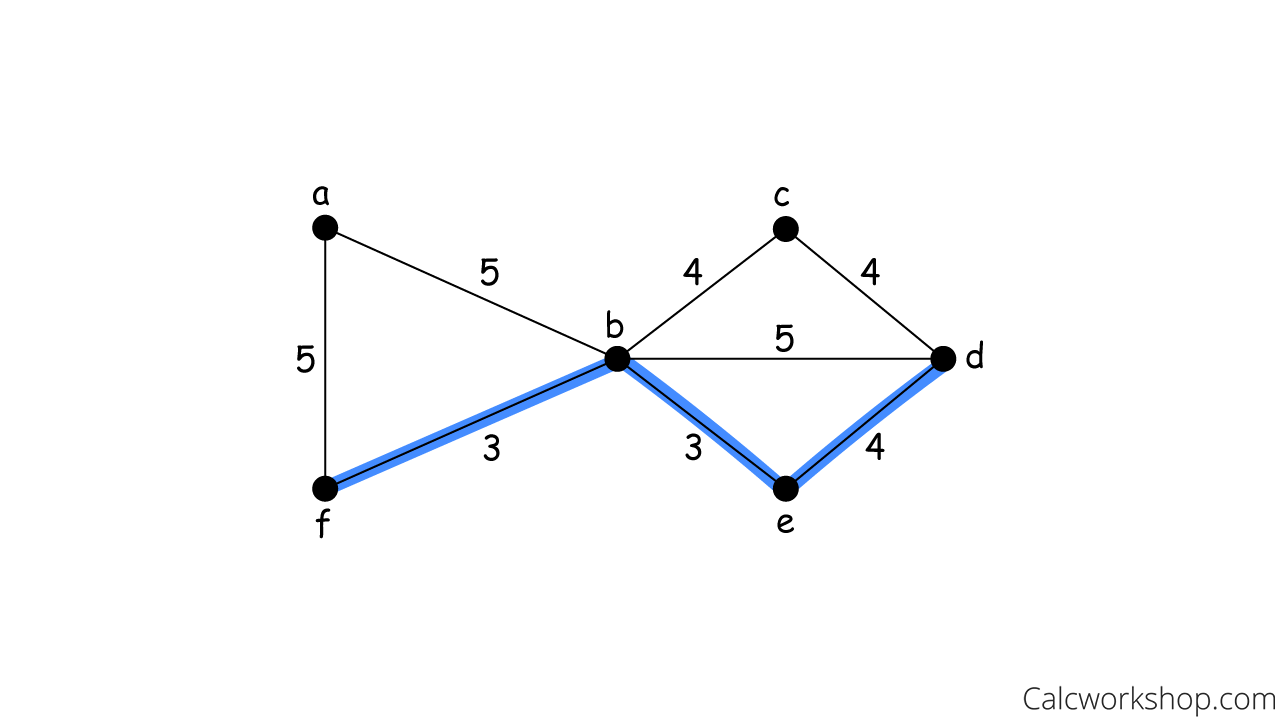
Min Weight Kruskal 3

Because there are three edges of cost 4, we simply choose one at at time, making sure that we don’t create a cycle.

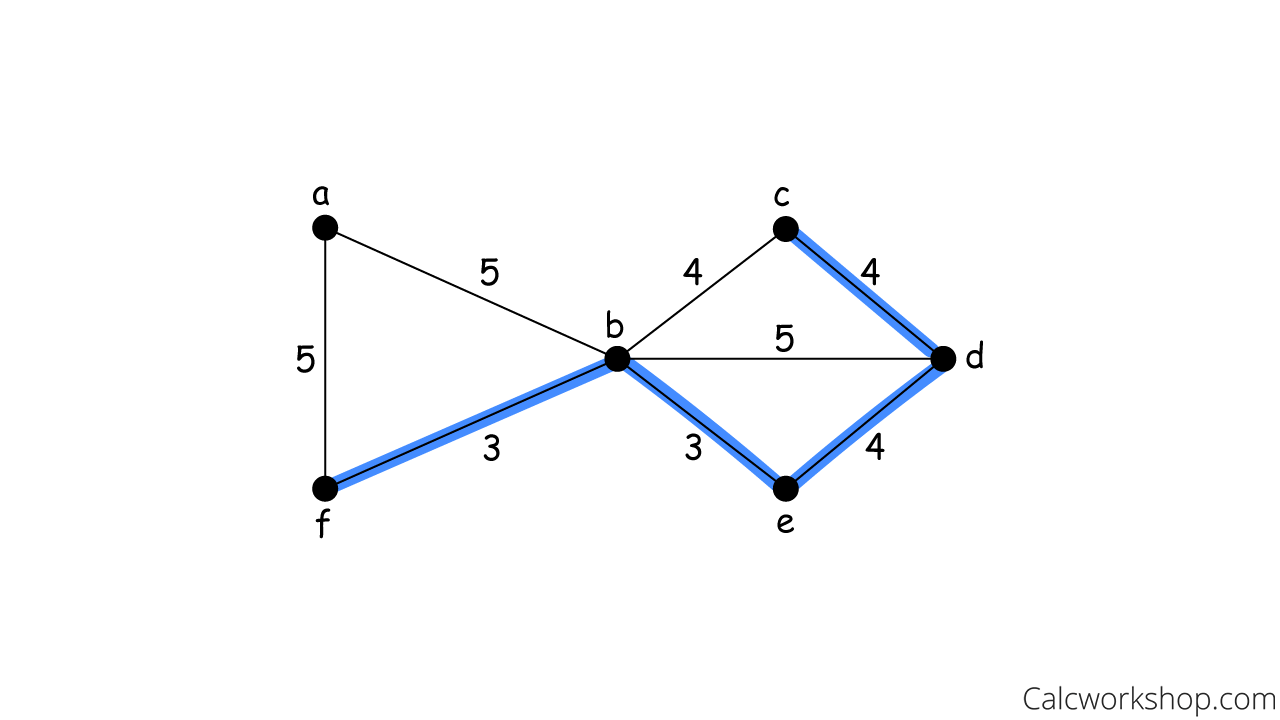
Min Weight Kruskal 4

Notice that while path {bc} has a cost 4, we can’t pick this path because it will create a cycle. Therefore we must choose an edge of cost 5 that will connect our tree and ensure that ever vertex is selected.

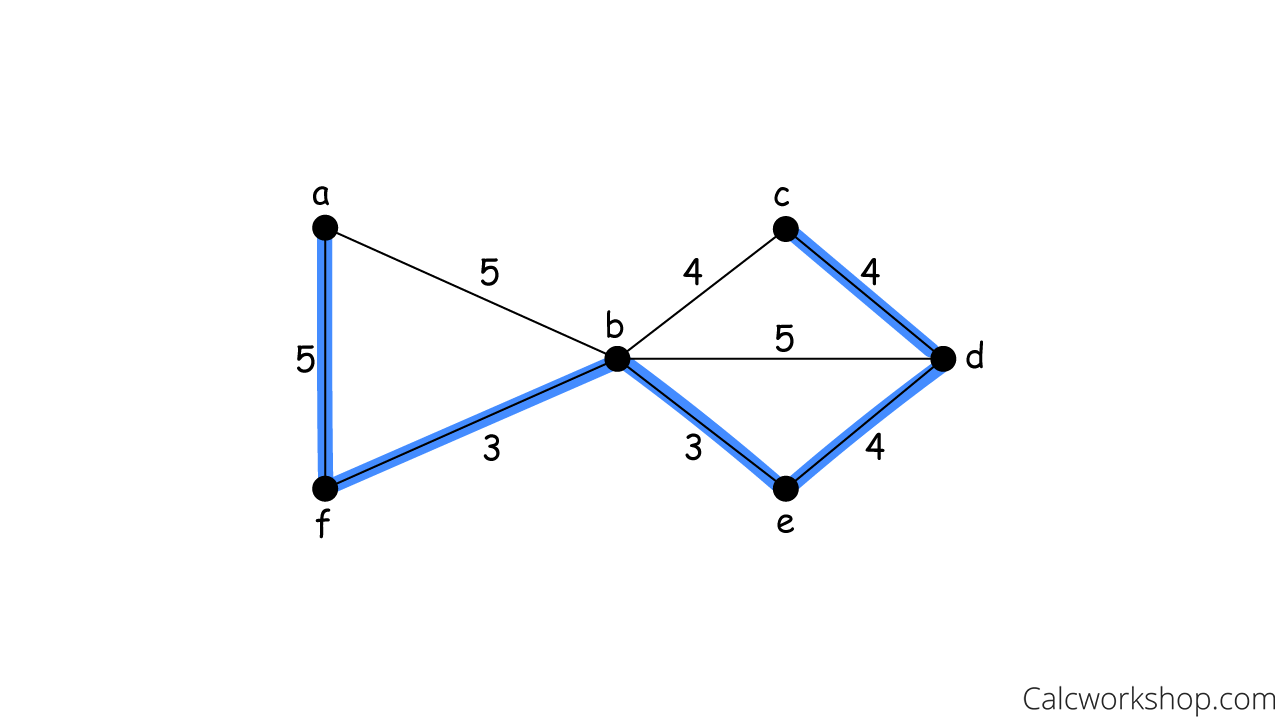
Kruskal Algorithm Example

So, Kruskal’s algorithm keeps adding edges of minimum weight until a minimum spanning tree is created — thus, giving us a Minimal Total Cost of 3 + 3 + 4 + 4 + 5 = 19

It is important to note that while Prim’s algorithm and Kruskal’s algorithm might produce different spanning trees, but they will always provide the same minimal cost. That means you can choose the algorithm you like the best to find the minimum spanning tree!

And lastly, we want to note that Prim’s Algorithm and Kruskal’s Algorithm are greedy algorithms, as they will always produce optimal results. A greedy algorithm generates a solution one piece at a time and offers the optimal result based on the available data. Simply put, a greedy algorithm makes the “best” choice in the current moment. Note that while it’s fast and effective for making decisions on a local level, it’s not always a good fit for global situations.

Video Tutorial w/ Full Lesson & Detailed Examples (Video)

$calcworkshop jenn teaching discrete math$

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.