What is an isomorphic graph?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
That’s exactly what you’re going to learn about in today’s discrete math lesson.
Let’s jump right in!
Two graphs are said to be equal if they have the exact same distinct elements, but sometimes two graphs can “appear equal” even if they aren’t, and that is the idea behind isomorphisms.
How To Tell If A Graph Is Isomorphic
If we are given two simple graphs, G and H. Graphs G and H are isomorphic if there is a structure that preserves a one-to-one correspondence between the vertices and edges.
In other words, the two graphs differ only by the names of the edges and vertices but are structurally equivalent as noted by Columbia University.
Method One – Checklist
Look at the two graphs below. Are they isomorphic?
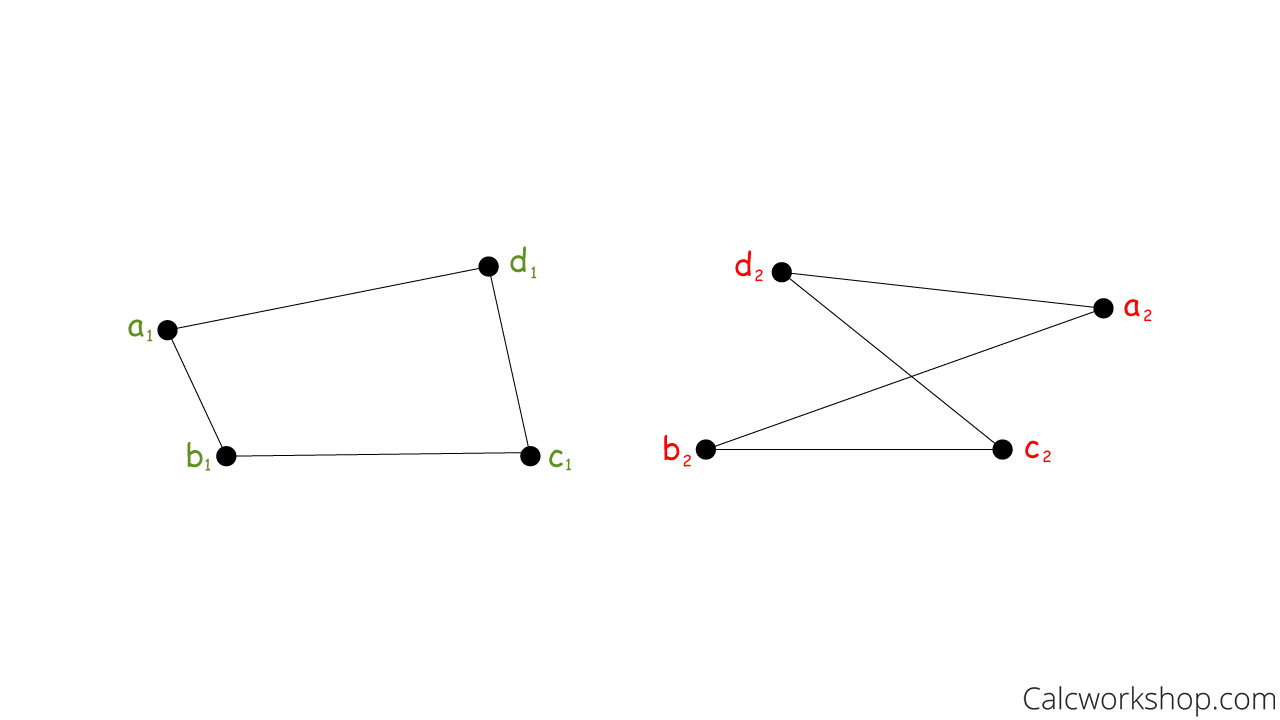
How To Tell If Two Graphs Are Isomorphic
All we have to do is ask the following questions:
- Are the number of vertices in both graphs the same? Yes, both graphs have 4 vertices.
- Are the number of edges in both graphs the same? Yes, both graphs have 4 edges.
- Is the degree sequence in both graphs the same? Yes, each vertex is of degree 2.
- If the vertices in one graph can form a cycle of length k, can we find the same cycle length in the other graph? Yes, each graph has a cycle of length 4.
And if we can answer yes to all four of the above questions, then the graphs are isomorphic. In other words, they are the equivalent graphs just in different forms.
Simply put,

Isomorphism Definition
Method Two – Relabeling
In addition to counting vertices, edges, degrees, and cycles, there is another easy way to verify an isomorphism between two simple graphs: relabeling.
Suppose we want to show the following two graphs are isomorphic.

Two Graphs — Isomorphic Examples
First, we check vertices and degrees and confirm that both graphs have 5 vertices and the degree sequence in ascending order is (2,2,2,3,3).
Now we methodically start labeling vertices by beginning with the vertices of degree 3 and marking a and b.
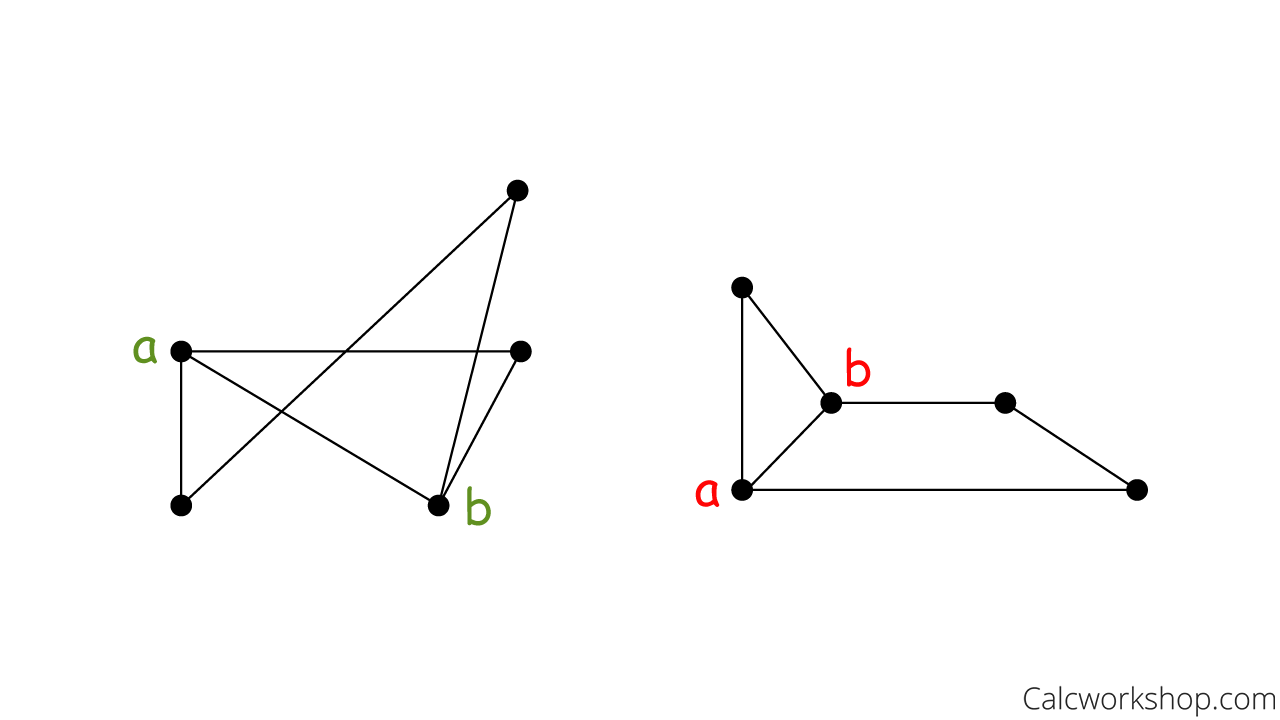
Label Odd Vertices
Next, we notice that in both graphs, there is a vertex that is adjacent to both a and b, so we label this vertex c in both graphs.
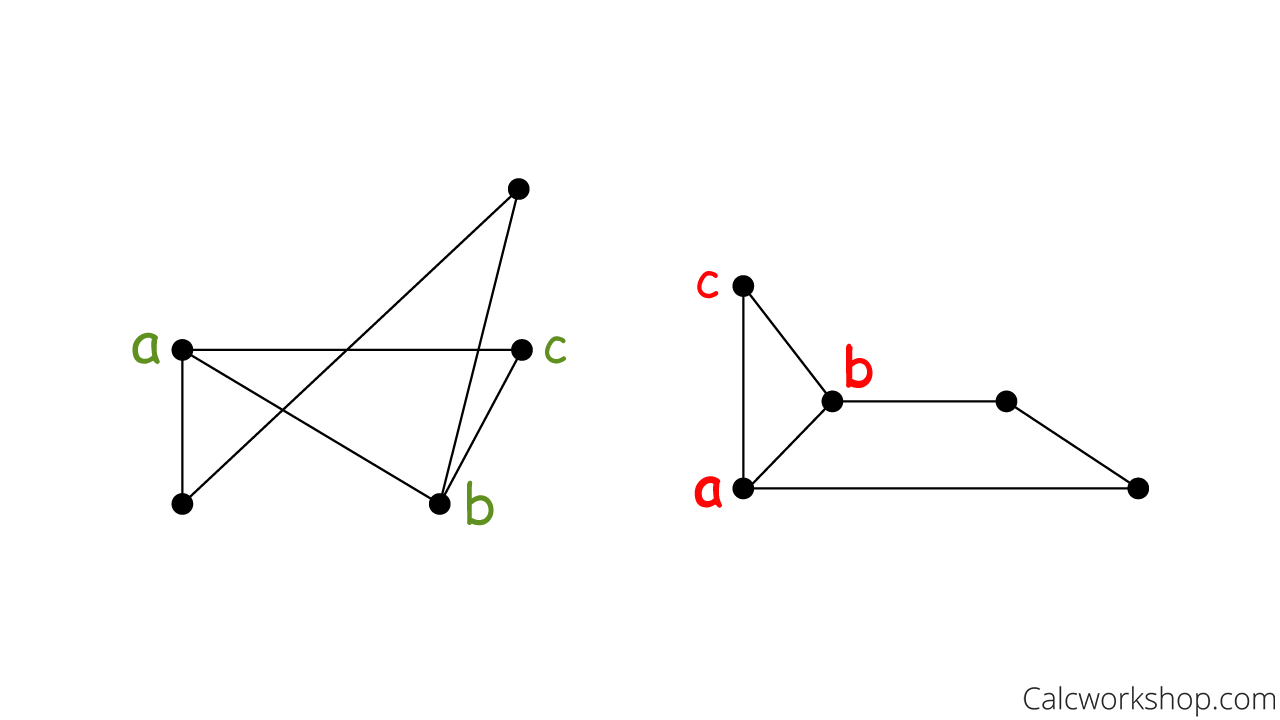
Label Adjacent Vertex
This now follows that there are two vertices left, and we label them according to d and e, where d is adjacent to a and e is adjacent to b.
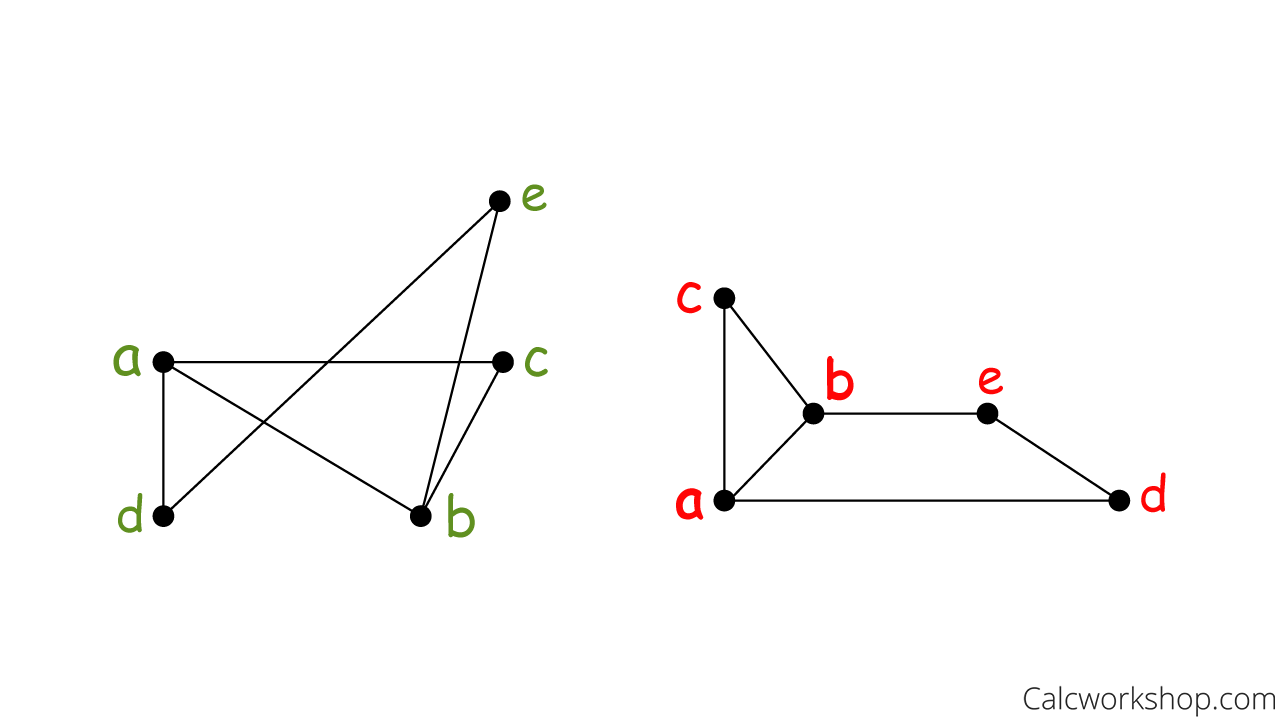
Label Remaining Vertices
And finally, we define our isomorphism by relabeling each graph and verifying one-to-correspondence.

Define Isomorphism — Example
Relabeling Caveats
Please know that this is not the only way to define the isomorphism as if graph G has n vertices and graph H has m edges. The number of bijections from vertices is n! and the number of bijections from edges is m! so the total number of pairs of functions to check is (n!)(m!)
Goodness gracious, that’s a lot of possibilities. And because there’s no efficient or one-size-fits-all approach for checking whether two graphs are isomorphic, the best method is to determine if a pair is not isomorphic instead…check the vertices, edges, and degrees!
For example, let’s show the next pair of graphs is not an isomorphism.
The first thing we do is count the number of edges and vertices and see if they match. Then we look at the degree sequence and see if they are also equal. Next, we look for the longest cycle as long as the first few questions have produced a matching result. And lastly, we will relabel, using method 2, to generate our isomorphism.
For the following two examples, you will see that the degree sequence is the best way for us to determine if two graphs are isomorphic.

Degree Sequence — Isomorphic

Degree Sequence — Not Isomorphic
Connectivity
Now we’re going to dig a little deeper into this idea of connectivity.
In our previous lesson, Graph Theory, we talked about subgraphs, as we sometimes only want or need a portion of a graph to solve a problem. If removing a vertex or an edge from a graph produces a subgraph, are there times when removing a particular vertex or edge will create a disconnected graph?
The removal of a cut vertex, sometimes called cut points or articulation points, and all its adjacent edges produce a subgraph that is not connected. Likewise, removing a cut edge, commonly called a bridge, also makes a disconnected graph. The key to determining cut points and bridges is to go one vertex or edge at a time. If you remove it, can you still chart a path to all remaining vertices? If the answer is no, then it’s a cut point or edge.
Example
Determine all cut point or articulation vertices from the graph below:

Identify Cut Points — Example
Notice that if we remove vertex “c” and all its adjacent edges, as seen by the graph on the right, we are left with a disconnected graph and no way to traverse every vertex.
Example
Find all bridges from the graph below.

Identify Bridge — Example
Notice that by removing edge {c,d} as seen on the graph on the right, we are left with a disconnected graph
But sometimes, we don’t want to remove an edge but relocate it. A graph is planar if it can be drawn in the plane without any edges crossing. In other words, edges only intersect at endpoints (vertices)
For example, the following graph is planar because we can redraw the purple edge so that the graph has no intersecting edges.
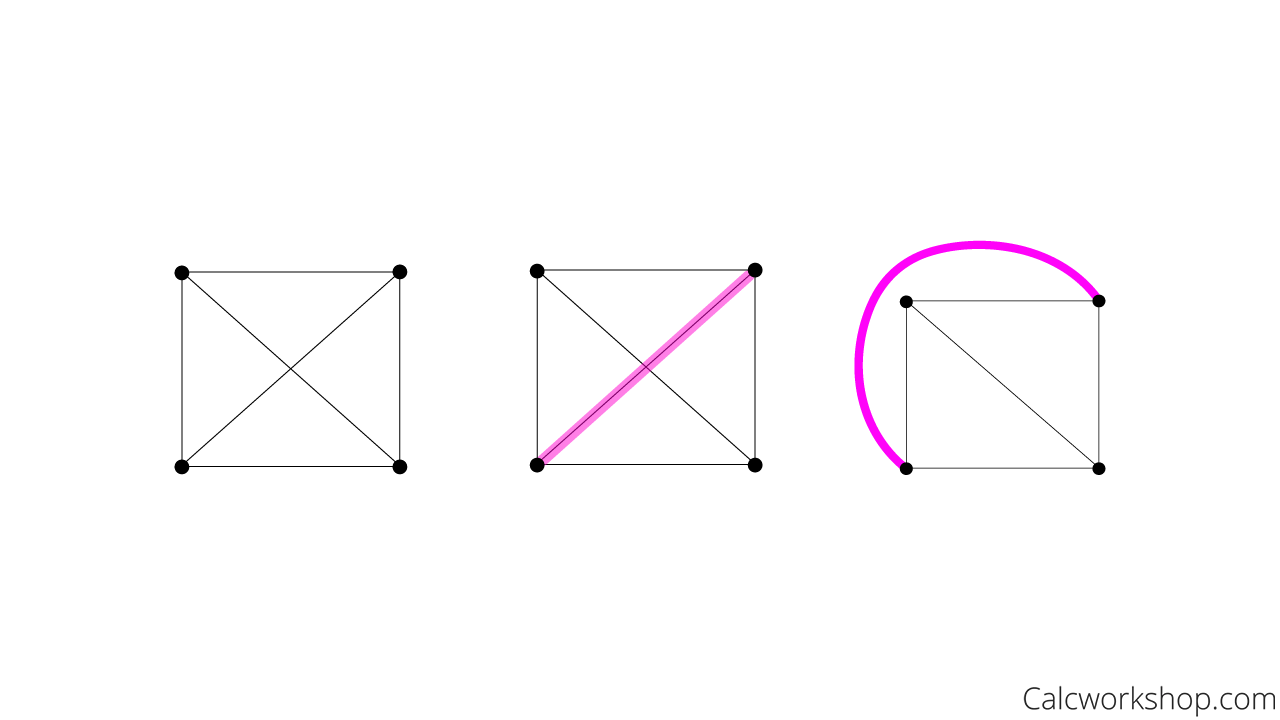
Planar Graph — Example
Quotient Graphs
Lastly, let’s discuss quotient graphs.
A quotient graph can be obtained when you have a graph G and an equivalence relation R on its vertices. The new graph has a vertex for each equivalence class and an edge whenever there is an edge in G connecting a vertex from each of these equivalence classes. These can be a bit tricky at first, but we will work through these questions slowly in the video to ensure understanding.
Together we will learn how to determine if two graphs are isomorphic, find bridges and cut points, identify planar graphs, and draw quotient graphs.
Let’s get to it.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.