Did you know that graph theory got its start around the 18th century when Leonhard Euler found the solution to the seven bridges of Konigsberg problem?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Background
Legend has it that the citizens of Konigsberg, Prussia, now modern-day Kalingrad, Russia, which is home to seven bridges that cross over the Pregel River, wanted to know if it was possible to traverse each of the seven bridges exactly once, without doubling back.
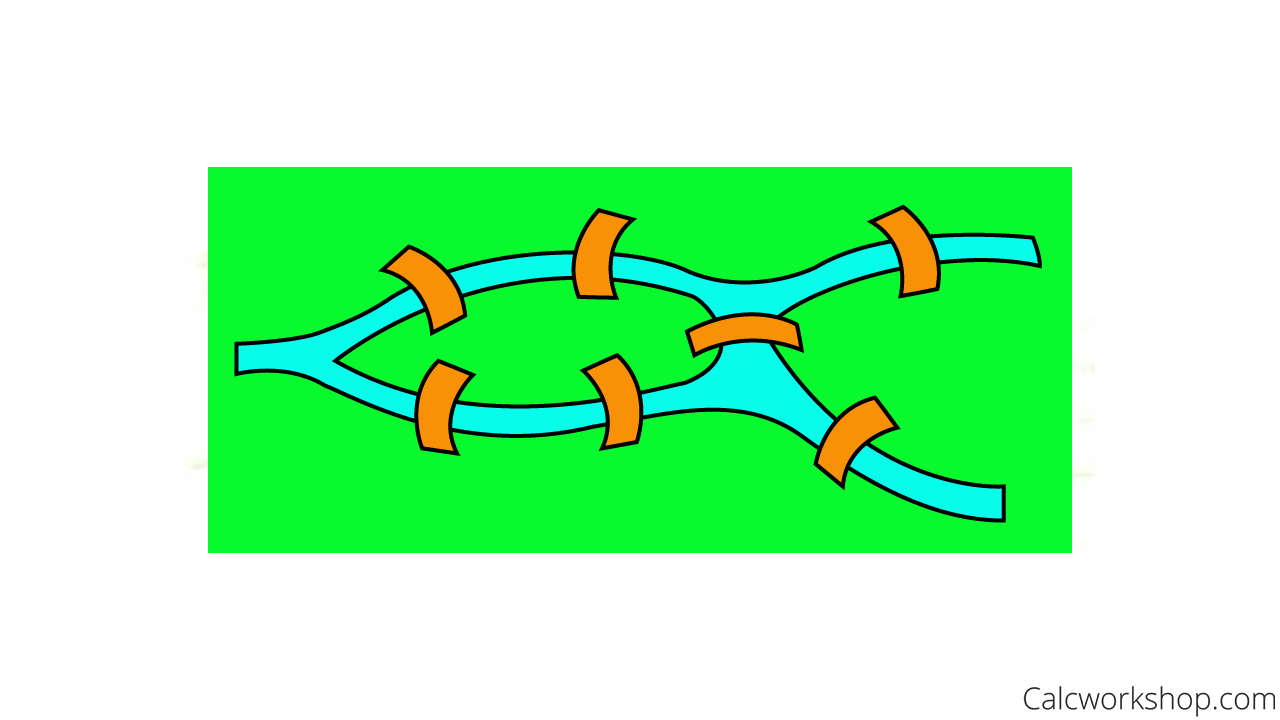
Konigsberg Bridge Problem
Euler was intrigued by the question and solved the problem by visualizing the bridges as a network or a graph.
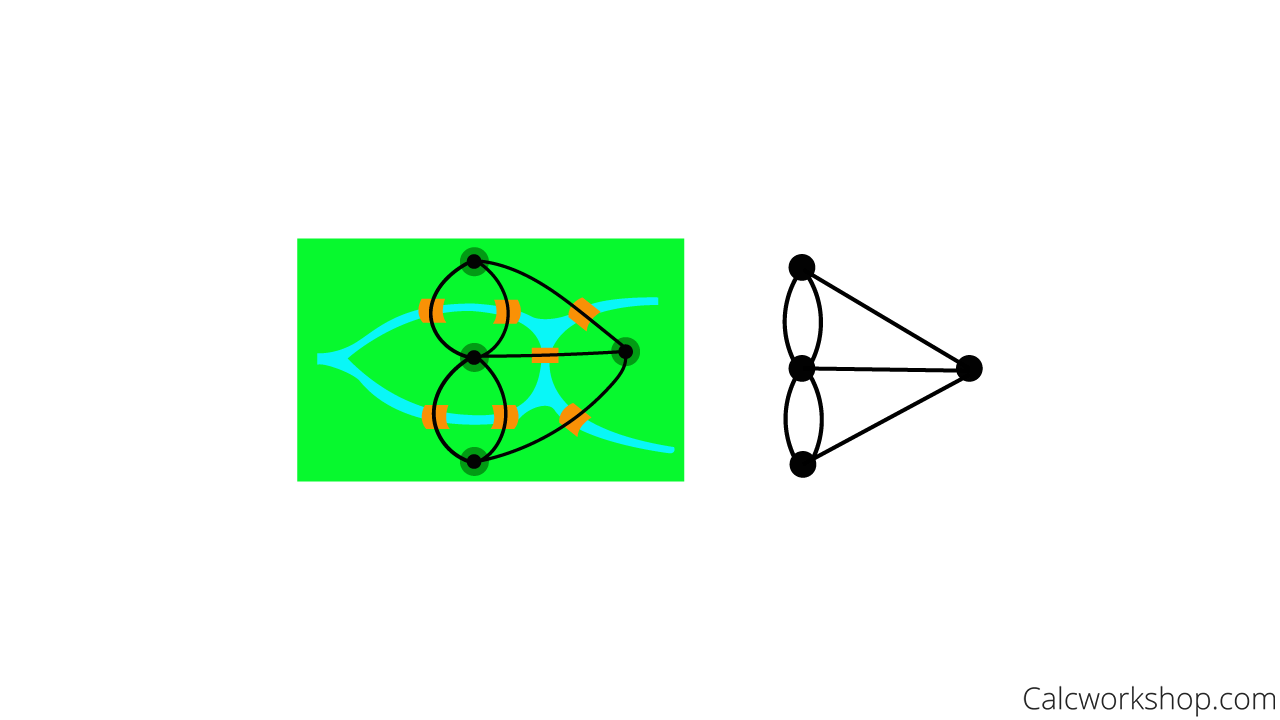
Graph Theory Bridge Problem
Euler Circuit
He concluded that it was impossible to cross all seven bridges exactly once, and his solution and approach is the foundation of modern-day graph theory.
Let’s look closely at his conclusions.
- An Euler path (trail) is a path that traverses every edge exactly once (no repeats). This can only be accomplished if and only if exactly two vertices have odd degree, as noted by the University of Nebraska.
- An Euler circuit (cycle) traverses every edge exactly once and starts and stops as the same vertex. This can only be done if and only if every vertex has an even degree. An Euler circuit is automatically an Euler path.
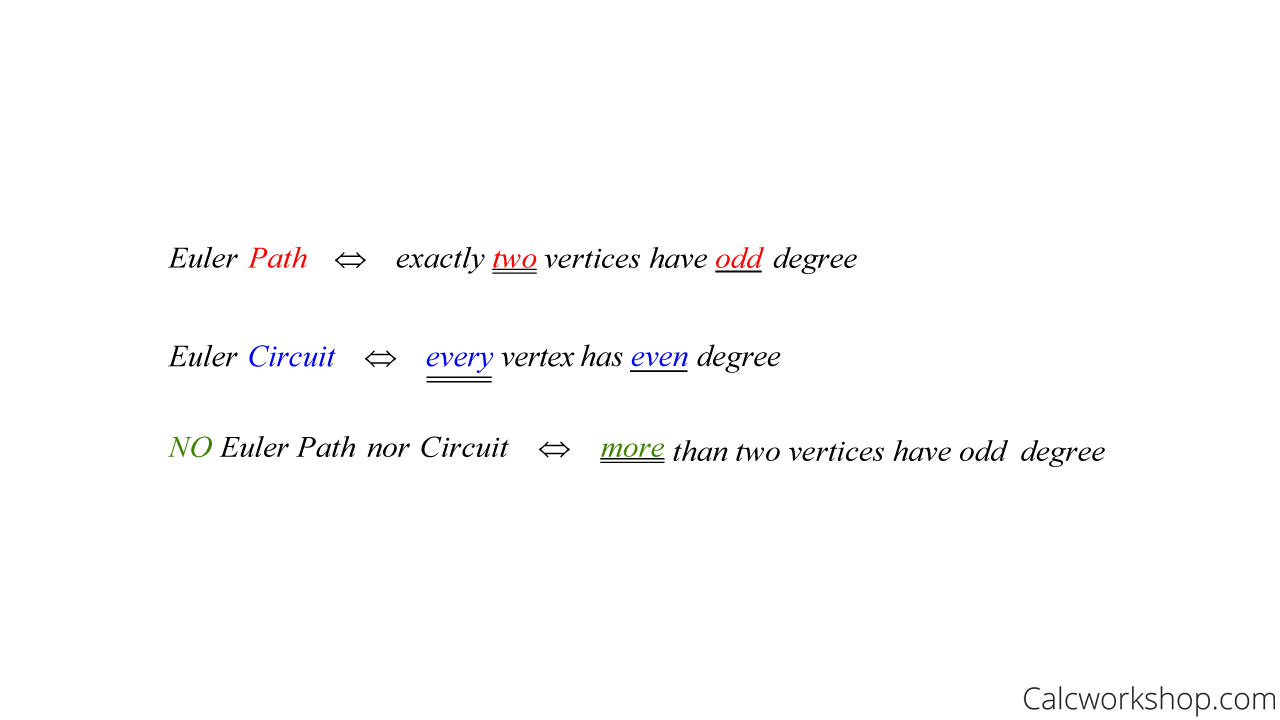
Euler Path Vs Circuit
Consequently, for the seven bridges of Konigsberg, it is neither a path nor a circuit because three vertices are of odd degree.
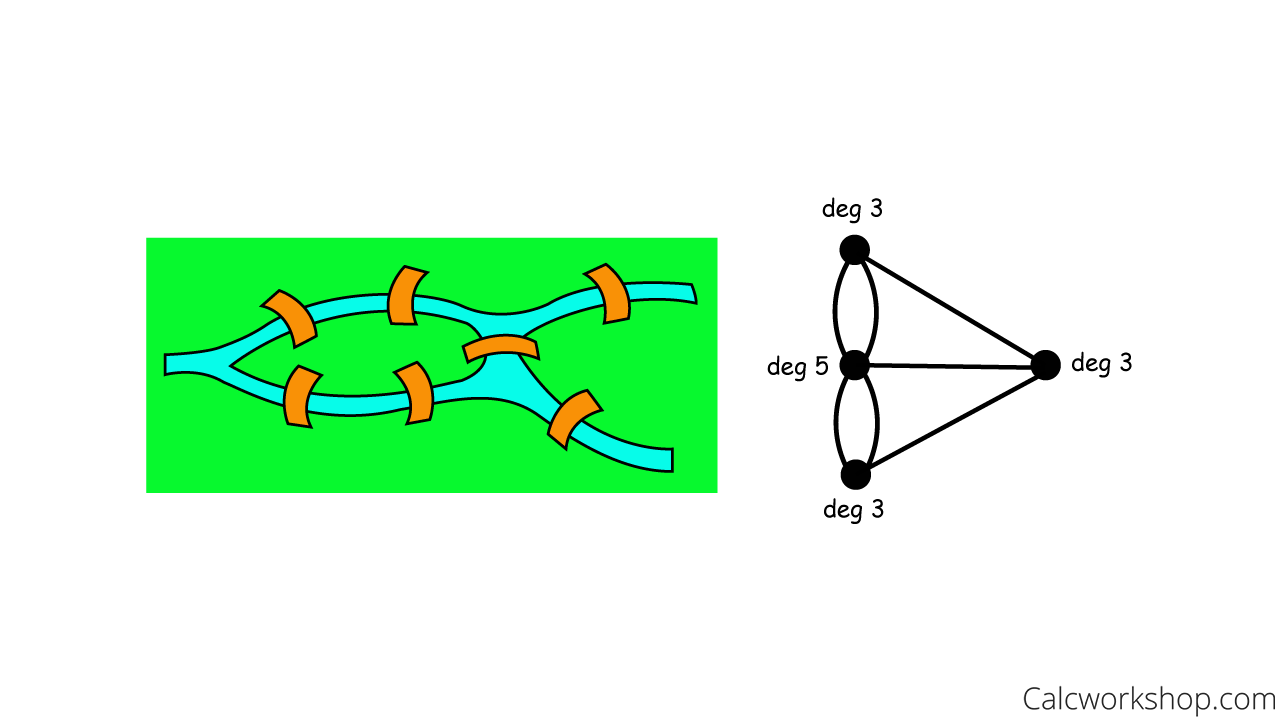
Solution Euler Bridge
So, let’s take our Euler Graph Theorems and use them to see if we can determine if the following graph creates an Euler circuit, path, or neither.
Example – Euler Circuit

Euler Circuit Example
Example – Euler Path

Euler Path Example
Example – Neither Path nor Circuit

Neither Euler Path Circuit Example
Fleury’s Algorithm
Additionally, suppose we can determine that every vertex is even or there are exactly two odd vertices. In that case, we can use Fleury’s Algorithm to find an Eulerian circuit (cycle) or path.
Here’s how Fleury’s algorithm works:
First, if every vertex is even, then start anywhere, but if there are two odd vertices, pick one of them to start at.
Second, from that vertex, pick an edge to traverse, but know that you can’t go back once you traverse the edge, so don’t cross a bridge unless there’s no other choice.
Remember, a bridge is an edge that, if removed it produces a disconnected graph, and we want to be able to traverse the entire graph without picking up our pencil, so we need to be careful not to “burn bridges” because once it’s gone, there is no going back.
Third, keep going until you run out of edges. If you are finding an Euler Circuit, you should be back to where you started.
Example
Let’s look at an example. Use Fleury’s algorithm to find an Euler path for the graph below.

How To Find A Euler Circuit
Knowing that we need to start at either of the two odd vertices (B or E), let’s pick E to start. And we start crossing edges, knowing that as soon as we cross an edge, we need to remove (burn) it.

Fleury Algorithm Euler Circuit Example
But now we run into a problem — if we cross edge CB, we would be stuck with no way of getting to the other vertices. This means we can’t burn the bridge CB, so we need to choose a different path, so let’s traverse CD instead.

Fleury Algorithm Bridge Example
Now we can continue on our path until we reach the other odd degree vertex.

Complete Fluery Algorithm Example
This means using Fleury’s Algorithm, we found an Euler path: EABFCDEFDCB
Hamilton Paths
Alright, so now it’s time to look at Hamilton graphs. While Euler graphs focus on edges, saying you can only visit an edge exactly once, Hamilton graphs focus on vertices and say we can only visit a vertex exactly once.
This means that Hamilton paths traverse every vertex exactly once, and a Hamilton circuit (cycle) traverses every vertex once and begins and ends at the same node.
While there isn’t a general formula for determining a Hamilton graph, besides guess and check, we can be assured that there is no Hamilton circuit if there is a vertex of degree 1.
Okay, so let’s see if we can determine if the following graphs are Hamiltonian paths, circuits, or neither.

Hamilton Path Circuit Example
Traveling Salesman
And there’s a very famous application to the Hamiltonian graph called the Traveling Salesman (salesperson) problem, sometimes called a TSP problem. The question states that given a list of cities and distances between each pair of cities, what is the shortest possible route that will visit each city exactly once and returns to the original city?
What is important to notice about this question is that it doesn’t matter if we traverse every road, only that we make it to each city (vertex) once and get back to where we started. So, all we have to do is find a Hamiltonian Circuit!
The following graph shows four cities and the distances between each pair of cities. Let’s solve the TSP problem, starting at city A, using the brute-force method where we list all the possible tours, and the shortest tour is the optimal one.

Traveling Salesman Problem
So, the optimal tour would be either ACBDA OR ADBCA, as they both have a total cost of 80.
In graph theory, the distances are called weights, and the path of minimum weight or cost is the shortest.
Together we will learn how to find Euler and Hamilton paths and circuits, use Fleury’s algorithm for identifying Eulerian circuits, and employ the shortest path algorithm to solve the famous Traveling Salesperson problem.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.