What are the Reflection Rules?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
That’s what today’s geometry lesson is all about.
You’re going to learn how to find the line of reflection, graph a reflection in a coordinate plane, and so much more.
So let’s get started!
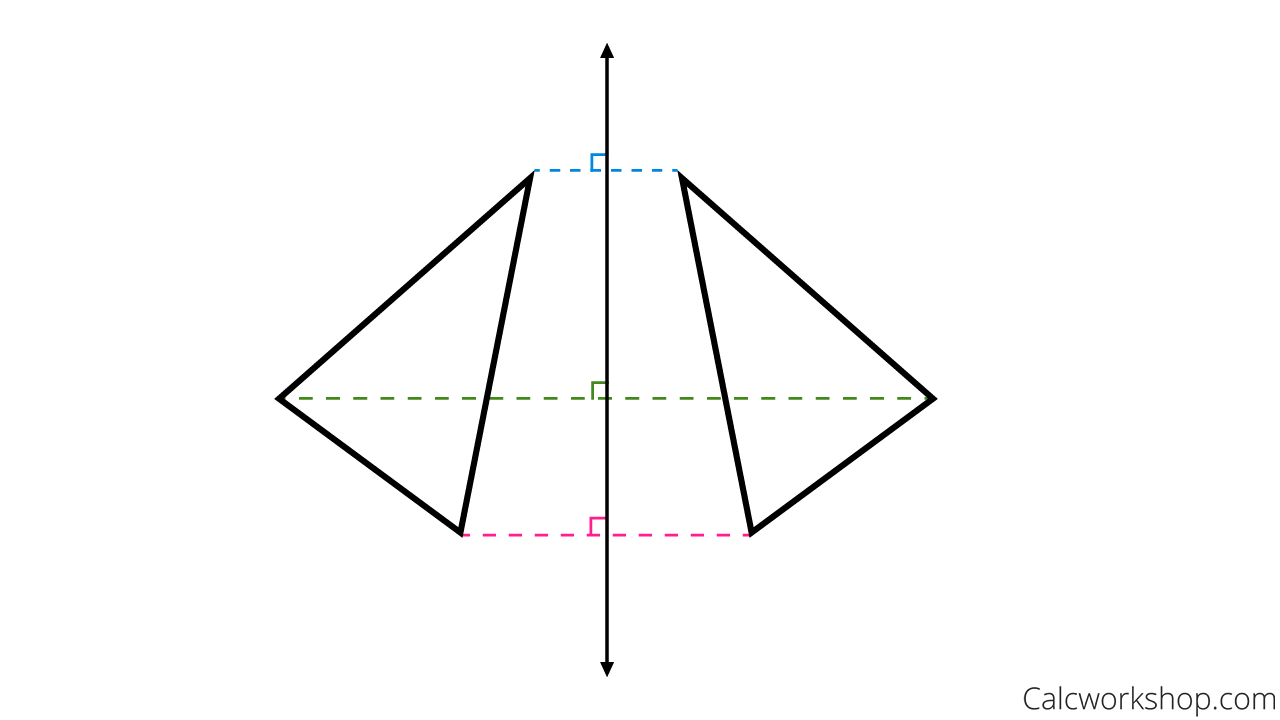
A transformation that uses a line that acts as a mirror, with an original figure (preimage) reflected in the line to create a new figure (image) is called a reflection.
A reflection is sometimes called a flip or fold because the figure is flipped or folded over the line of reflection to create a new figure that is exactly the same size and shape.
Reflection Example
What is important to note is that the line of reflection is the perpendicular bisector between the preimage and the image. Thus ensuring that a reflection is an isometry, as Math Bits Notebook rightly states.
Reflection on a Coordinate Plane
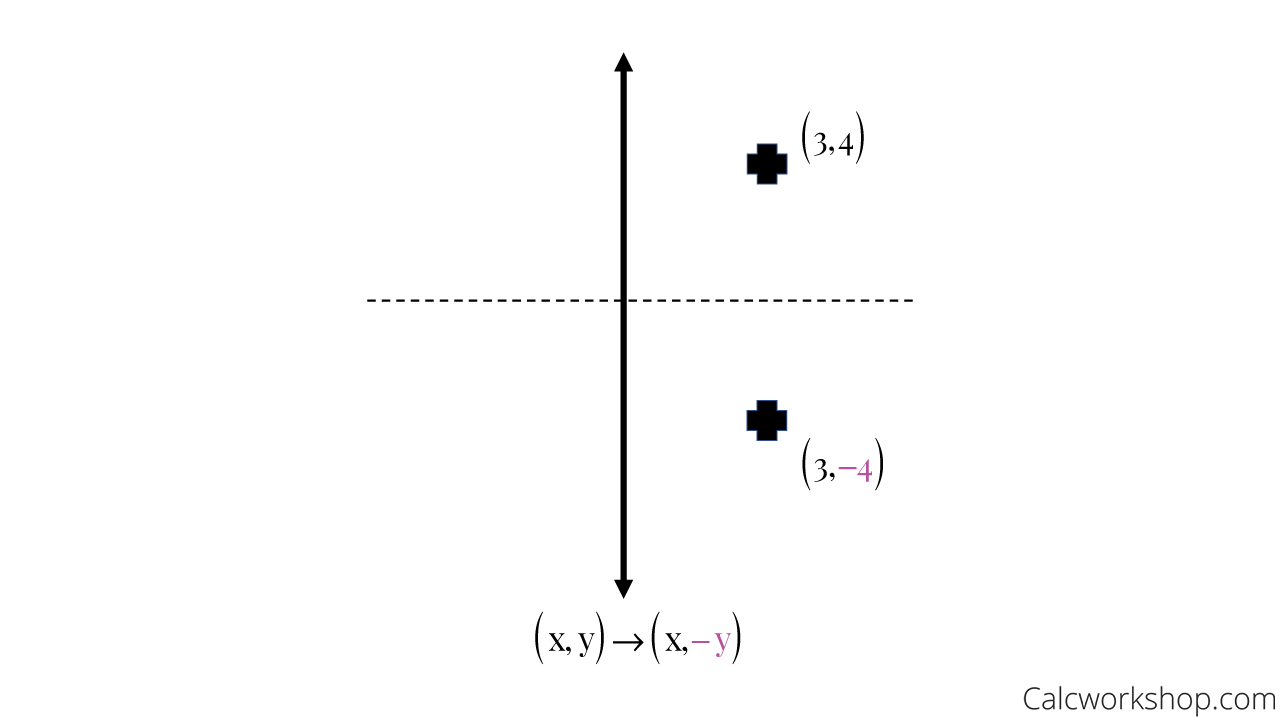
Reflection Over X Axis
When reflecting over (across) the x-axis, we keep x the same, but make y negative.
Reflection Across the X-Axis
Reflection Over Y Axis
When reflecting over (across) the y-axis, we keep y the same, but make x-negative.
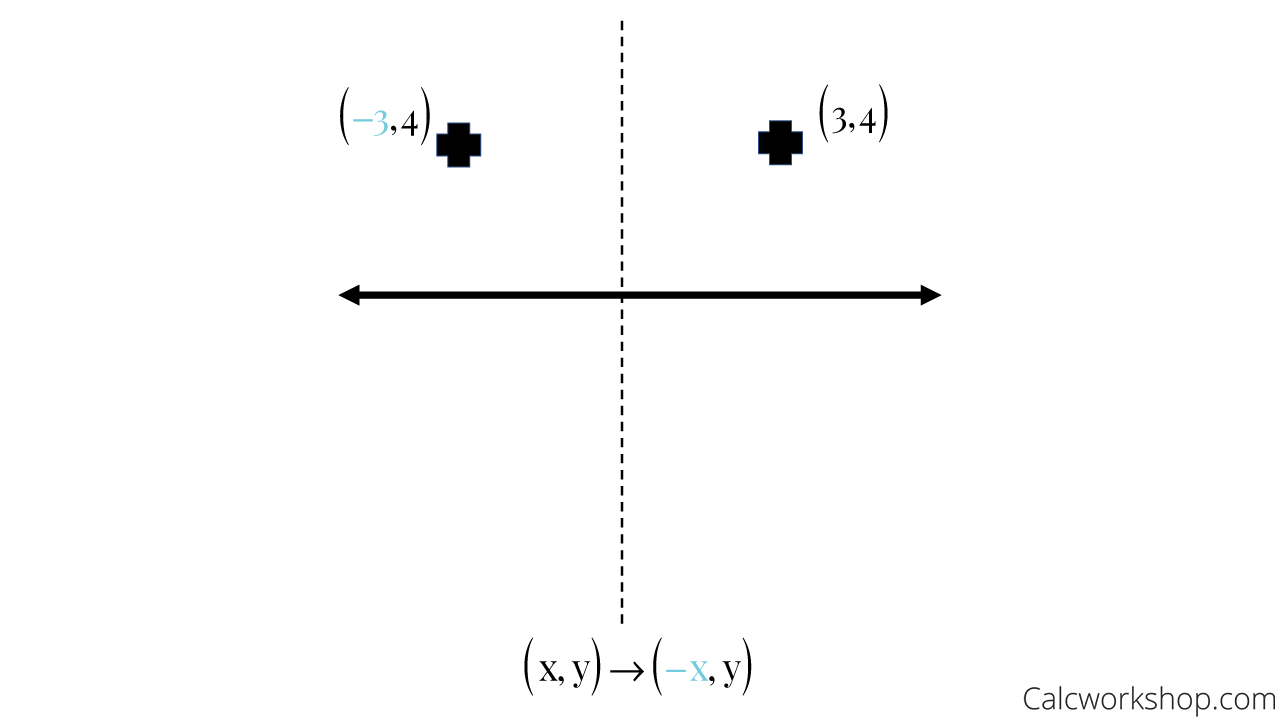
Reflection Across the Y-Axis
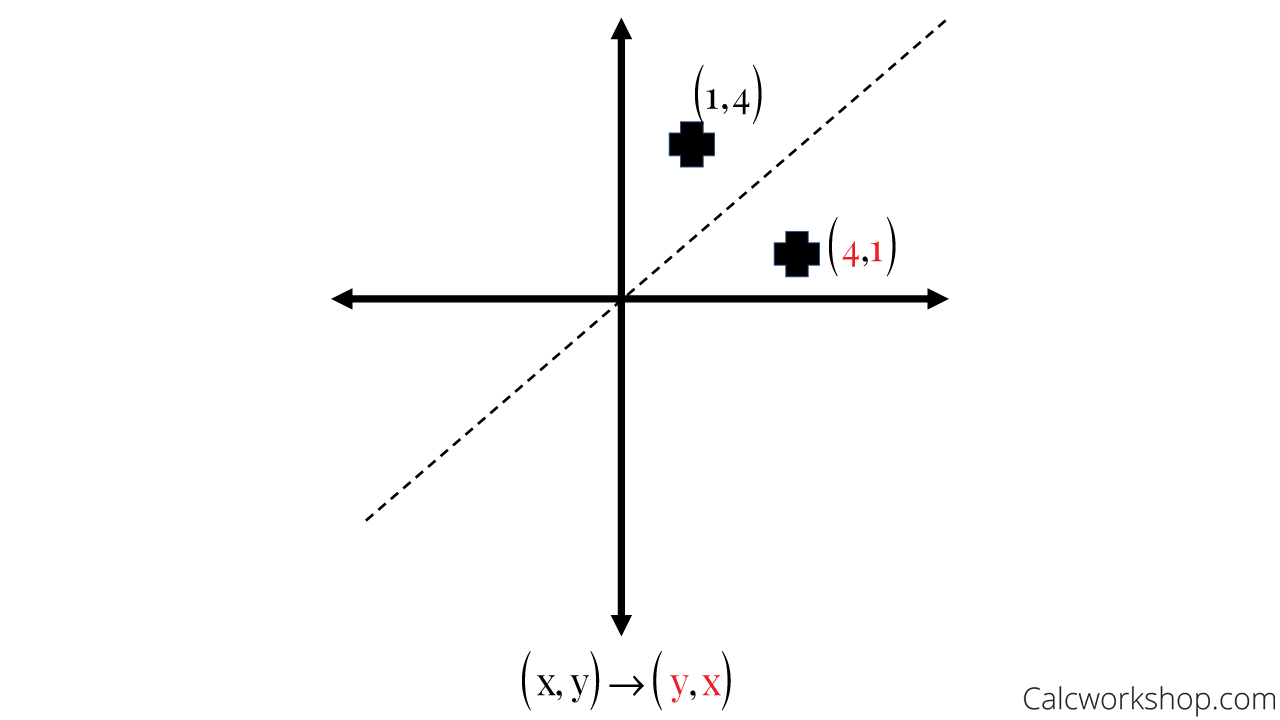
Reflection Across Y=X
When reflecting over the line y=x, we switch our x and y. These reflected points represent the inverse function.
Reflection Over Y=X
Reflection Across Y=-X
When reflecting over the line y=-x, we switch our x and y, and make both negative.
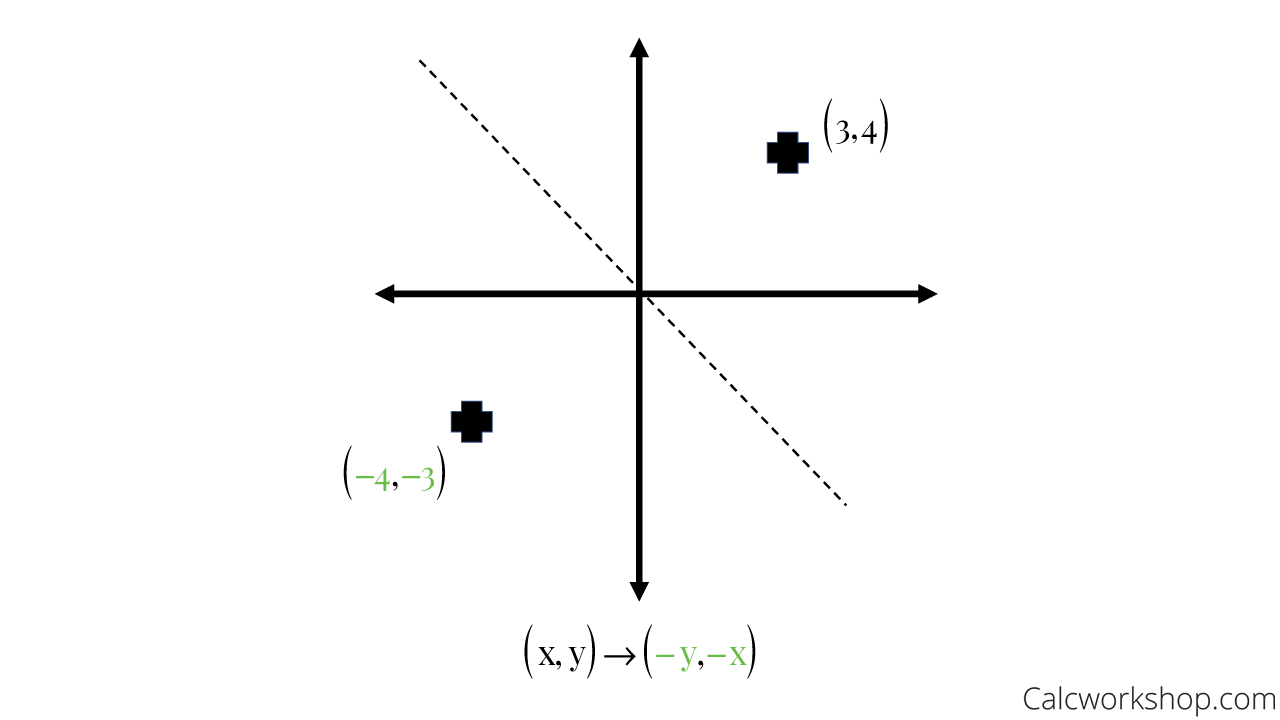
Reflection Over Y = -X
In order to define or describe a reflection, you need the equation of the line of reflection. The four most common reflections are defined below:
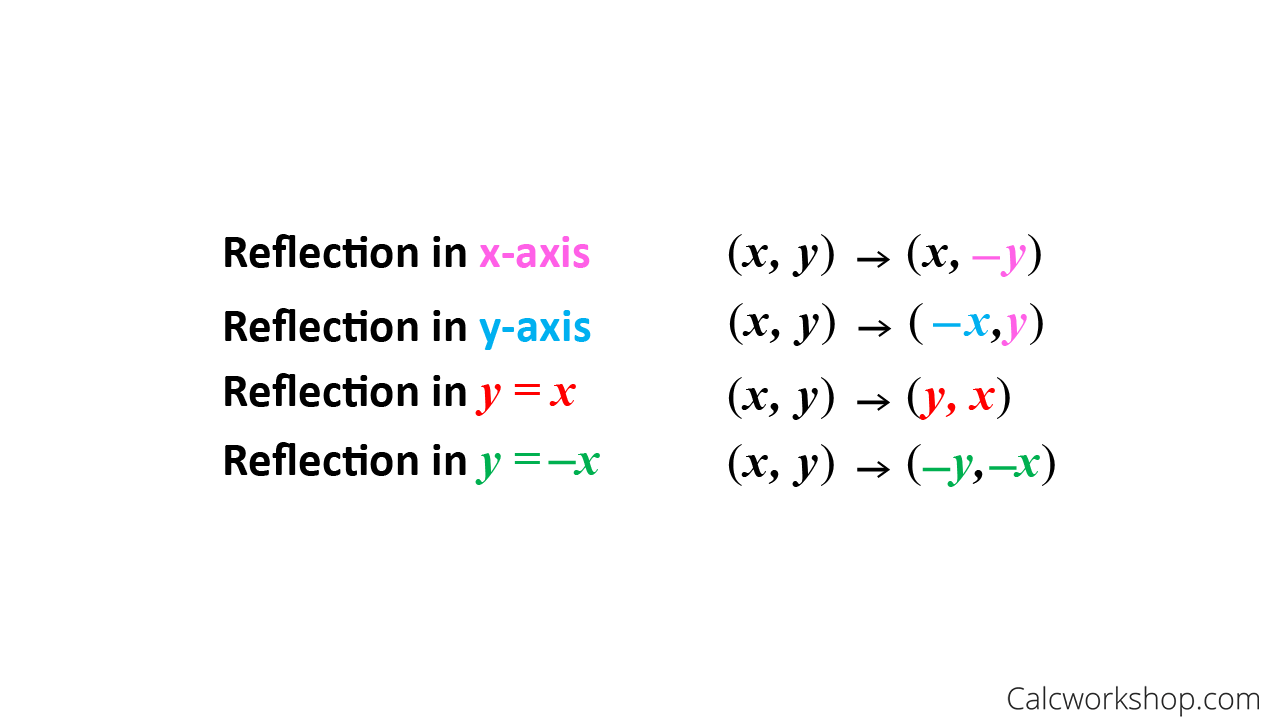
Common Reflections About the Origin
Reflection Symmetry
Additionally, symmetry is another form of a reflective transformation. When a figure can be mapped (folded or flipped) onto itself by a reflection, then the figure has a line of symmetry.
For example, the image of a heart has one line of symmetry, as we can fold the heart in half to create the same shape. Similarly, the example of the equilateral triangle below has three lines of symmetry, as we can fold the triangle along these lines to create equal halves.

1 Line of Symmetry

3 Lines of Symmetry
Glide Reflection
A glide reflection is a composite transformation where we translate (glide) and then reflect a figure in successive steps. But what is super cool about glide reflections is that as long as the translation is parallel to the line of reflection, it doesn’t matter which transformation you perform first. So that means we can slide then flip, or we can flip then slide.
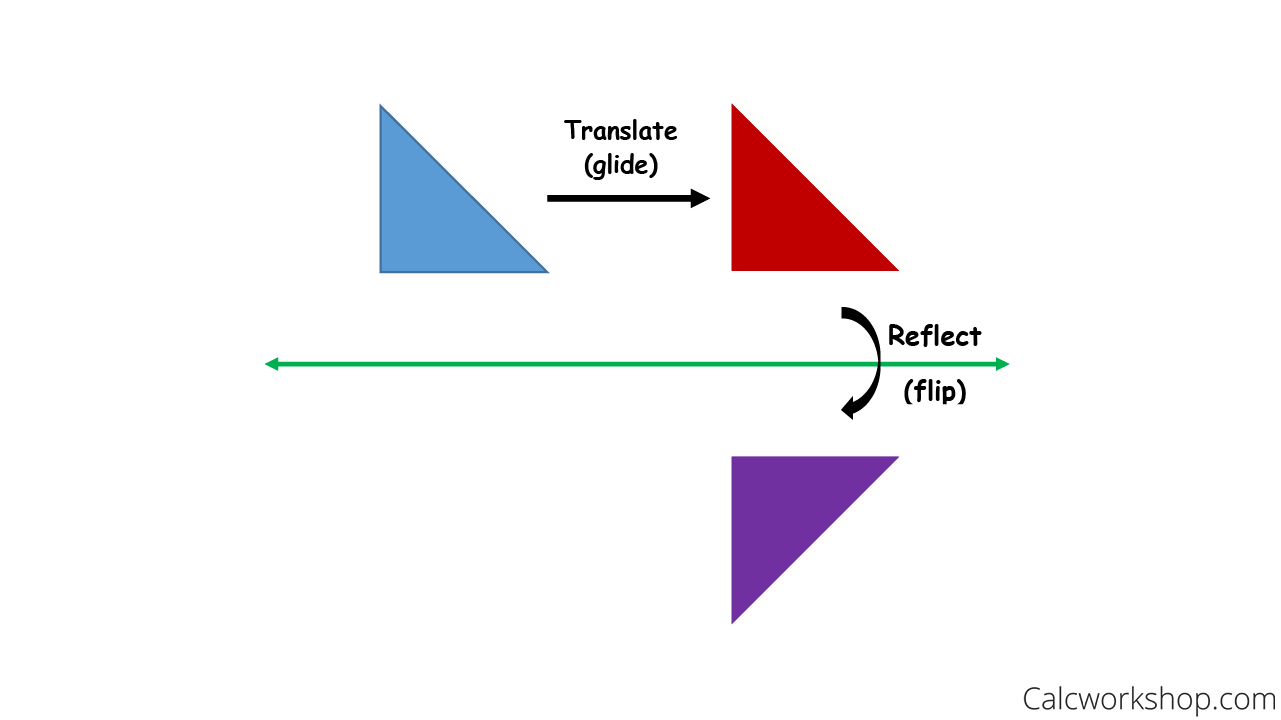
Glide Reflection Examples
And did you know that reflections are used to help us find minimum distances?
Now we all know that the shortest distance between any two points is a straight line, but what would happen if you need to go to two different places?
For example, imagine you and your friend are traveling together in a car. You need to go to the grocery store and your friend needs to go to the flower shop. Where should you park the car minimize the distance you both will have to walk?
The answer is found using reflections!
Next, you’ll learn how to:
- Draw reflections.
- Describe the reflection by finding the line of reflection.
- Determine the number of lines of symmetry.
- Find a point on the line of reflection that creates a minimum distance.
Video – Lesson & Examples
58 min
- Introduction to Reflections
- 00:00:43 – Properties of Reflections: Graph and Describe the Reflection (Examples #1-4)
- Exclusive Content for Member’s Only
- 00:10:53 – How to find the line of reflection (Examples #5-7)
- 00:17:45 – Graph the given reflection in the coordinate plane (Examples #8-13)
- 00:25:02 – Determine the number of lines of symmetry (Examples #14-17)
- 00:30:22 – Determine how a square piece of paper will look once unfolded (Examples #18-20)
- 00:35:42 – Glide Reflections and the Composition Theorem (Examples #21-22)
- 00:44:53 – Overview of how we can Optimize with Geometry
- 00:52:16 – Finding the minimum distance using reflections (Examples #23-25)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.