Quadratic Form (Matrix Approach for Conic Sections)

Picture yourself playing a game of Clue, where the objective is to solve a mystery involving quadratic forms and conic sections.

Jenn (B.S., M.Ed.) of Calcworkshop® teaching quadractic forms

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

In Clue, players gather evidence and deduce the hidden truth behind the crime by identifying the who, where, and with what weapon.

Similarly, in our quadratic forms investigation, we’ll use linear algebra techniques to reveal the hidden conic sections within the equations by identifying their shape, orientation, and transformation properties.

So grab your detective hat and let’s start our investigation with the matrix representation of quadratic forms.

Matrix Representation of Quadratic Forms

A quadratic form is a function Q defined on $R^{n}$ such that $Q : R^{n} \to R$ that can be written in the form $Q (x) = x^{T} A x$ , where A is a symmetric matrix and is called the matrix of the quadratic form.

But first, we need to make a connection between the quadratic form and its associated symmetric matrix.

When given a quadratic function, we place the coefficient of each squared term down the main diagonal, and half of each cross-product term split symmetrically.

Examples: Finding the Matrix of Quadratic Forms

For example, let’s find the matrix of the quadratic form:

$a x_{1}^{2} + b x_{1} x_{2} + c x_{2}^{2} \Rightarrow [\begin{array}{cc} a & \frac{b}{2} \\ \frac{b}{2} & c \end{array}]$

$- 5 x_{1}^{2} + 8 x_{1} x_{2} + 9 x_{2}^{2} \Rightarrow [\begin{array}{cc} - 5 & 4 \\ 4 & 9 \end{array}]$

$3 x_{1}^{2} + - 4 x_{1} x_{2} + 6 x_{2}^{2} \Rightarrow [\begin{array}{cc} 3 & - 2 \\ - 2 & 6 \end{array}]$

$8 x_{1}^{2} + 7 x_{2}^{2} + - 3 x_{3}^{2} + - 6 x_{1} x_{2} + 4 x_{1} x_{3} + - 2 x_{2} x_{3} \Rightarrow [\begin{array}{ccc} 8 & - 3 & 2 \\ - 3 & 7 & - 1 \\ 2 & - 1 & - 3 \end{array}]$

And with this knowledge, we can reverse this process by computing $x^{T} A x$

For example, if we are given the symmetric matrix $[\begin{array}{cc} 3 & - 2 \\ - 2 & 7 \end{array}]$ we can write the quadratic form as follows.

$x^{T} A x = [\begin{array}{ll} x_{1} & x_{2} \end{array}] [\begin{array}{cc} 3 & - 2 \\ - 2 & 7 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}]$

$\Rightarrow 3 x_{1} x_{1} - 2 x_{1} x_{2} - 2 x_{2} x_{1} + 7 x_{2} x_{2}$

$\Rightarrow 3 x_{1}^{2} - 4 x_{1} x_{2} + 7 x_{2}^{2}$

See, it’s easy. Don’t worry; we’ll work through numerous examples in the video to help make sense of this process.

While this is great, what’s the point?

Back in Algebra 2 or Precalculus, we learned about conic sections:

Parabola
Circle
Ellipse
Hyperbola

But all of the conics we studied could be graphed on the xy-plane as they contained no cross-product terms.

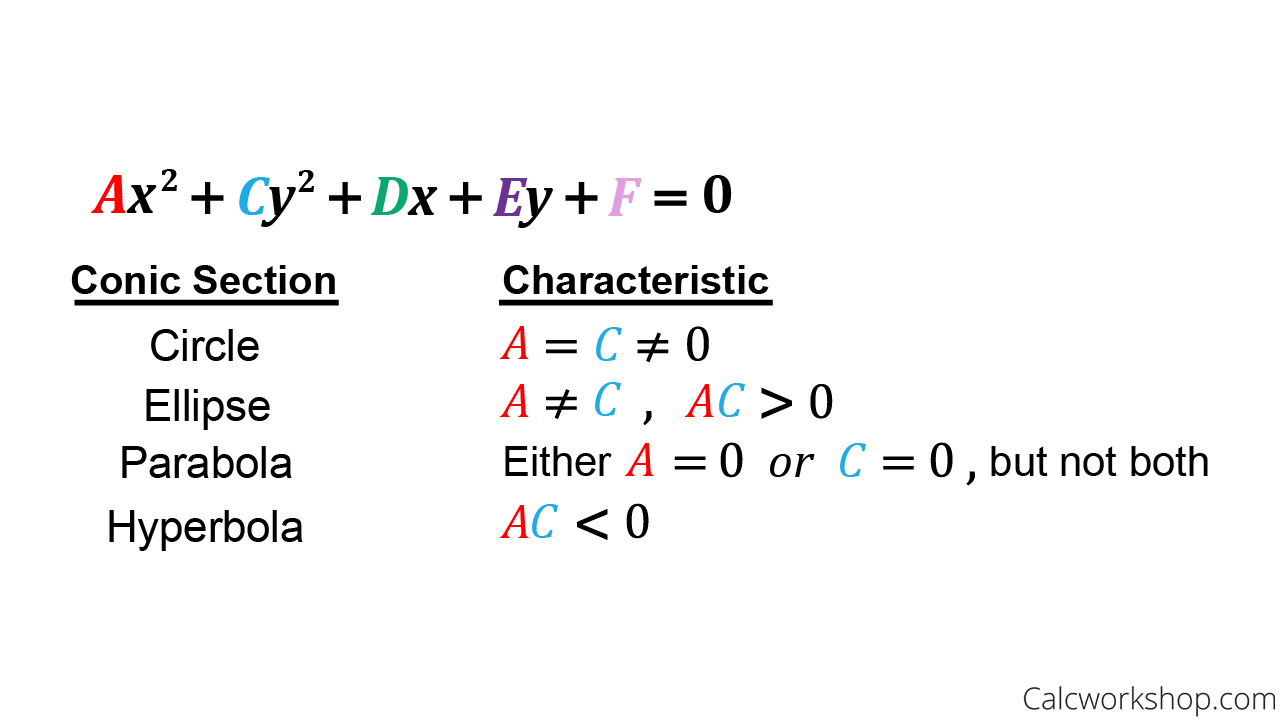
Important characteristics of all conic sections

Conic Section Properties

Change of Variables in Quadratic Forms

What do we do if our conic section does have a cross product term? How can we identify it and subsequently graph it?

Ahh, this is why we need matrices and a technique called the change of variable in a quadratic form!

If $\vec{x}$ represents a variable vector in $R^{n}$ , then a change of variable is an equation of the form $\vec{x} = P \vec{y}$ or $\vec{y} = P^{- 1} \vec{x}$

Where $P$ is an invertible matrix that orthogonally diagonalizes matrix $A$ and $\vec{y}$ is a new variable vector in $R^{n}$ .

Principal Axis Theorem

This leads us directly to the Principal Axis Theorem, which states that if we let A be a square $n \times n$ matrix, then there is an orthogonal change of variable, $\vec{x} = \vec{P}$ , that transforms the quadratic form $x^{T} A x$ into a quadratic form $y^{T} D y$ with no cross-product term. And the columns of $P$ are called the principal axes and determine the axis of rotation.

Confused?

Steps for Making a Change of Variables

Don’t fear. Here are the steps for making a change of variables:

Make the matrix A of the quadratic form like we did for the examples above.
Find eigenvalues by solving the characteristic equation.
Identify each eigenspace (i.e., find the eigenvectors that correspond to each eigenvalue)
Check for orthogonality, and if necessary, apply the Gram-Schmidt process
Normalize to create matrix $P$ that is orthonormal
Write $P$ and $D$ matrices and use them to create the transformed quadratic equation without cross-product terms and identify the quadratic form.

Example: Transforming Quadratic Forms

Let’s look at an example.

Transform the quadratic form $Q (x) = 8 x_{1}^{2} + 6 x_{1} x_{2}$ into one with no cross-product term.

First, we will find the matrix of the quadratic form like we did for the examples above.

$Q (x) = 8 x_{1}^{2} + 6 x_{1} x_{2}$

$\Rightarrow Q (x) = 8 x_{1}^{2} + 6 x_{1} x_{2} + 0 x_{2}^{2}$

$\Rightarrow [\begin{array}{ll} 8 & 3 \\ 3 & 0 \end{array}]$

Next, we will find our eigenvalues.

$\begin{array}{r} \begin{aligned} \det [\begin{array}{cc} 8 - λ & 3 \\ 3 & 0 - λ \end{array}] = 0 \\ (8 - λ) (0 - λ) - (3) (3) = 0 \\ λ^{2} - 8 λ - 9 = 0 \\ (λ - 9) (λ + 1) = 0 \\ λ = 9, - 1 \end{aligned} \end{array}$

Now, we will find the basis for the eigenspace associated with each eigenvector.

$λ = 9 \Rightarrow [\begin{array}{ccc} - 1 & 3 & 0 \\ 3 & - 9 & 0 \end{array}] \sim [\begin{array}{ccc} 1 & - 3 & 0 \\ 0 & 0 & 0 \end{array}]$

$\Rightarrow \vec{x} = [\begin{array}{l} 3 \\ 1 \end{array}]$

$λ = - 1 \Rightarrow [\begin{array}{lll} 9 & 3 & 0 \\ 3 & 1 & 0 \end{array}] \sim [\begin{array}{ccc} 1 & 1 / 3 & 0 \\ 0 & 0 & 0 \end{array}]$

$\Rightarrow \vec{x} = [\begin{matrix} - 1 / 3 \\ 1 \end{matrix}] or \vec{x} = [\begin{matrix} - 1 \\ 3 \end{matrix}]$

Okay, so now that we have our two eigenvectors, we must verify that they are orthogonal.

$\begin{array}{r} \underset{v_{1}}{\underset{⏟}{[\begin{array}{l} 3 \\ 1 \end{array}]}} \underset{v_{2}}{\underset{⏟}{[\begin{array}{c} - 1 \\ 3 \end{array}]}} v_{1} \cdot v_{2} = 0 \end{array}$

Now, it is time to normalize our vectors to create an orthonormal $P$ matrix.

$‖ v_{1} ‖ = \sqrt{(3)^{2} + (1)^{2}} = \sqrt{10}$

$\Rightarrow u_{1} = \frac{1}{\sqrt{10}} [\begin{array}{l} 3 \\ 1 \end{array}]$

$= [\begin{matrix} 3 / \sqrt{10} \\ 1 / \sqrt{10} \end{matrix}]$

$‖ v_{2} ‖ = \sqrt{(- 1)^{2} + (3)^{2}} = \sqrt{10}$

$\Rightarrow u_{2} = \frac{1}{\sqrt{10}} [\begin{matrix} - 1 \\ 3 \end{matrix}]$

$= [\begin{matrix} - 1 / \sqrt{10} \\ 3 / \sqrt{10} \end{matrix}]$

$P = [\begin{array}{cc} 3 / \sqrt{10} & - 1 / \sqrt{10} \\ 1 / \sqrt{10} & 3 / \sqrt{10} \end{array}], D = [\begin{array}{cc} 9 & 0 \\ 0 & - 1 \end{array}]$

And remembering that $A = P D P^{- 1} = P D P^{T}$ from our previous lesson on symmetric matrices, we can verify our work as follows, knowing that the columns of $P$ are our principal axes.

$\begin{array}{r} [\begin{array}{ll} 8 & 3 \\ 3 & 0 \end{array}] = [\begin{array}{cc} 3 / \sqrt{10} & - 1 / \sqrt{10} \\ 1 / \sqrt{10} & 3 / \sqrt{10} \end{array}] [\begin{array}{cc} 9 & 0 \\ 0 & - 1 \end{array}] [\begin{array}{cc} 3 / \sqrt{10} & 1 / \sqrt{10} \\ - 1 / \sqrt{10} & 3 / \sqrt{10} \end{array}] \end{array}$

Lastly, we write our new quadratic form and identify the conic section.

$x^{T} A x = y^{T} D y$

$\Rightarrow [\begin{array}{ll} y_{1} & y_{2} \end{array}] [\begin{array}{cc} 9 & 0 \\ 0 & - 1 \end{array}] [\begin{array}{l} y_{1} \\ y_{2} \end{array}]$

$= 9 y_{1} y_{1} - y_{2} y_{2} \Rightarrow \underset{Hyperbola}{\underset{⏟}{9 y_{1}^{2} - y_{2}^{2}}}$

And that’s all we have to do to transform the quadratic form!

Identifying Quadratic Forms

Now, there are some other important properties to know when identifying a quadratic form $Q$ .

A quadratic form $Q$ is:

Positive definite if $Q (x) > 0$ for all $\vec{x} \neq \vec{0}$ (i.e., the eigenvalues of $A$ are all positive)
Negative definite if $Q (x) < 0$ for all $\vec{x} \neq \vec{0}$ (i.e., the eigenvalues of $A$ are all negative)
Indefinite if $Q (x)$ assumes both positive and negative values. (i.e., the eigenvalues of $A$ are both positive and negative)

If $λ_{1} \cdot λ_{2} > 0$ , then the quadratic form after the change of variables will be an ellipse or a circle.

If $λ_{1} \cdot λ_{2} < 0$ , then the quadratic form after the change of variables will be a hyperbola.

If only one $λ$ , then the quadratic form after the change of variables will be a parabola.

Next Steps

There’s a lot to unpack in this lesson. You’ll work through examples step-by-step as you learn how to:

Compute the quadratic form
Find the matrix for the quadratic form
Classify the quadratic form
Use a change of variables to eliminate cross-product terms

Let’s get started!

Video Tutorial w/ Full Lesson & Detailed Examples

matrix-of-the-quadratic-form-example

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.

4.9 / 5

1,133 Reviews

Gina K.03-30-25 - WA, United States

My experience was great! I needed help studying for my math class, but I wasn't sure how-until an ad for this popped up on my YouTube. After watching the ad, I was convinced, so I subscribed to CalcWoskop. I'm so happy I did because it helped me so much with my class! I learned a lot that I couldn't grasp from my college lectures, and this was the perfect solution.

Serafimk2203-28-25 - NJ, United States

I had an Amazing experience with discrete math and calculus series. Graduating with highest honors thanks to calc workshop. I'll be back on the site again but this time if I need to go back as reference as well as if I get rusty in my career.

Maria03-26-25 - AB, Canada

I found Jenn's videos near the end of my discrete math class, so I only had a month to go through all of her discrete math lessons to study for my exam. I'm sure I would have aced it if I had more time but I got a pretty good grade considering I thought I would fail.So happy to be done that class!As advertised, Jenn is very thorough and doesn't skip steps, she lets you know exactly how she gets from a to b or she will refer you to other videos where she teaches the techniques she's using more in depth. This was extremely valuable to me, being a mature student taking advanced math while not remembering basic algebra.And it was fun to understand and solve complex problems vs memorize proof structures.

Robbin03-18-25 - CO, United States

Very well organized, helpful and comprehensive. It is great also to have access to prior course material so you can easily go back and refresh if you need to. Jenn is very clear and the number of examples leaves one comfortable with each topic. Couldn't be happier.

RCJK03-07-25 - ID, United States

I had to take Calculus I and II as accelerated classes while working full time. It was my first time taking this courses and was very overwhelming. Calcworkshop really made learning the subjects easier for me by having all the subjects easy to find and easy to understand explanations. I received a B in both classes which I am extremely happy with doing the classes in double time.

Jacqueline S.03-07-25 - SC, United States

Jenn is awesome!Her breakdown of the topic is beyond what you would expect. She is showing you how to arrive at the answer instead of doing a simple equation. Most people need to know the why it give confidence and structure to the learning process. This is what Jenn is great at, she knows how to deliver the information to a non math mind in a way that instills knowledge that you can forever draw from as you move forward. It's really well thought out. She is a true master teacher. Thanks for all that you do for us! Hugs n Blessings... JS

Jujuana03-05-25 - MO, United States

I love the videos the way each lesson is explained step by step. I love that she has examples that you can go over again and again in order to understand the way algebra works. I was lost because my instructor was flying through each lesson and I was totally lost. I attached my syllabus and they helped me stay focus on what I was working and give me a guide to go back and refresh what I went over in class.

Stacey01-31-25 - AZ, United States

Hello, I highly recommend getting a subscription to Jenn and her Calcworkshop teaching math service. I did a general, "go from bad to good at math", Google search and found out about Calcworkshop through responses to the topic on reddit. I've just started watching her videos and found them to be extremely helpful. I'm going back to college after a long absence and math was never my strong suit. So I'm starting at the very bottom of her available subjects and going from there. Just watching a couple of the videos has taken me from being dragged along not understanding to following along just fine in my math class. I'm moving from the "I'll never get this", to the "I look forward to understanding this", mindset in approaching math. This for me is huge, and even though I have a long way to go, I'm confident I will get there thanks to Jenn. Totally worth it!

Kathy W.01-14-25 - WA, United States

Calcworkshop is an outstanding source to learn math and understanding math concepts. Jenn is an outstanding master teacher. Every lesson is clearly presented making understanding easy to grasp. Practice lessons with accompanying answers are given for each section. I am 82, a retired teacher and lifelong learner. Learning calculus has always been on my bucket list. Calcworkshop is helping me reach my goal.

Cheryl01-14-25 - NY, United States

Calc workshop is the absolutely best resource for math and I have seen almost everything that exists out there. I have even recommended it to my daughter's school so that all the kids could use the videos during the summer months for the subject they plan to study in the fall. They are guaranteed to get a A if they have watched the videos and completed the problems before taking the class. Students who are weak in areas can access lower level classes and those who seek to advance above grade level can do so. The videos and exercises are crystal clear and the excellent presentations raise the bar for teachers everywhere. I have always believed that one great math teacher is important in the education process. The videos, exercises and problems are excellent. It is not possible to have ANY knowledge gaps. I have never seen anything on the market that even begins to compete with it!

Justin N.12-22-24 - OK, United States

Calculus can be a scary subject. I know I was scared. I had been out of any math class for over 23 years. I had taken an 8 week Calculus 1 class and felt like I was overloaded. Going into Calculus 2 I found CALCWORKSHOP.com. I used the training videos and material to really dive back into Calc 1 and prepare for Calc 2. Long story short with the material provided and ample study time, I finished Calc 2 with a 95%. Thanks Jenn!

Shelby12-10-24 - OH, United States

CalcWorkshop was a wonderful resource as someone going onto a college calculus 1 class after not having taken a math course in a year! Jenn always explained things in a logical order that built upon previous lessons, and the way she explained topics was always easy to understand. Calcworkshop saved this semester for me, and I couldn't be more grateful to have found this site. :)

Jordan Q.12-09-24 - AR, United States

Anyone struggling with math at any level would greatly benefit from this product. I signed up for it immediately after getting a D on my first exam in calculus 2 and ended up getting A's and B's on the remaining exams, getting a B overall in the class. Jenn breaks down the topics, without skipping any steps, in a way that makes them very easy to understand. I highly recommend this product!

N8Booker11-28-24 - MA, United States

I'm in school to get my degree Networking and Cybersecurity and I'm in my first year. I've been away from school for quite a long time so the concepts that are being taught although not foreign to me, have so much dust on them from a lack of being used in real world applications regularly.I stumbled upon CalcWorkshop by pure chance and it has been a game changer for me. Jen filled in the gaps in between what my Professor is teaching at a rapid fire pace and where my brain grasps and applies it. If not for Jen's approach, I'd have failed my test I took miserably!Am I grateful? It goes beyond words and not I recommend her workshops to everyone!

Gina K.03-30-25 - WA, United States

Maria03-26-25 - AB, Canada

RCJK03-07-25 - ID, United States

See more reviews on Shopper Approved