In today’s geometry lesson, you’re going to learn about similar polygons.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
We’re going to take a step-by-step approach to setup, identify, and use our detective skills once again to find missing side lengths and other unknown measures.
So let’s get started!
What Are Similar Polygons?
To define similar polygons we need to start with the concept of congruent polygons.
As you may recall, congruent polygons have the exact same size and are a perfect match because all corresponding parts are congruent (equal). Whereas, similar polygons have the same shape, but not the same size (i.e., one is bigger than the other).
This means that if two polygons are similar, then their corresponding angles are congruent but their their corresponding sides are proportional as displayed in the figure below.
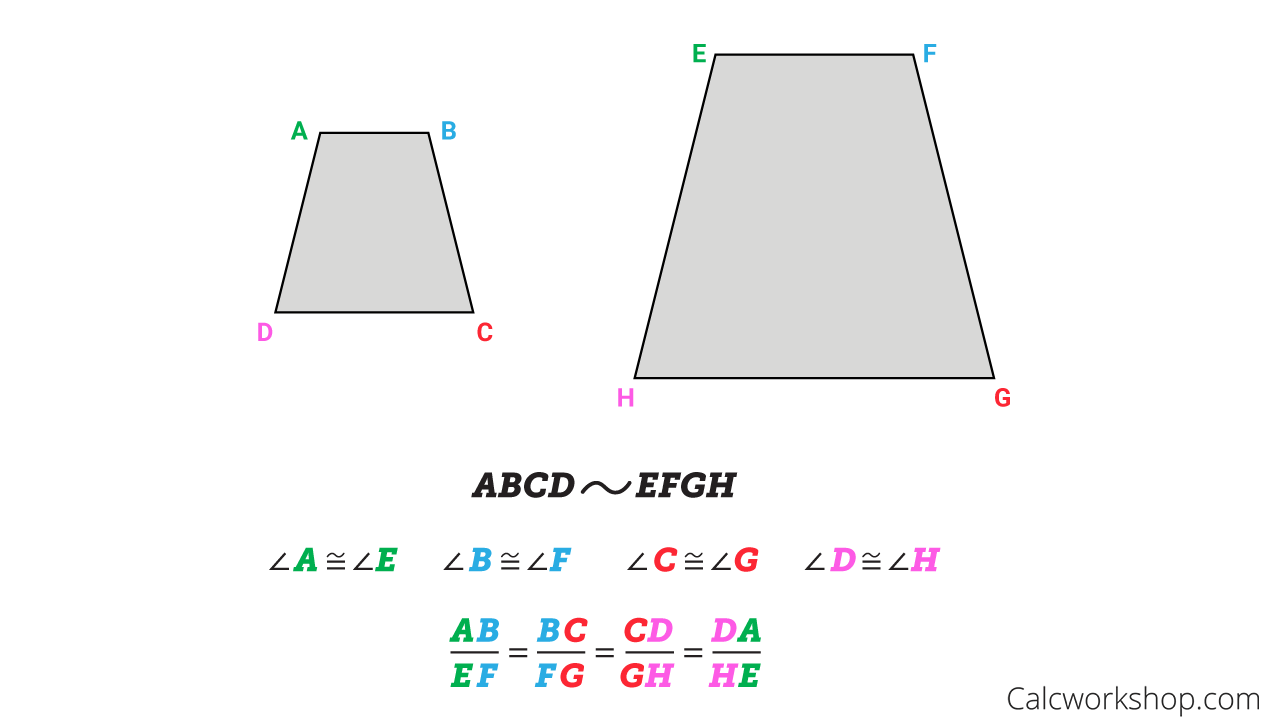
Similar and Congruent Figures
Remember, a ratio is a fraction comparing two quantities, and a proportion is when we set two ratios equal to each other. And we can use cross multiplication to solve a proportion.
Checkout the video below for a review of ratios and proportions.
Scale Factor
So how do we create a proportion?
We need a scale factor!
If two polygons are similar, then the ratio of the lengths of any two corresponding sides is called the scale factor. This means that the ratio of all parts of a polygon is the same as the ratio of the sides.
For example, using the figure above, the simplified ratio of the lengths of the corresponding sides of the similar trapezoids is the scale factor.
And as ck-12 accurately states, if two polygons are similar then not only are their side lengths proportional, but their perimeters, areas, diagonals, medians, midsegments, and altitudes are proportional too.
And why are scale factors important?
Because if we have a scale factor then we can find all missing side lengths as well!
How To Find Scale Factor?
To find the scale factor, we simply create a ratio of the lengths of two corresponding sides of two polygons. If the ratio is the same for all corresponding sides, then this is called the scale factor and the polygons are similar.
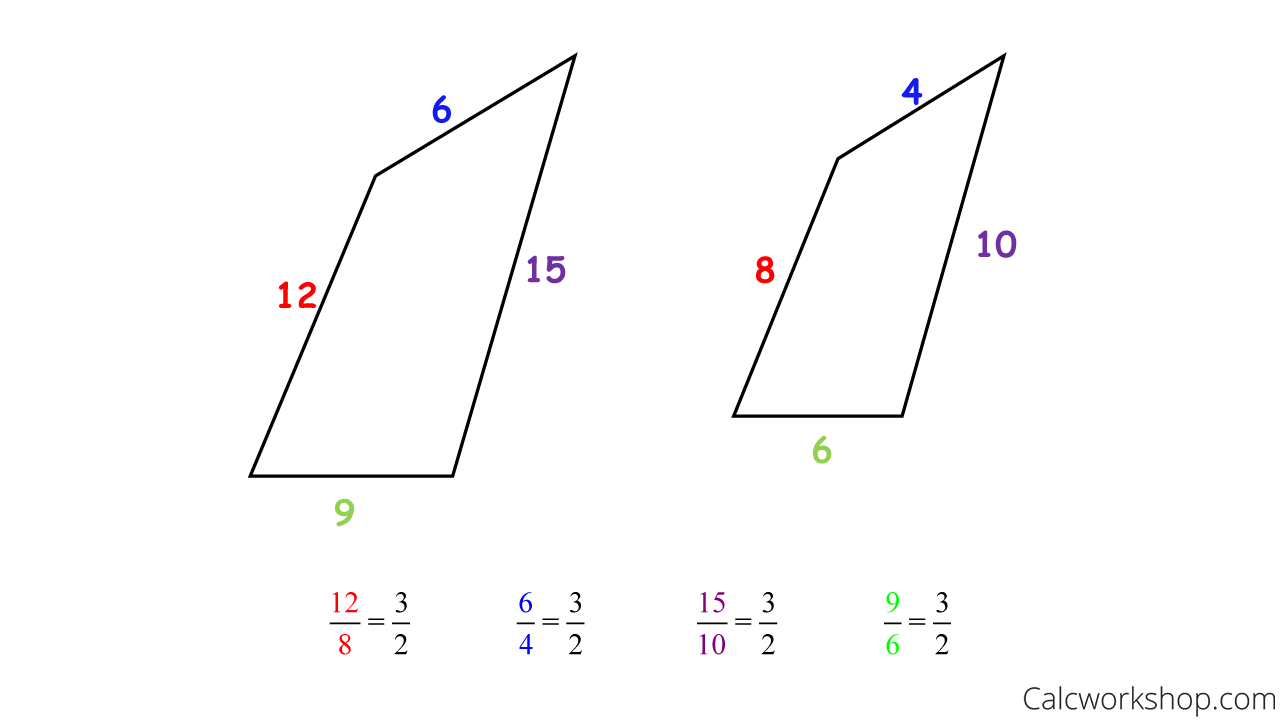
Scale Factor Example
The above example indicates that the scale factor for the two quadrilaterals is 3/2 and proves that the two polygons are indeed similar.
In the video below we are going to review how to solve proportions, determine if two polygons are similar by creating scale factors, and learn how to solve for unknown measures.
Similar Polygons – Lesson & Examples (Video)
1 hr 4 min
- Introduction
- 00:00:33 – Overview of the topic including properties of proportions
- 00:06:09 – Solve each proportion (Examples #1-3)
- 00:13:11 – Write the ratio as a fraction in simplest form (Examples #4-7)
- Exclusive Content for Member’s Only
- 00:16:32 – Determine whether the proportion is true or false (Examples #8-13)
- 00:25:38 – Using the diagram and given proportion find the unknown length (Examples #14)
- 00:28:16 – Using the diagram and given proportion find the unknown length (Examples #15-16)
- 00:34:07 – Overview of scale factor
- 00:36:50 – Determine if the polygons are similar. If yes, find the scale factor (Examples #17-22)
- 00:50:57 – Find the indicated measures for the given problems (Examples #23-24)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.