Set operations and their properties

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
As we previously learned, a set is the unordered collection of distinct elements. But what do we do when we want to combine two or more sets to produce another set?
We need set operations!
The most common operations with sets are:
- Union
- Intersection
- Difference
- Complement
Let’s take a closer look at each of these operations.
Union
Definition
The union of sets A and B is the set of elements that are in A or B or both A and B. In other words, it is the smallest set that contains all the elements of both sets.
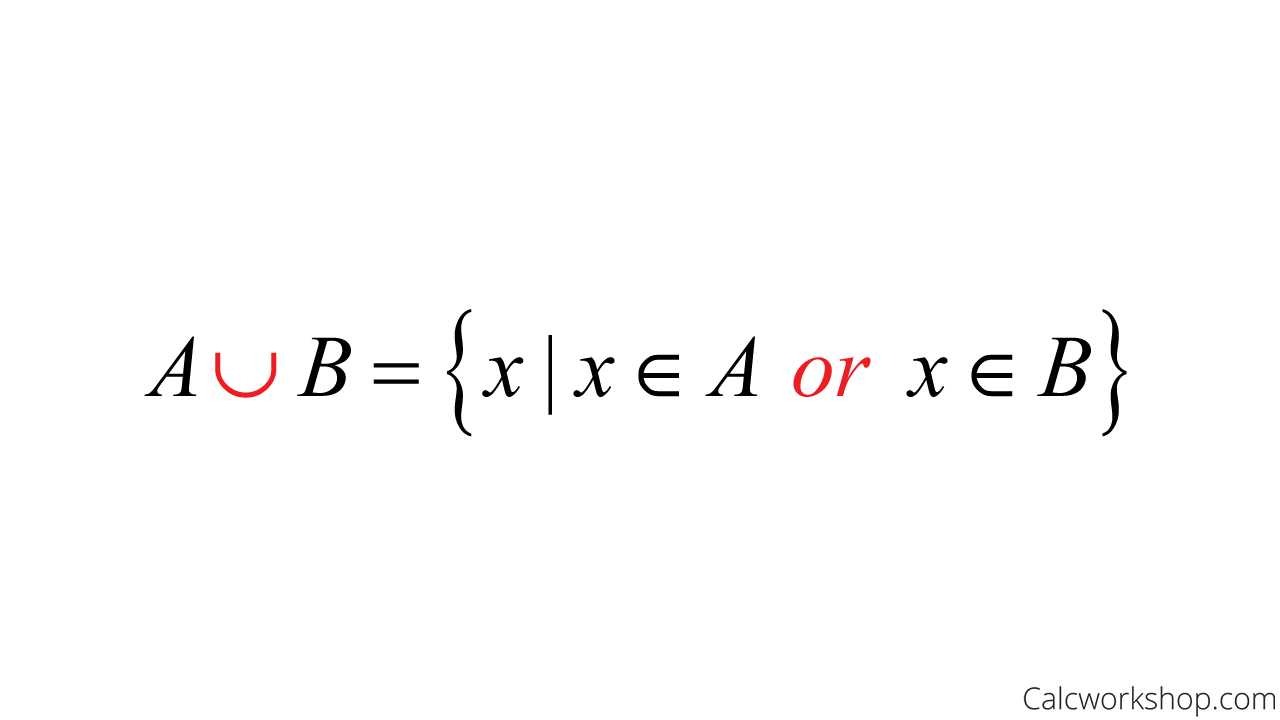
Union Symbol
Example
For instance, suppose:
- set A = {apple, orange, banana, pear}
- set B = {strawberry, apple, lemon, orange, peach}
The union of set A and B is the list of elements that are in A or B or both A and B:

Union Of Sets
Notice that the union list each element only once, even if it appears in both sets.
Intersection
Definition
The intersection of sets A and B is the set of elements A and B have in common. In other words, it is the largest set that contains all of their shared elements.
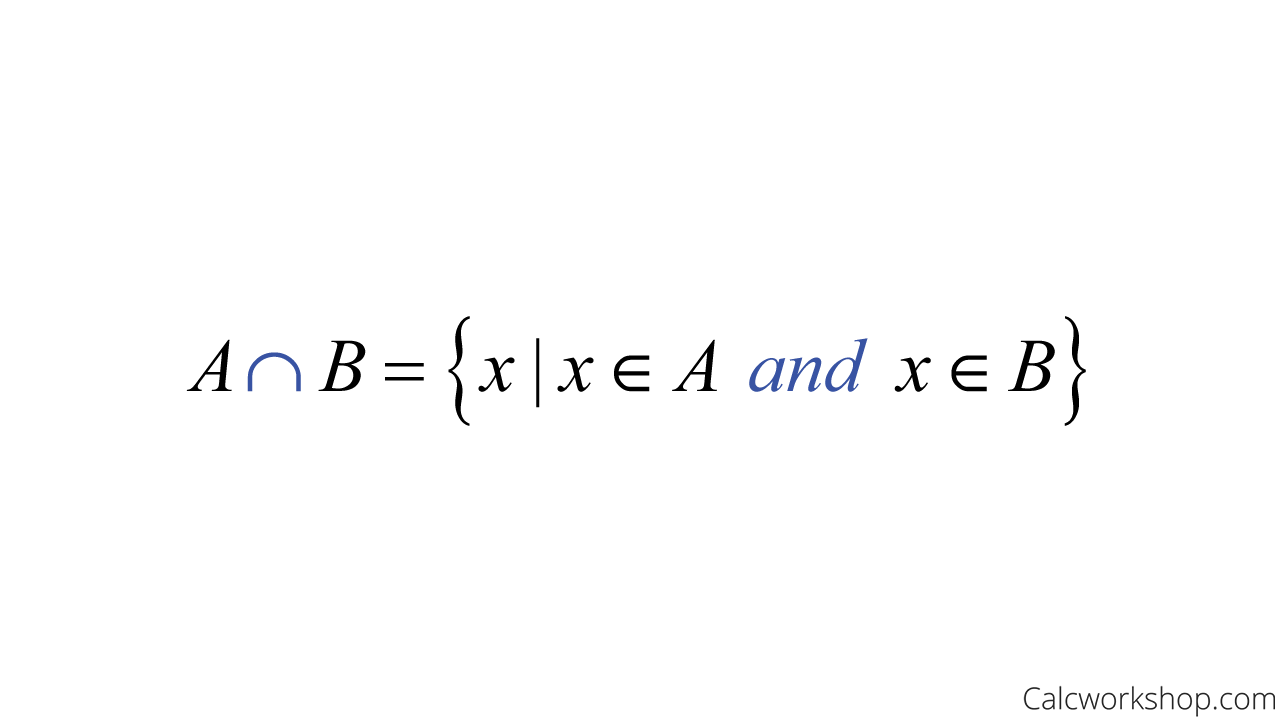
Intersection Symbol
Example
Using our problem from above, suppose:
- set A = {apple, orange, banana, pear}
- set B = {strawberry, apple, lemon, orange, peach}
The intersection of set A and B is the list of elements that are shared in A and B:
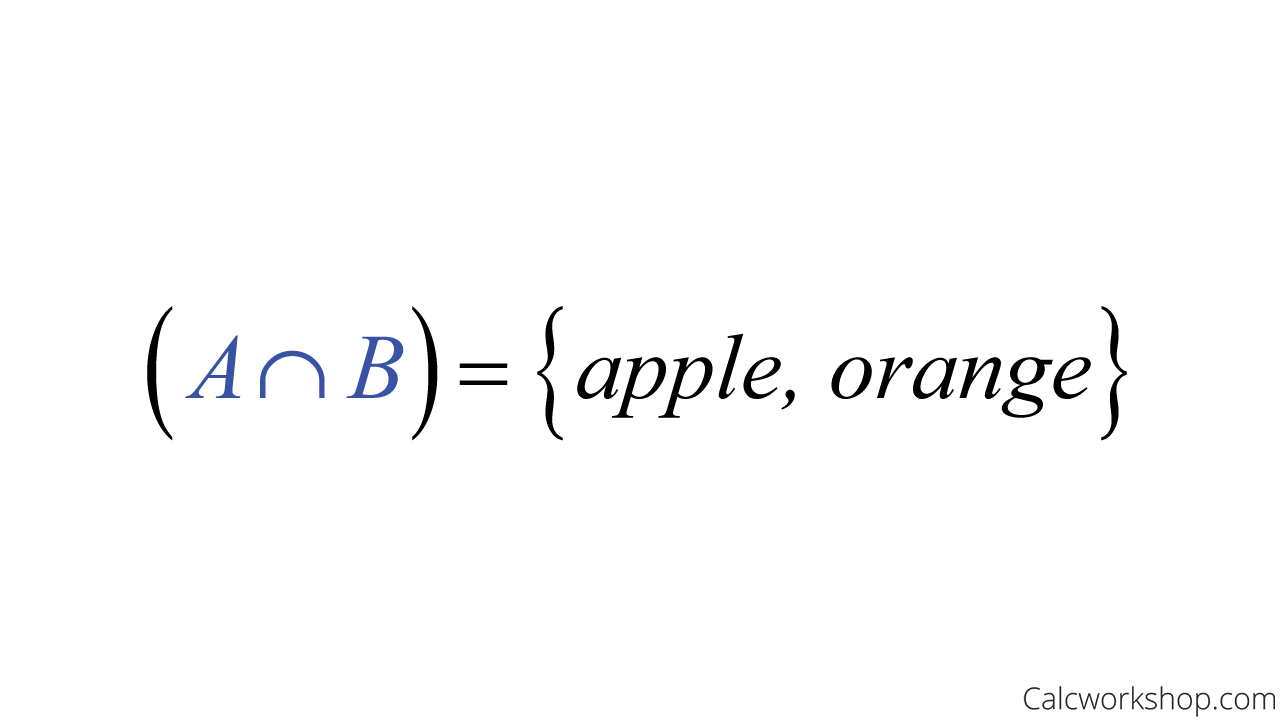
Intersection Of Sets
But what happens if two sets don’t have anything in common?
When two sets have no common elements, this is called mutual exclusion or simply disjoint. In other words, the intersection of two disjoint sets is the empty set.

Disjoint Symbol
Example
Let’s imagine you have these sets:
- set A = {apple, orange, banana, pear}
- set B = {strawberry, lemon, peach}
Since there are no shared elements between sets A and B, their intersection is the empty set — thus, declaring set A and set B to be disjoint.
And a collection of three or more sets is pairwise disjoint if any two sets in the collection are disjoint.
Example
In this problem you’re given these 3 sets.
- set A = {apple, orange}
- set B = {banana, pear}
- set C = {strawberry, lemon, peach}
Since there are no shared elements between sets A , B or C they are pairwise disjoint.
Complement
Definition
Now, the complement of A is the set of all elements in the universal set, not in set A.
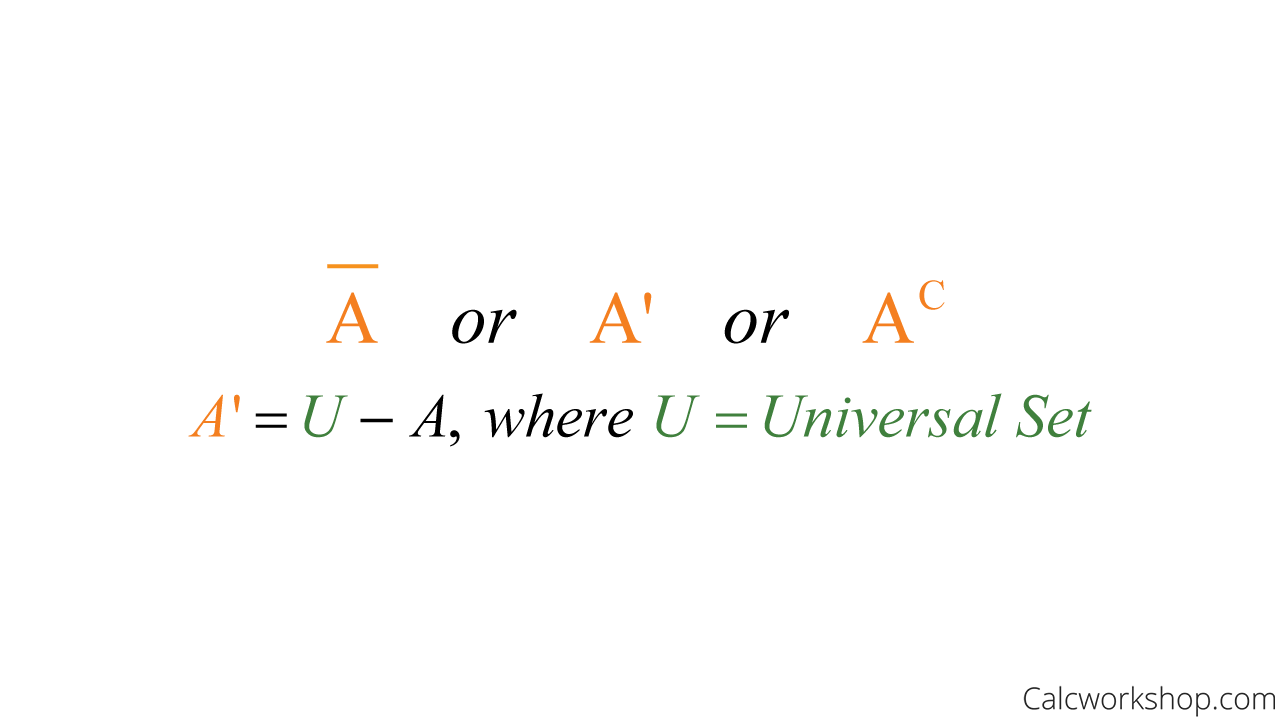
Complement Symbol
Example
Let’s assume you’re given the 2 sets below:
- Universal set = {apple, orange, banana, pear, strawberry, lemon, peach}
- set A = {orange, pear, strawberry, peach}
Then the complement of set A would be {apple, banana, lemon}
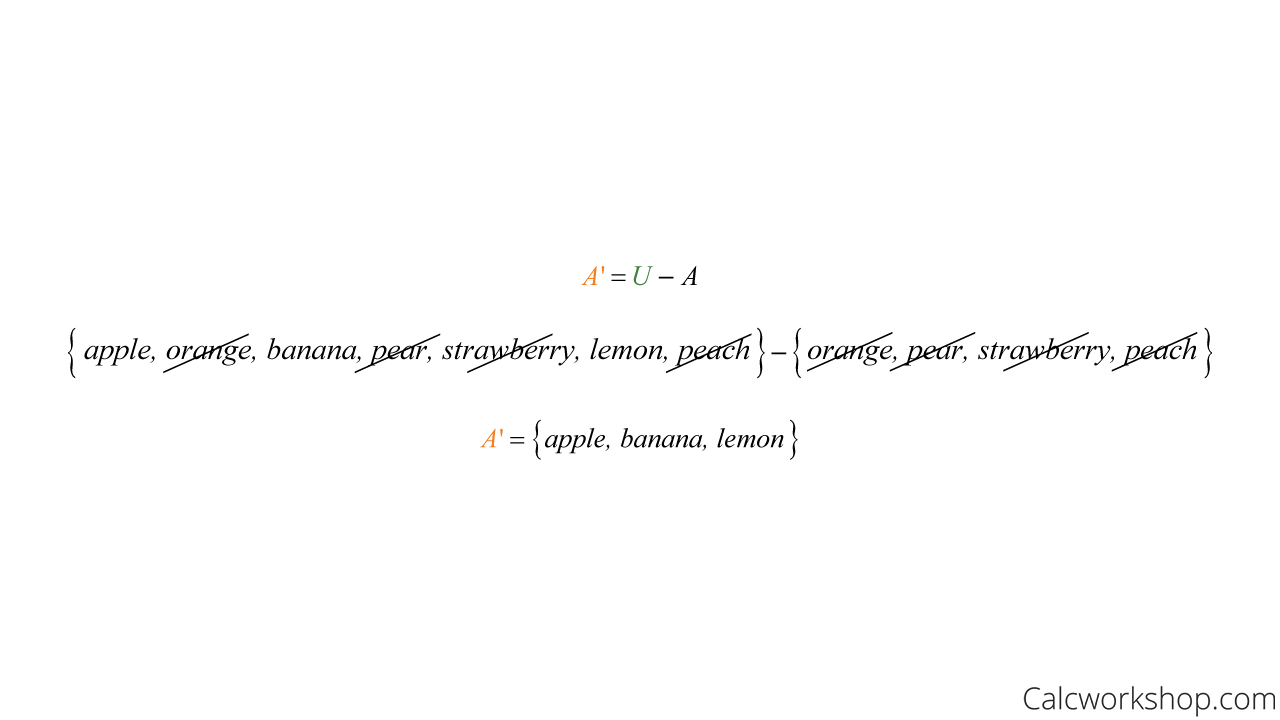
Complement Of A Set
Notice, all we did was cross out everything in U that was also in set A, and whatever was left in set U is in the complement of A.
Difference
Definition
And this brings us to the idea of the difference of sets. This is exactly as it sounds. We want to find the difference between two sets (i.e., subtract one from the other). The difference between set A and B, denoted A–B or A\B, is the set containing those in A but not in B.
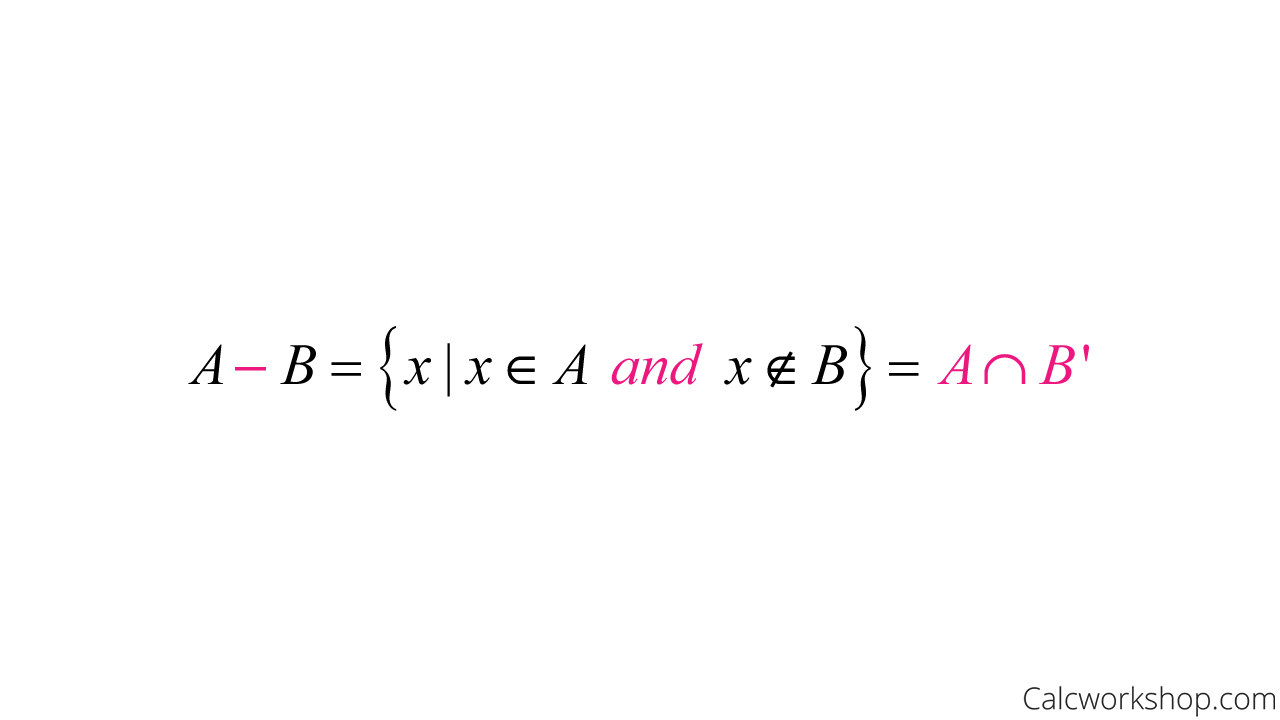
Set Difference Symbol
Example
In this question, suppose we wish to find A-B and also B-A of the following sets.
- set A = {apple, orange, banana, pear}
- set B = {strawberry, orange, banana, lemon}
Then all we have to do is subtract those elements from our first set that also appears in our second set.

Set Difference
Compliment Vs Set Difference
Please do not confuse the complement with a difference. The complement is the difference of the universal set with set A, whereas the difference of sets is the difference between A and B, not the universal set.
In addition, the University of Pittsburgh has a set operations PDF that provides some additional material to reinforce your knowledge.
Inclusion Exclusion Principle
Finally, this brings us to the Principle of Inclusion-Exclusion (PIE), which is an extremely important technique used in enumeration, counting, and probability.
The basic premise of PIE is that it computes the number of elements (cardinality) in the union of two or more sets and prevents double counting.
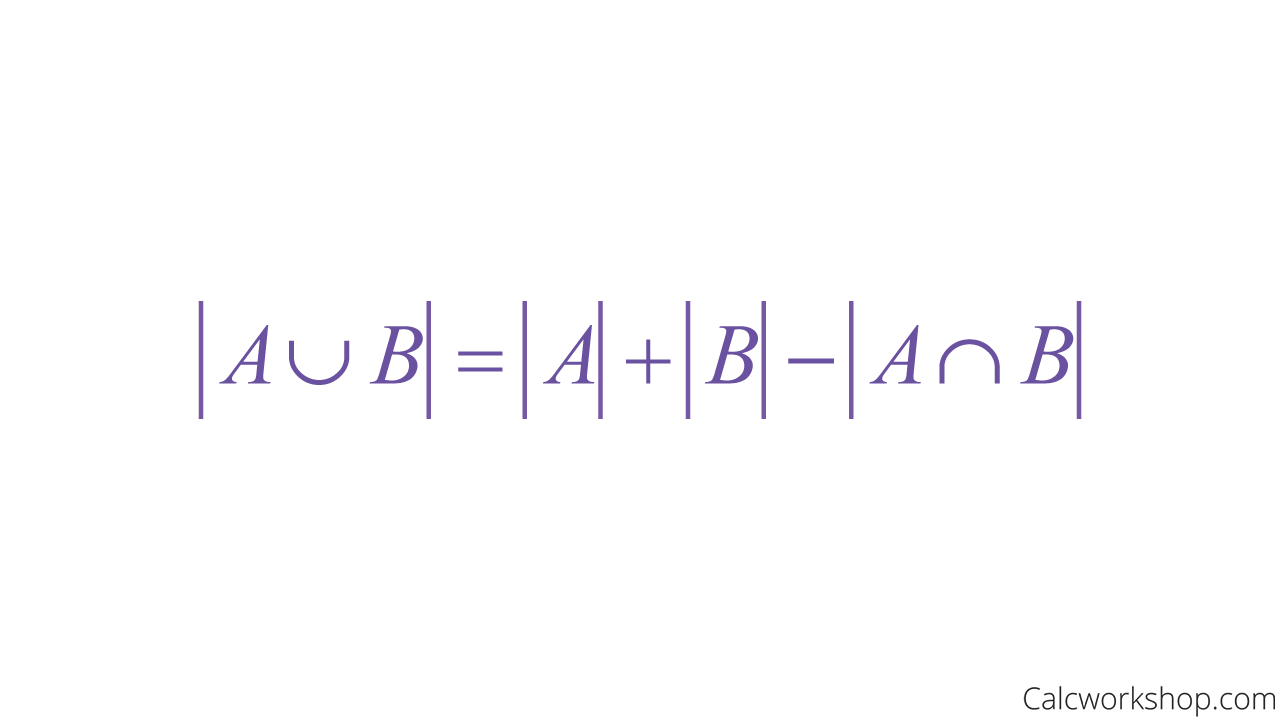
Inclusion Exclusion — Formula
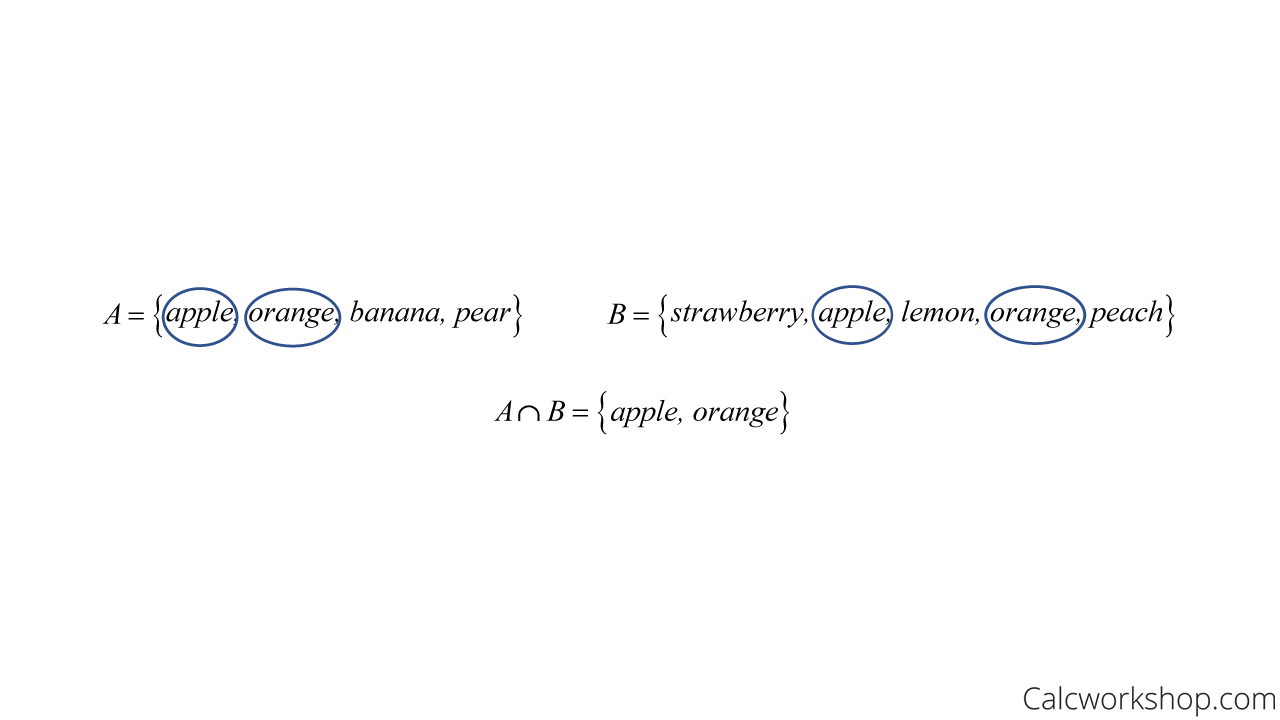
For example, using our example for the union of sets, we let:
- set A = {apple, orange, banana, pear}
- set B = {strawberry, apple, lemon, orange, peach}
First, we will find the intersection of sets A and B, which is {apple, orange}.
Intersection — Example
Next, we find the cardinality of set A, set B, and the intersecting set and get 4, 5, and 2, respectively.
Now, using the principle of inclusion-exclusion, we find that the number of elements in the union of sets A and B to be 4 + 5 – 2 = 7.
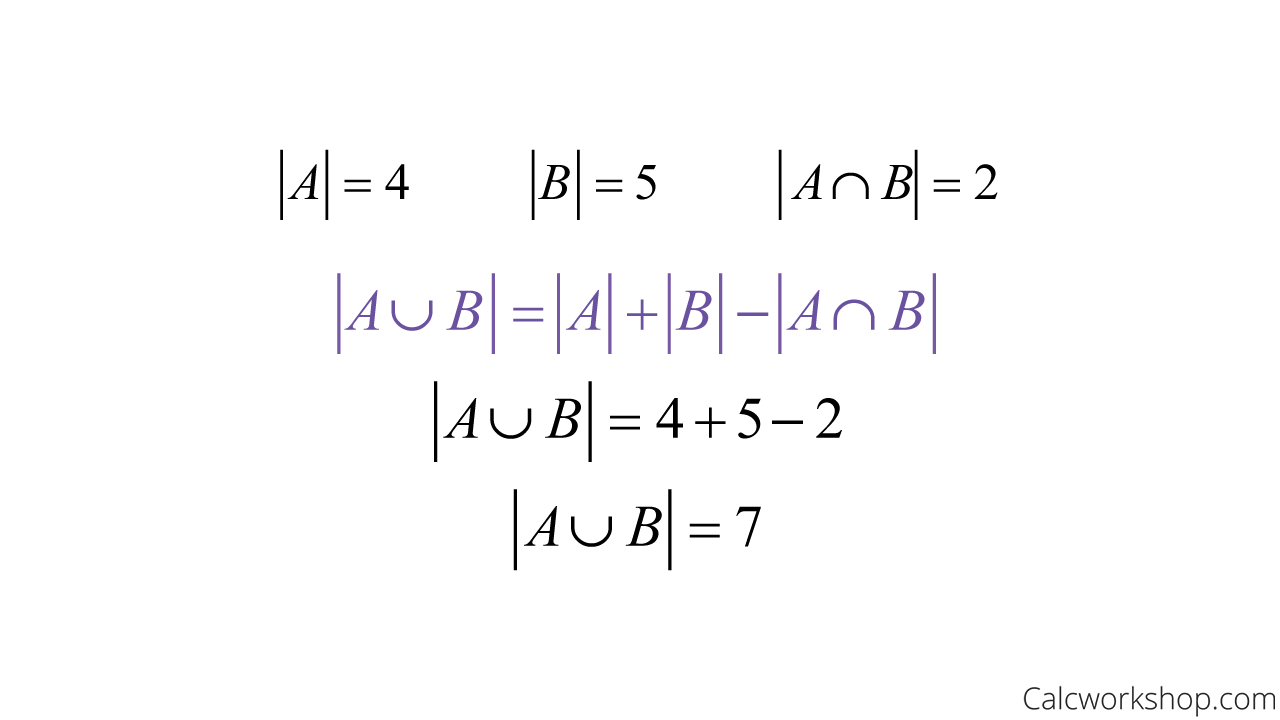
Inclusion Exclusion Principle — Example
Which we can verify as being true, seeing as the union of sets A and B is {apple, orange, banana, pear, strawberry, lemon, peach}, which does indeed have seven elements!
Symmetric Difference
And lastly, we need to look at the symmetric difference of sets A and B. This is a set of elements belonging to A or B, but not both.

Symmetric Difference Notation
Example
So now, let’s test your knowledge with these sets.
- set A = {apple, orange, banana, pear}
- set B = {strawberry, apple, lemon, orange, peach}
Then the symmetric difference of sets A and B is {strawberry, banana, pear, peach}.
Together in this lesson, we will use our good friend, Venn Diagrams, to help us graphically represent sets and perform operations on sets with ease.
Bit String
Moreover, we will learn how to find a computer representation of sets.
A bit string is a sequence of bits, where a bit is a digit that is either 0 or 1 and is used for storing elements and representing data.
So, let’s look at how we change a set into a bit array.
Suppose we let our universal set U = {apple, orange, banana, pear, strawberry, lemon, peach}, and using bitwise operation, we wish to find the yellow fruit.
Here’s how.
The only yellow fruits in the set are the banana and lemon. Therefore they will be represented with a 1 (true), and every other element in the set will be represented by a 0 (false).
Thus, the bit-string would be {0, 0, 1, 0, 0,1, 0}.
Set Partition
And another way we can represent a set is through partitioning.
The partition of a set is a collection of nonempty subsets such that every element of the set belongs to precisely one of the subsets.
In other words, the union of all the subsets equals the original set, the intersection of any two subsets is empty, and none of the partitions is the empty set.
For example, suppose set A = {apple, orange, banana, pear, strawberry, lemon, peach} then two possible partitions would be

Partition Example
Notice how each subset is pairwise disjoint!
Minterm
Lastly, we will discuss a minset, sometimes referred to as the minimum set or minterm, which helps us partition a set efficiently into a minimum number of pairwise disjoint sets.
For example, suppose
- set A = {apple, orange, banana, pear}
- set B = {lemon, orange, banana, pear, strawberry}
- set C = {apple, pear, peach}
First, let’s put this into a Venn Diagram.

Minterm Example
Notice the natural partitions that the Venn Diagram illustrates. But what’s even more exciting is that the Venn Diagram helps us to find the minsets quite quickly, as the minimum number of disjoint sets are each partitioned group!
{ {apple} , {peach} , {pear}, {orange, banana} , {lemon, strawberry} }
Together we will learn set notation and vocabulary as we perform set operations, including bit strings and partitions.
It’s going to be fun!
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 34 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.