In our previous lesson, Taylor Series, we learned how to create a Taylor Polynomial (Taylor Series) using our center, which in turn, helps us to generate our radius and interval of convergence, derivatives, and factorials.
We also learned that there are five basic Taylor/Maclaurin Expansion formulas. We discovered how we can quickly use these formulas to generate new, more complicated Taylor Polynomials easily. Additionally, we learned
- How to take derivatives of these Taylor Polynomials
- Find specific terms and/or coefficients
- How to integrate and evaluate a Taylor Series
But in all Taylor or Maclarin Series, there will always be some form of error involved simply because we are not generating a polynomial that has an infinite number of terms.
So how do we account for this error?
How do we find it?
Well, in this lesson we will learn that there are three different types of Error:
- Actual Error
- Error for an Alternating Series
- Lagrange Error Bound (i.e., Taylor’s Remainder Theorem)
In essence, this lesson will allow us to see how well our Taylor Polynomials approximates a function, and hopefully we can ensure that the error is minimal (small).
What is most important to understand is that error is defined to be the absolute value of the difference between the actual value and the approximation.
Sometimes, this is easy to calculate, and other times it is downright challenging.
Consequently, there are times when we will have to be satisfied with finding the worst case scenario: Lagrange Error Bound. The Lagrange Error Bound formula gives us an interval of how great the error will be, without pinpointing it exactly.
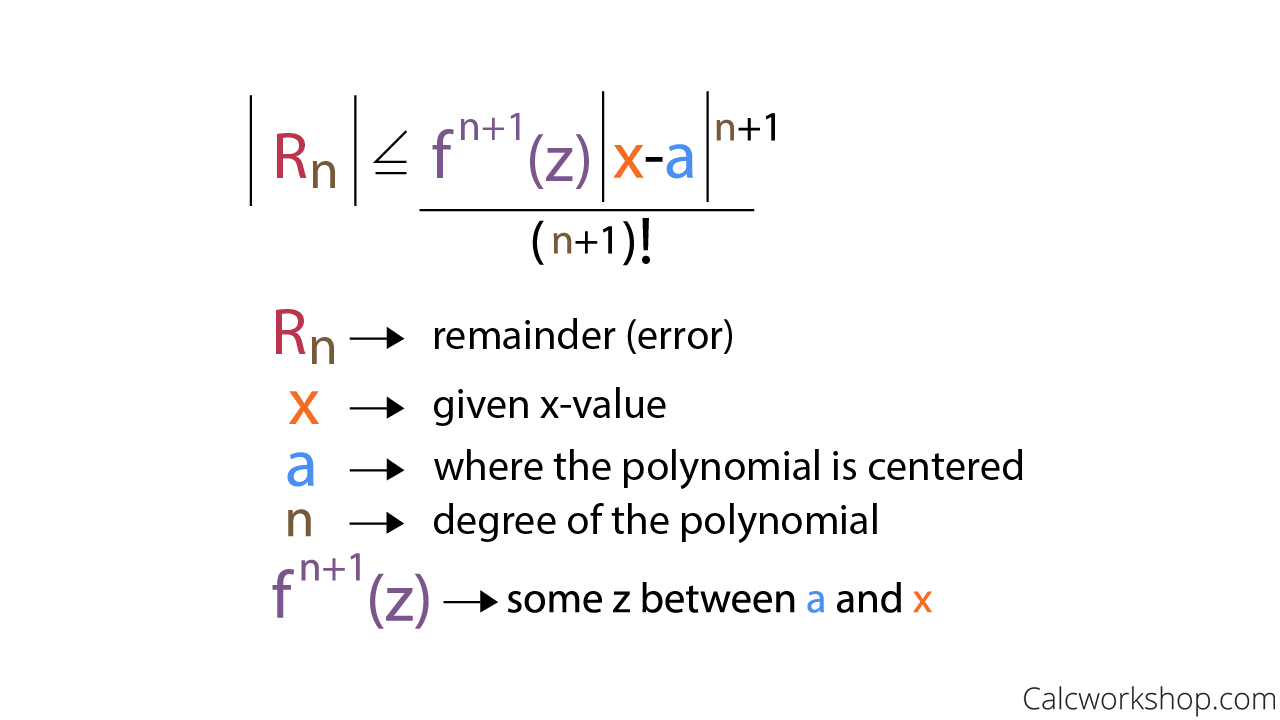
Lagrange Error Bound Formula
In it’s current state, this formula doesn’t yield itself to easy use. Thankfully, by rewriting the formula to make it easier to understand, we can clearly see that we are merely looking for the maximum value in the interval as you can see with this new and improved Lagrange Error Bound Formula.
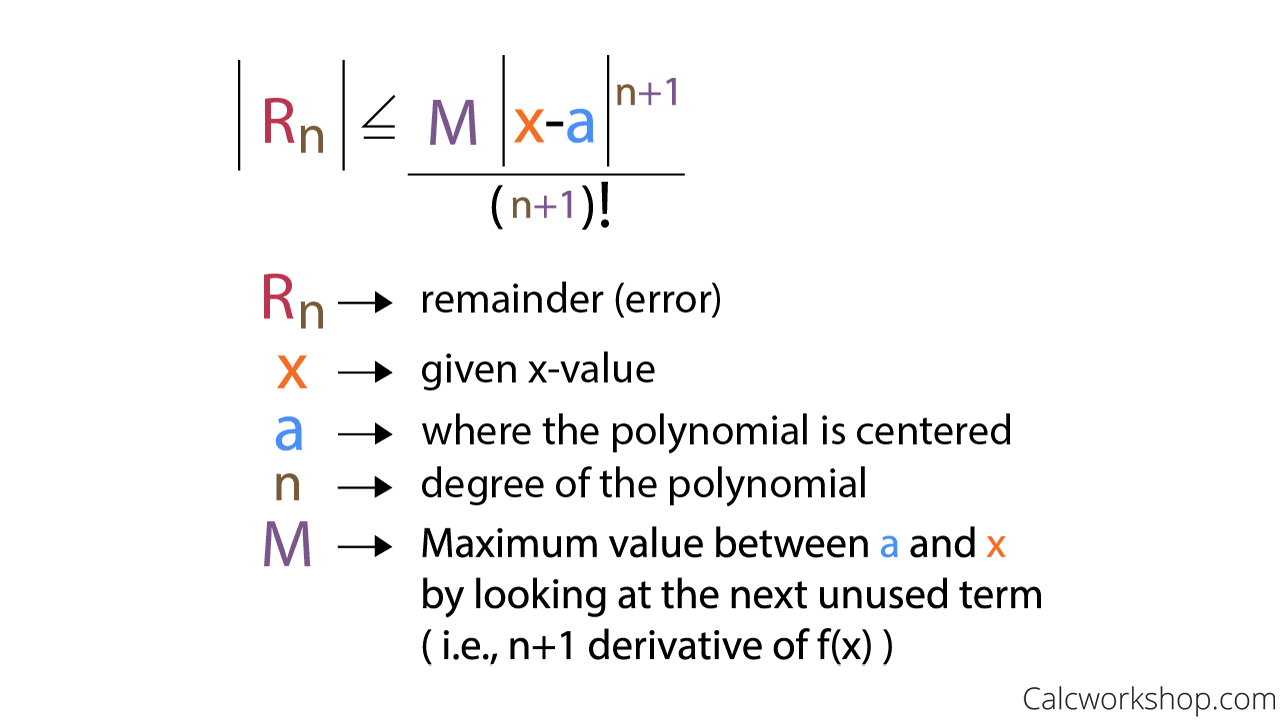
Improved Error Bound Formula
By the end of this lesson you will be convinced that the Lagrange Error is extremely effective and straightforward to find. Moreover, as Lin McMullin discusses, we will soon see that using either the Alternating Series Error or the Lagrange Error Bound formula will give us a handle on the size of our error when we create Taylor Polynomials.
Lagrange Error Bound – Video
Lagrange Error Bound Examples
Lagrange Error Bound Overview with Examples in Calculus
- What is True/Actual Error?
- Error for an Alternating Series Overview
- Example 1 for Alternating Error
- Example 2 for Alternating Error
- Example 3 for Alternating Error
- Overview of Taylor’s Remainder Theorem and Lagrange Error Bound
- Example 1 for finding Lagrange Error
- Example 2 for finding Lagrange Error
- Example 3 for finding Lagrange Error
- Example 4 for finding Lagrange Error
- Example 5 for finding Lagrange Error
- Overview of Example using all of our Series and Error Techniques
- Part A of Example – Finding a Taylor Polynomial
- Part B of Example – Integrating our Taylor Polynomial
- Part C of Example – Finding the Radius and Interval of Convergence for our Taylor Series
- Part D of Example – Finding Error for our Taylor Polynomial using Alternating Error and Lagrange Error Bound
Get more examples and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.