Just as we saw in our previous lesson, P Series Test, there are tests that play an important role in determine convergence of an infinite series.
The Geometric Series Test is one the most fundamental series tests that we will learn.
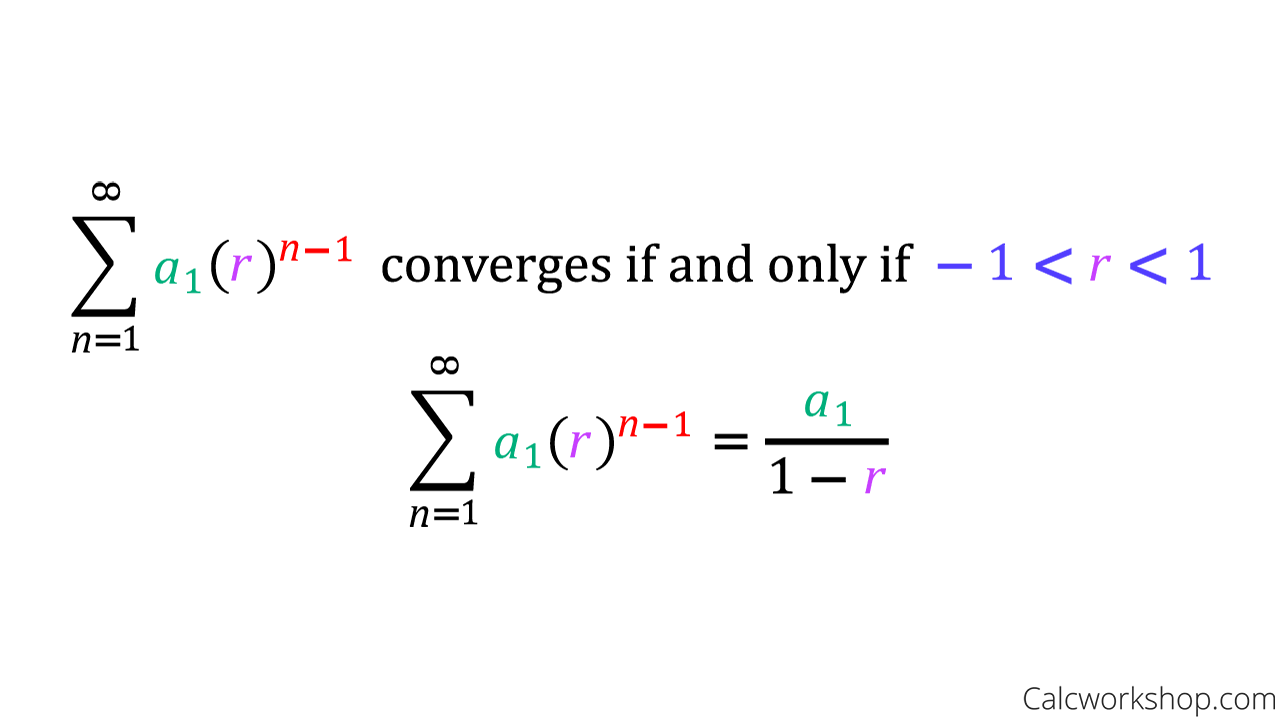
Determining Convergence of an Infinite Geometric Series
While the p-series test asks us to find a variable raised to a number, the Geometric Series test is it’s counterpart.
We are looking for a number raised to a variable!
And not just any number, but a fraction called the common ratio, r, and for the series to converge its value must be between negative one and positive one.
Additionally, the geometric series has another incredible feature! While some tests are able to indicate whether a series converges or not, the geometric series test goes above and beyond and provides us with what the series converges to.
Even, Paul’s Online Notes calls the geometric series a special series because it has two important features:
- Allows us to determine convergence or divergence,
- Enables us to find the sum of a convergent geometric series
Moreover, this test is vital for mastering the Power Series, which is a form of a Taylor Series which we will learn in future lessons.
Geometric Series Video
Geometric Series Example
Geometric Series Overview with Example in Calculus
- Geometric Series Test Overview
- Example 1
- Example 2
- Example 3
- Example 4
Get 3 more examples and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.