Ready to learn a series test that is super easy to spot and also easy to apply?
Look no further than the The Alternating Series Test.
The reason why it is so easy to identify is that this series will always contain a negative one to the n, causing this series to have terms that alternate in sign.
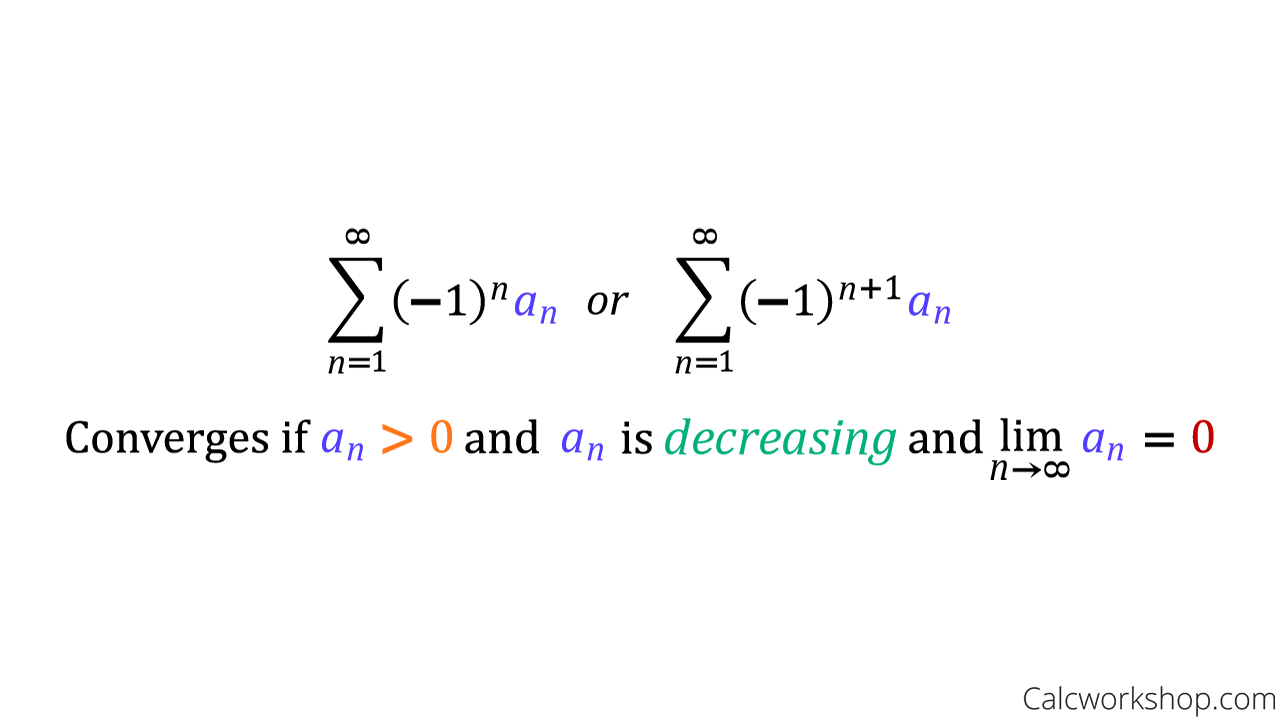
Properties of the Alternating Series Test
By definition, an alternating series is one whose terms alternate positive and negative, and our goal is to determine whether these alternating terms are decreasing toward zero in absolute value.
So what does this mean?
Well, if we apply the absolute value to the alternating series, then the alternating part (i.e, the negative one to the nth power) goes away allowing us to focus on the remaining function.
Then we determine that the partial sums are decreasing, and lastly we apply an infinite limit to the series to determine convergence, as Wikipedia accurately states.
Together we will look at how wonderful the alternating series test is, and how effortless it is to use. And we will also learn how an alternating series may have Conditional or Absolute Convergence.
Additionally, our skills learned in this lesson will help us to determine the radius and interval of convergence of a power series as well as finding error in approximating sums.
Alternating Series Test Video
Alternating Series Test Examples
Alternating Series Test Overview with Examples in Calculus
- Alternating Series Test Overview
- Example 1
- Example 2
- Example 3
- Conditional and Absolute Convergence for Alternating Series
- Example 1
- Example 2
Get more examples and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.