Solving DEs with Distinct Real Roots (Step-by-Step)

Solving second order and higher order differential equations can be challenging, but for homogeneous, constant coefficient differential equations, we can use an easy-to-follow process that transforms our differential equation into a straightforward polynomial equation.

Jenn (B.S., M.Ed.) of Calcworkshop® teaching distinct real roots

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

How?

By the principal of superposition and the characteristic equation!

In fact, solving a second-order DE for distinct real roots has never been easier.

Let’s take a look.

Formulating the General Solution for Homogeneous Differential Equations

Okay, so a second-order differential equation is said to be linear if it can be written as

$\begin{array}{r} a_{2} y^{''} + a_{1} y^{'} + a_{0} y = f (x) \end{array}$

We call the function $f (x)$ on the right a forcing function since, in physical applications, it’s often related to a force acting on some system modeled by the differential equation. And if $f (x) = 0$ then DE is homogeneous, and nonhomogeneous if $f (x) \neq 0$

Now, if each coefficient $a_{2}, a_{1}, a_{0}$ is a constant and $f (x) = 0$ , then obtaining a solution to the differential equation is really quite simple because all we have to do is assume a possible solution.

First, let us guess that a possible solution of the equation $a_{2} y^{''} + a_{1} y^{'} + a_{0} y = 0$ is $y = e^{r x}$ . Next, we must ask ourselves, “For what values of $r$ will yield a solution?”

Well, we know that a value must be for which

$a_{2} \frac{d^{2}}{d x^{2}} e^{r x} + a_{1} \frac{d}{d x} e^{r x} + a_{0} e^{r x} = 0$

$a_{2} r^{2} e^{r x} + a_{1} r e^{r x} + a_{0} e^{r x} = 0$

And if we divide by $e^{r x}$ we obtain an algebraic equation, called the characteristic equation, in terms of $r$

$a_{2} r^{2} + a_{1} r + a_{0} = 0$

So, if we solve the characteristic equation above, we will find the value of $r$ for which $y = e^{r x}$ is a solution.

Wow!

Now, the characteristic equation, sometimes called the auxiliary equation, is easily obtained by replacing $y$ by $r$ and the order of the derivative by a numerically equal exponent.

In fact, this process can be extended to homogeneous linear higher order differential equations of the form $a_{n} y^{(n)} + a_{n - 1} y^{(n - 1)} + \dots + a_{2} y^{''} + a_{1} y^{'} + a_{0} y = 0$ , where the coefficients $a_{i}$ are real constants.

Three Possible Solutions to the Characteristic Equation

It is also important to note that when solving the characteristic equation, there are three possible solutions:

All roots are real and distinct
All roots are real, but some repeat
All roots are imaginary or complex

Steps for Solving Homogeneous Differential Equations with Constant Coefficients

And the steps for solving for the general solution to a second-order or higher-order homogeneous differential equation with constant coefficients are straightforward:

Step 1: Write the characteristic equation
Step 2: Solve the polynomial equation for factors by using factoring, quadratic formula, synthetic division, etc.
Step 3: Substitute each root into the general form:

$y = c_{1} e^{r_{1} t} + c_{2} e^{r_{2} t} + \dots + c_{n} e^{r_{n} t}$

Focus on Real and Distinct Roots

Please note that this lesson will focus on the roots of the characteristic equation that are real and distinct (different). In subsequent lessons, we will explore other possibilities, such as repeated roots and complex roots.

The main difference when dealing with complex roots lies in the characteristic equation, which requires a different general solution form involving trigonometric functions, sine and cosine, instead of exponential functions used for real and distinct roots.

Example: Solving a Second-Order Differential Equation

Let’s look at an example to see this process in action.

Find the general solution $y (t)$ of $y^{''} - 3 y^{'} + 2 y = 0$

First, we will transform our DE into the characteristic equation.

$a_{2} r^{2} + a_{1} r + a_{0} = 0$

$y^{''} - 3 y^{'} + 2 y = 0$

$r^{2} - 3 r + 2 = 0$

Next, we will solve the quadratic polynomial for our roots.

$\begin{array}{r} \begin{aligned} r^{2} - 3 r + 2 = 0 \\ (r - 2) (r - 1) = 0 \\ r_{1} = 2, r_{2} = 1 \end{aligned} \end{array}$

Now we plug our roots into the general solution formula of

$\begin{aligned} y = c_{1} e^{r_{1} t} + c_{2} e^{r_{2} t} + \dots + c_{n} e^{r_{n} t} \\ y = c_{1} e^{2 t} + c_{2} e^{1 t} \end{aligned}$

Easy, right! Okay, let’s look at a higher-order DE and apply the same process.

Example: Solving a Higher-Order Differential Equation

Find the general solution $y (t)$ of $y^{(4)} - y^{'''} - 4 y^{''} + 4 y^{'} = 0$

First, we will transform our DE into the characteristic equation.

$\begin{array}{r} \begin{aligned} y^{(4)} - y^{'''} - 4 y^{''} + 4 y^{'} = 0 \\ r^{4} - r^{3} - 4 r^{2} + 4 r = 0 \end{aligned} \end{array}$

Next, we will solve the quadratic polynomial for our roots.

$\begin{array}{r} \begin{aligned} r^{4} - r^{3} - 4 r^{2} + 4 r = 0 \\ r (r^{3} - r^{2} - 4 r + 4) = 0 \\ r (r - 1) (r^{2} - 4) = 0 \\ r (r - 1) (r - 2) (r + 2) = 0 \\ r_{1} = 0, r_{2} = 1, r_{3} = 2, r_{4} = - 1 \end{aligned} \end{array}$

Now we plug our roots into the general solution formula.

$\begin{array}{r} \begin{aligned} y = c_{1} e^{r_{1} t} + c_{2} e^{r_{2} t} + \dots + c_{n} e^{r_{n} t} \\ y = c_{1} e^{0 t} + c_{2} e^{1 t} + c_{3} e^{2 t} + c_{4} e^{- 2 t} \\ y = c_{1} + c_{2} e^{t} + c_{3} e^{2 t} + c_{4} e^{- 2 t} \end{aligned} \end{array}$

And that’s all there is to it! Nice!

Next Steps

Up next, you’ll:

Deepen your understanding of second-order linear differential equations, a crucial skill in mathematics and engineering.
Master the steps to find the general solution, enabling you to solve various types of differential equations.
Improve your problem-solving skills by learning how to avoid common mistakes and tackle complex problems confidently.
Expand your knowledge of real and complex roots, providing a comprehensive understanding of roots in differential equations.
Enhance your ability to work with initial conditions, an essential skill for solving real-world problems involving differential equations.

It’s going to be fun, so let’s jump right in!

Video Tutorial w/ Full Lesson & Detailed Examples

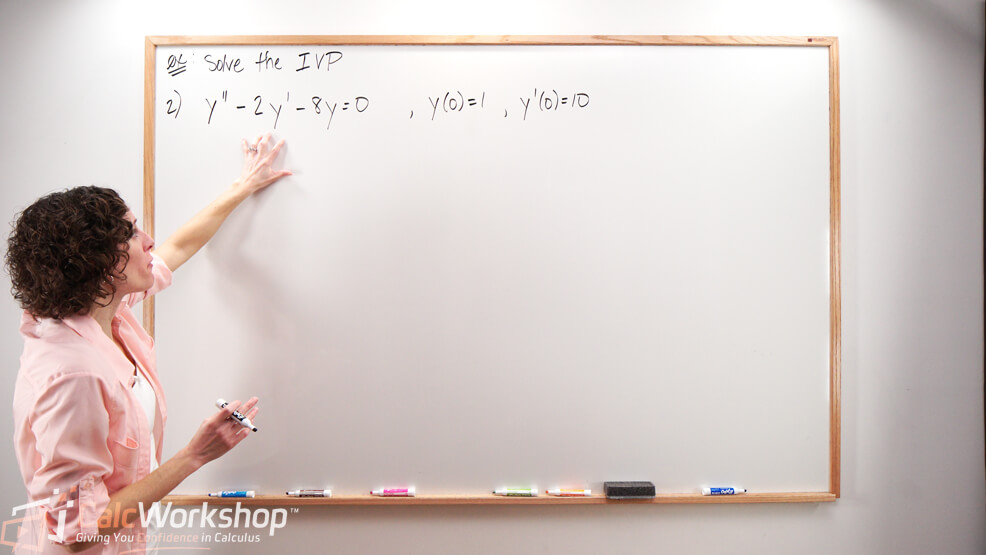
distinct real roots example

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.

4.9 / 5

1,138 Reviews

N8Booker11-28-24 - MA, United States

I'm in school to get my degree Networking and Cybersecurity and I'm in my first year. I've been away from school for quite a long time so the concepts that are being taught although not foreign to me, have so much dust on them from a lack of being used in real world applications regularly.I stumbled upon CalcWorkshop by pure chance and it has been a game changer for me. Jen filled in the gaps in between what my Professor is teaching at a rapid fire pace and where my brain grasps and applies it. If not for Jen's approach, I'd have failed my test I took miserably!Am I grateful? It goes beyond words and not I recommend her workshops to everyone!

Patrick04-09-25 - NJ, United States

I went through the discrete math course prior to taking it at a university. Jen made difficult concepts easy to understand, leaving me well prepared for my Discrete college course.

Enzo D.04-08-25 - Italy

I highly recommend Calcworkshop - a 'gradus ad Parnassum' that opens the door to the wonders of pure and applied math to all, and a model of how math should be taught!

Jon, C.04-06-25 - MD, United States

CalcWorkshop is a premier resource for any student seeking to understand, practice, and succeed within the vast areas of mathematics. I am impressed with the quality of instruction and practice problems offered by Jenn. As a engineering student, I always utilize Calcworkshop as a the "first stop" to really understand and gain confidence in the subject. I credit my success in Calculus to Jenn and CalcWorkshop and making me "smarter than the average bear."

Sayida S.04-03-25 - PA, United States

I absolutely love this subscription. At first I was iffy about spending the money, but in the long term it is so worth it. I started watching Jenn almost 3/4ths into my calc 2 class, and I a confidently say I understand the depths to each topic. Before, with my professor I felt that I only understood surface level of each topic. But after the CalcWorkshop videos, I have acronyms, tips, and knowledge I walk away with, that I didn't have before. Genuinely cannot wait to keep using this website for my future endeavors, minoring in Mathematics!

Addie M.04-01-25 - United States

The best resource for improving my math skills and improving my performance in Calculus, as well as through other areas that pertain to other math courses! Jenn is an incredible teacher and I recommend Calcworkshop to anyone who experiences insecurity in math.

Gina K.03-30-25 - WA, United States

My experience was great! I needed help studying for my math class, but I wasn't sure how-until an ad for this popped up on my YouTube. After watching the ad, I was convinced, so I subscribed to CalcWoskop. I'm so happy I did because it helped me so much with my class! I learned a lot that I couldn't grasp from my college lectures, and this was the perfect solution.

Maria03-26-25 - AB, Canada

I found Jenn's videos near the end of my discrete math class, so I only had a month to go through all of her discrete math lessons to study for my exam. I'm sure I would have aced it if I had more time but I got a pretty good grade considering I thought I would fail.So happy to be done that class!As advertised, Jenn is very thorough and doesn't skip steps, she lets you know exactly how she gets from a to b or she will refer you to other videos where she teaches the techniques she's using more in depth. This was extremely valuable to me, being a mature student taking advanced math while not remembering basic algebra.And it was fun to understand and solve complex problems vs memorize proof structures.

RCJK03-07-25 - ID, United States

I had to take Calculus I and II as accelerated classes while working full time. It was my first time taking this courses and was very overwhelming. Calcworkshop really made learning the subjects easier for me by having all the subjects easy to find and easy to understand explanations. I received a B in both classes which I am extremely happy with doing the classes in double time.

Jacqueline S.03-07-25 - SC, United States

Jenn is awesome!Her breakdown of the topic is beyond what you would expect. She is showing you how to arrive at the answer instead of doing a simple equation. Most people need to know the why it give confidence and structure to the learning process. This is what Jenn is great at, she knows how to deliver the information to a non math mind in a way that instills knowledge that you can forever draw from as you move forward. It's really well thought out. She is a true master teacher. Thanks for all that you do for us! Hugs n Blessings... JS

Jujuana03-05-25 - MO, United States

I love the videos the way each lesson is explained step by step. I love that she has examples that you can go over again and again in order to understand the way algebra works. I was lost because my instructor was flying through each lesson and I was totally lost. I attached my syllabus and they helped me stay focus on what I was working and give me a guide to go back and refresh what I went over in class.

Stacey01-31-25 - AZ, United States

Hello, I highly recommend getting a subscription to Jenn and her Calcworkshop teaching math service. I did a general, "go from bad to good at math", Google search and found out about Calcworkshop through responses to the topic on reddit. I've just started watching her videos and found them to be extremely helpful. I'm going back to college after a long absence and math was never my strong suit. So I'm starting at the very bottom of her available subjects and going from there. Just watching a couple of the videos has taken me from being dragged along not understanding to following along just fine in my math class. I'm moving from the "I'll never get this", to the "I look forward to understanding this", mindset in approaching math. This for me is huge, and even though I have a long way to go, I'm confident I will get there thanks to Jenn. Totally worth it!

Kathy W.01-14-25 - WA, United States

Calcworkshop is an outstanding source to learn math and understanding math concepts. Jenn is an outstanding master teacher. Every lesson is clearly presented making understanding easy to grasp. Practice lessons with accompanying answers are given for each section. I am 82, a retired teacher and lifelong learner. Learning calculus has always been on my bucket list. Calcworkshop is helping me reach my goal.

Cheryl01-14-25 - NY, United States

Calc workshop is the absolutely best resource for math and I have seen almost everything that exists out there. I have even recommended it to my daughter's school so that all the kids could use the videos during the summer months for the subject they plan to study in the fall. They are guaranteed to get a A if they have watched the videos and completed the problems before taking the class. Students who are weak in areas can access lower level classes and those who seek to advance above grade level can do so. The videos and exercises are crystal clear and the excellent presentations raise the bar for teachers everywhere. I have always believed that one great math teacher is important in the education process. The videos, exercises and problems are excellent. It is not possible to have ANY knowledge gaps. I have never seen anything on the market that even begins to compete with it!

Justin N.12-22-24 - OK, United States

Calculus can be a scary subject. I know I was scared. I had been out of any math class for over 23 years. I had taken an 8 week Calculus 1 class and felt like I was overloaded. Going into Calculus 2 I found CALCWORKSHOP.com. I used the training videos and material to really dive back into Calc 1 and prepare for Calc 2. Long story short with the material provided and ample study time, I finished Calc 2 with a 95%. Thanks Jenn!

Shelby12-10-24 - OH, United States

CalcWorkshop was a wonderful resource as someone going onto a college calculus 1 class after not having taken a math course in a year! Jenn always explained things in a logical order that built upon previous lessons, and the way she explained topics was always easy to understand. Calcworkshop saved this semester for me, and I couldn't be more grateful to have found this site. :)

Jordan Q.12-09-24 - AR, United States

Anyone struggling with math at any level would greatly benefit from this product. I signed up for it immediately after getting a D on my first exam in calculus 2 and ended up getting A's and B's on the remaining exams, getting a B overall in the class. Jenn breaks down the topics, without skipping any steps, in a way that makes them very easy to understand. I highly recommend this product!

N8Booker11-28-24 - MA, United States

Jon, C.04-06-25 - MD, United States

Sayida S.04-03-25 - PA, United States

See more reviews on Shopper Approved