There is a special class of second-order differential equations with non-constant coefficients in which we can employ an ingenious method for finding the general solution.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It is called the Cauchy-Euler Equation.
What makes Cauchy-Euler equations so special?
Well, they are a type of differential equation with variable coefficients where the monomial coefficients match the order of differentiation.
Characteristics of Cauchy-Euler Equations
In fact, the Cauchy-Euler Equation, or simply the Euler Equation, is a linear homogeneous ordinary differential equation sometimes referred to as an equidimensional equation because it is a simple structure where the exponents and derivatives match!
Let’s take a look.
\begin{align*}
a_{n} x^{n} \frac{d^{n} y}{d x^{n}}+a_{n-1} x^{n-1} \frac{d^{n-1} y}{d x^{n-1}}+\cdots+a_{1} x \frac{d y}{d x}+a_{0} y=g(x)
\end{align*}
So, if the exponent on the variable matches the order of differentiation, then it’s a Cauchy-Euler equation, and we can use a really neat technique to solve for the homogeneous solution and variation of parameters to find the particular solution.
Solving Cauchy-Euler Equations: General Steps
What is the method of solution for the Cauchy-Euler equation?
1. Transform the Cauchy-Euler second-order DE of the form
\begin{equation}
a x^2 \frac{d^2 y}{d x^2}+b x \frac{d y}{d x}+c y=0
\end{equation}
into its characteristic (auxiliary) equation using the following formula
\begin{align*}
a m^{2}+(b-a) m+c=0
\end{align*}
2. Solve the quadratic for real and distinct roots, real and repeating roots, or complex roots to find the complementary (homogeneous) solution
Real and Distinct Roots: \(y=c_{1} x^{m_{1}}+c_{2} x^{m_{2}}\)
Real and Repeating Roots: \(y=c_{1} x^{m_{1}}+c_{2} x^{m_{1}} \ln x\)
Complex Roots: \(y=x^{\alpha}\left[c_{1} \cos (\beta \ln x)+c_{2} \sin (\beta \ln x)\right]\) where \(m=\alpha \pm \beta i\)
3. If the \(\mathrm{DE}\) is nonhomogeneous, then proceed with variation of parameters to find the particular solution.
4. Write the general solution for the DE knowing \(y=y_{h}+y_{p}\)
Visualizing Cauchy-Euler Equation Solutions
To better understand the different types of solutions for Cauchy-Euler equations, let’s visualize each case with the help of plots:
Real and Distinct Roots
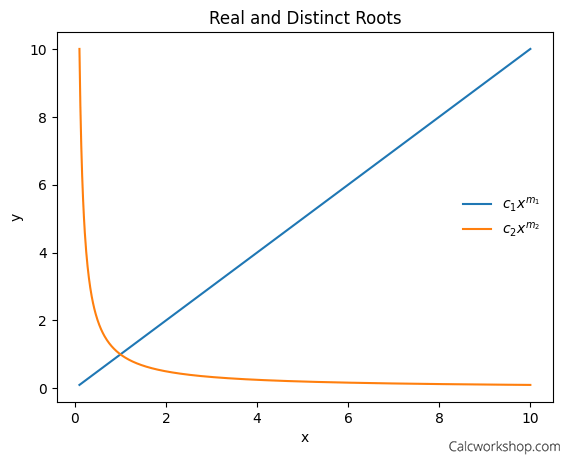
Visualizing solutions of a Cauchy-Euler equation with real and distinct roots: two distinct power functions with varying exponents.
This plot shows the two distinct power functions for the case of real and distinct roots. The exponents m1 and m2 influence the shape of the functions, illustrating how the solutions change with different exponents.
Real and Repeating Roots
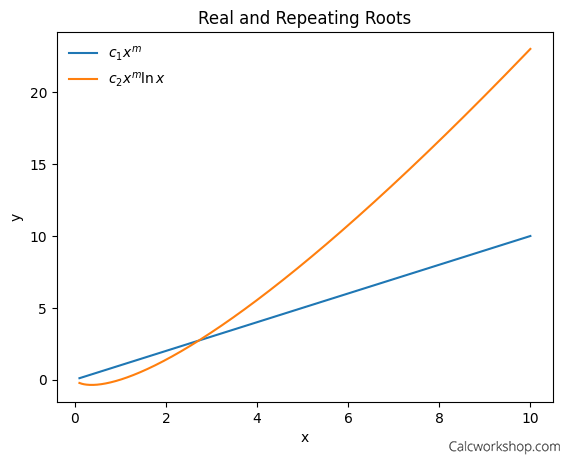
Visualizing solutions of a Cauchy-Euler equation with real and distinct roots: two distinct power functions with varying exponents.
In this plot, we can observe the effect of the logarithmic term for the case of real and repeating roots. The second function demonstrates a distinct behavior compared to the first power function due to the presence of the logarithmic term.
Complex Roots
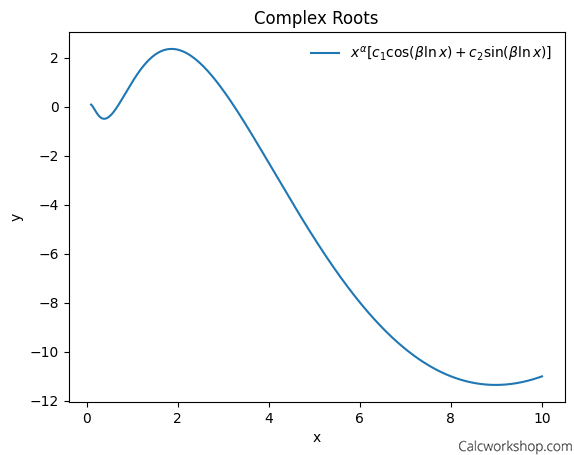
Oscillatory solution curve for a Cauchy-Euler equation with complex roots: a function combining cosine and sine terms with varying amplitudes.
The plot for complex roots highlights the oscillatory behavior of the solution, which results from the combined effect of the exponential, cosine, and sine components. This visualization helps to convey the unique nature of the complex roots case.
Example: Solving a Cauchy-Euler Equation
Let’s look at an example to see these fantastic equations in action. Solve \(2 x^{2} y^{\prime \prime}+3 x y^{\prime}-y=0\)
First, we notice that we have variable coefficients and that exponents on the variables match the order of differentiation, so this is an Euler equation. Additionally, we are given a homogeneous DE, so we only need to solve for the complementary solution.
So, we will transform our DE into its characteristic equation using the Cauchy-Euler formula.
If \(2 x^{2} y^{\prime \prime}+3 x y^{\prime}-y=0\) where \(a=2, b=3\), and \(c=-1\) the
\begin{align*}
\begin{aligned}
& a m^{2}+(b-a) m+c=0 \\
& 2 m^{2}+(3-2) m+(-1)=0 \\
& 2 m^{2}+m-1=0
\end{aligned}
\end{align*}
Now we need to solve our characteristic equation for its roots.
\begin{align*}
\begin{aligned}
& 2 m^{2}+m-1=0 \\
& (2 m-1)(m+1)=0 \\
& m_{1}=\frac{1}{2} \text { and } m_{2}=-1
\end{aligned}
\end{align*}
Because we found two distinct, real roots, we will use the following formula to find our general solution.
\begin{align*}
\begin{aligned}
& y=c_{1} x^{m_{1}}+c_{2} x^{m_{2}} \\
& y=c_{1} x^{1 / 2}+c_{2} x^{-1}
\end{aligned}
\end{align*}
And that’s it!
Easy, right?
Next Steps
You’ll…
- Deepen your understanding of Cauchy-Euler equations as you explore creating characteristic equations and writing general solutions for various root types.
- Enhance problem-solving skills by following along with the video, covering real and distinct roots, real roots with multiplicity, and complex conjugate roots.
- Identify and classify different types of Cauchy-Euler equations easily by learning the unique characteristics of each root type.
Let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.