What is partial order?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Imagine you’re cooking a large dinner for family and friends. Your guests will be arriving in three hours, and you need to prepare a tantalizing appetizer, a savory main course, two tasty side dishes, and a decadent dessert. What do you do?
Knowing that you have limited time and cooking space, you develop a plan on how to complete each task and which order these tasks should be done because some dishes must be cooked before others while some tasks can be achieved simultaneously.
This is the idea of partial ordering.
Partial Order — Defined
A binary relation R on a set S is called a partial ordering, or partial order if and only if it is:
- Reflexive
- Antisymmetric
- Transitive
As noted by Mount Royal University.
Poset
It is essential to mention that the symbol used for partial ordering looks like the inequality “less than.” It is merely a symbol representing any relation — thus, we could denote a poset at (S, R) where R is some relation.

Partial Order Symbol
Partial Order Relations
Now, the three fundamental partial order relations are:
- Less Than Or Equal To
- Subset
- Divisibility
For example, let’s show that “divisibility” is a partial order relation on A.

Partial Order Proof — Divisibility
And did you know that the reason why a partial ordering has the name that it does is because pairs for elements or tasks can be either comparable or incomparable. Consequently, some pairs of of elements or tasks must come before another (comparable) or they do not need to come before but can be performed simultaneously or separately (incomparable).
For example, these are the following tasks that Sparky, a discrete mathematics student, does every morning upon waking up: shower, breakfast, put on pants, shirt, socks, shoes, watch, and jacket, and is highlighted in the Hasse Diagram below.
What is so important to note is that Sparky can put on pants, socks, or shirt in any order, as it doesn’t matter if Sparky puts on a shirt before putting on pants. But other tasks must be done in order, as it wouldn’t make sense to put shoes on before socks. This is the idea behind partial ordering, where tasks that are “ordered” are considered comparable and those tasks that are “unordered” are called incomparable.
This is an example of topological sorting, and helps project managers with scheduling applications, and is a real-life application of partial ordering.
Partial Order Vs Total Order
Comparability means that the elements a and b of a poset (S, ≼) are comparable if either a ≼ b or b ≼ a. In other words, task a must come before b or task b must come before a.
If (S, ≼) is a poset and every two elements of S are comparable, then S is called a totally ordered set, sometimes called a linearly ordered set or chain.
For example, the set of integers over the relation “less than or equal to” is a totally ordered set because for every element a and b in the set of integers, either a ≼ b or b ≼ a, thus showing order.
And (S, ≼) is a well-ordered set if it is a poset such that ≼ is a total ordering and every nonempty subset of S has a least element.
For example, the set of natural numbers over the relation “less than or equal to” is well-ordered because for every element a and b in the set of natural numbers, either a ≼ b or b ≼ a, thus showing a totally ordered set.
Additionally, I want you to notice that this total ordering has a “least element,” namely the value of 1, as this is the smallest (least) natural number in the chain.
Hasse Diagram
The best way to graphically understand and represent partial orders is via a Hasse Diagram.
A Hasse diagram is a graph for a partial ordering that does not have loops or arcs that imply transitivity and is drawn upward, thus, eliminating the need for directional arrows.
How To Draw A Hasse Diagram
To construct a Hasse diagram, we follow these four steps:
Step 1
Create a directed graph from the relation.
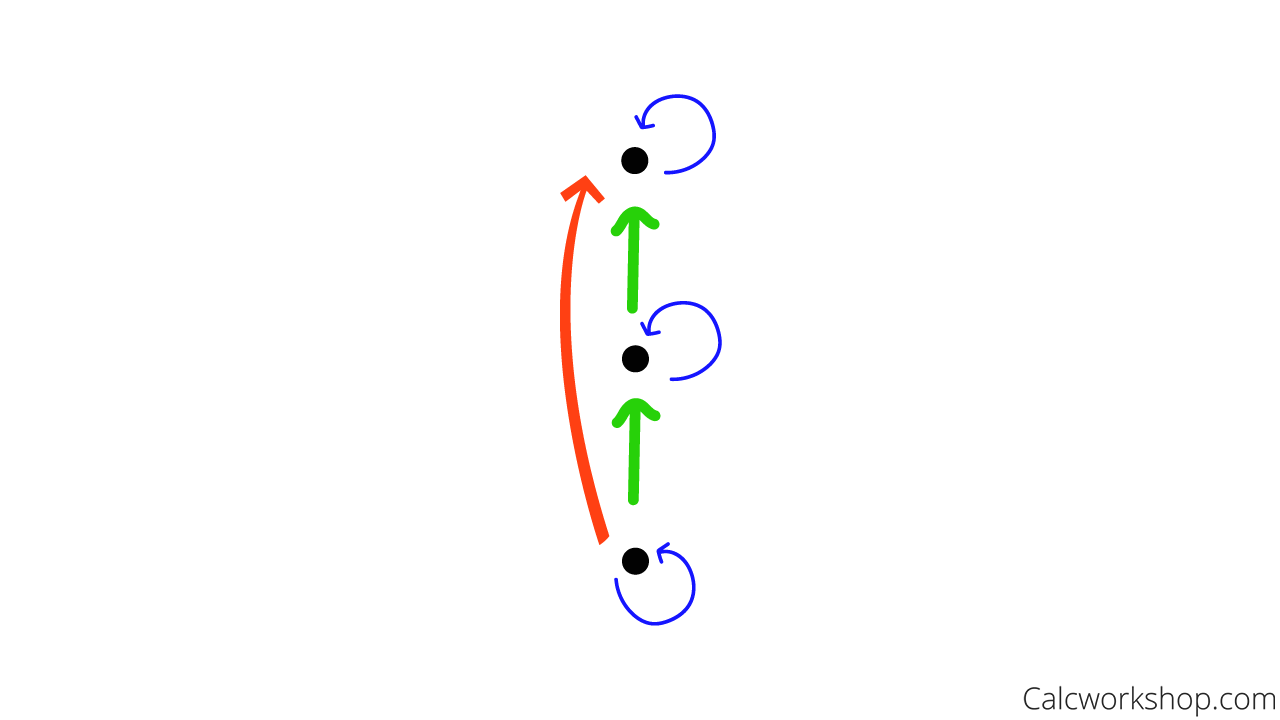
Directed Graph
Step 2
Remove all self-loops.
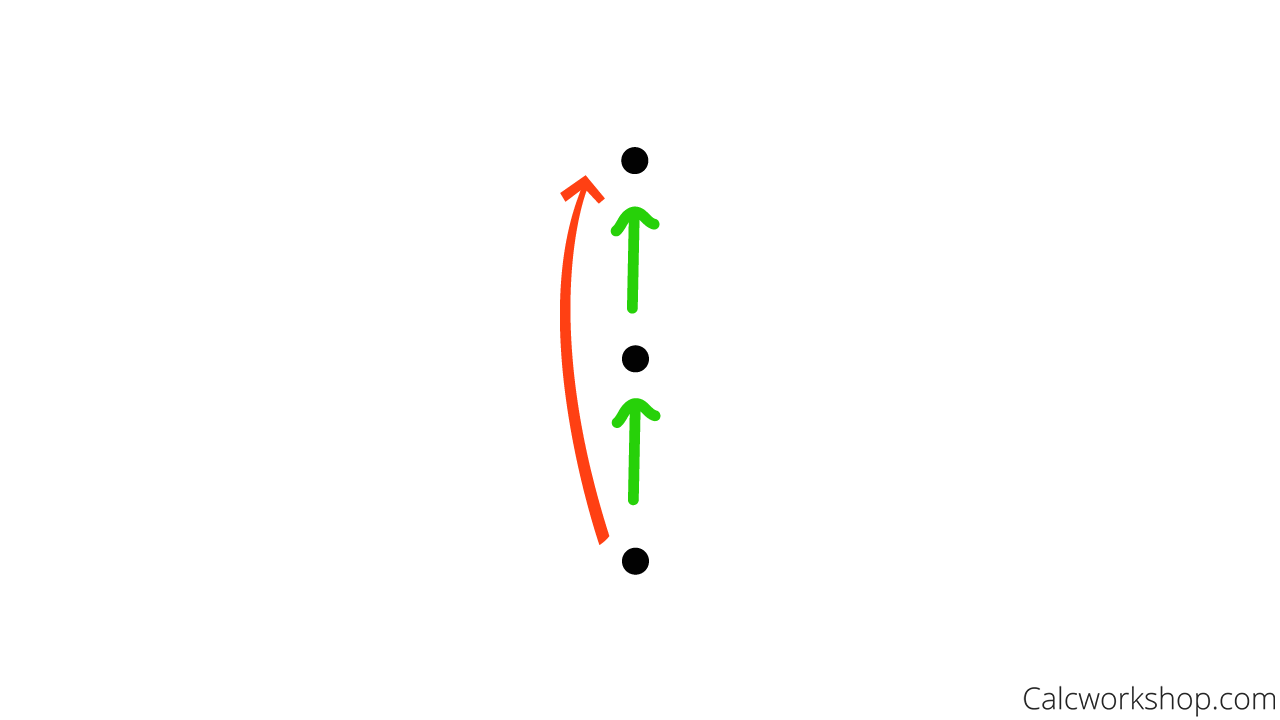
Remove Loops
Step 3
Remove all transitivity.
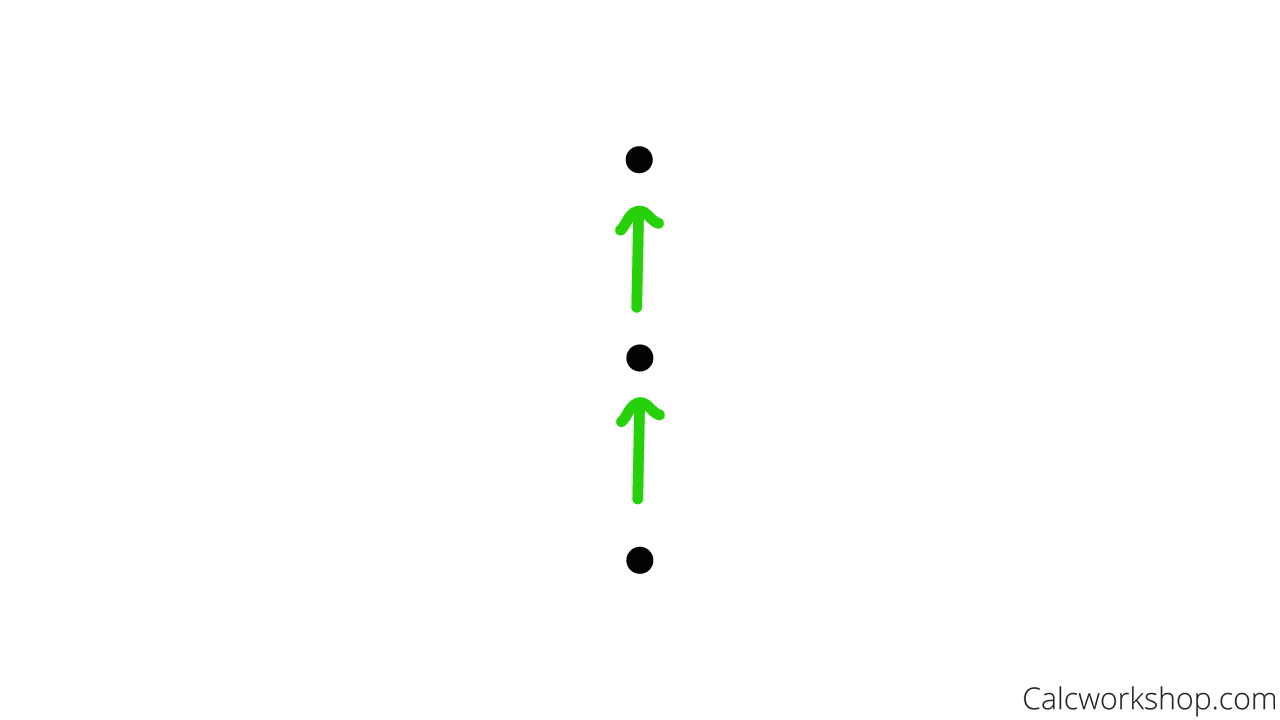
Remove Transitivity
Step 4
Remove orientation (directional arrowheads).
Notice that a Hasse diagram is a “cleaner” more simplified directed graph, as it removes “obvious” or implied edges from the graph.

Remove Directed Arrows
Solved Example
Okay, so let’s draw a Hasse diagram for the poset a ∣ b (a divides b) on {1,2,3,4,6}
First, we construct our relation and create a digraph R={(1,1),(1,2),(1,3),(1,4),(1,6),(2,2),(2,4),(2,6),(3,3),(3,6),(4,4),(6,6)}
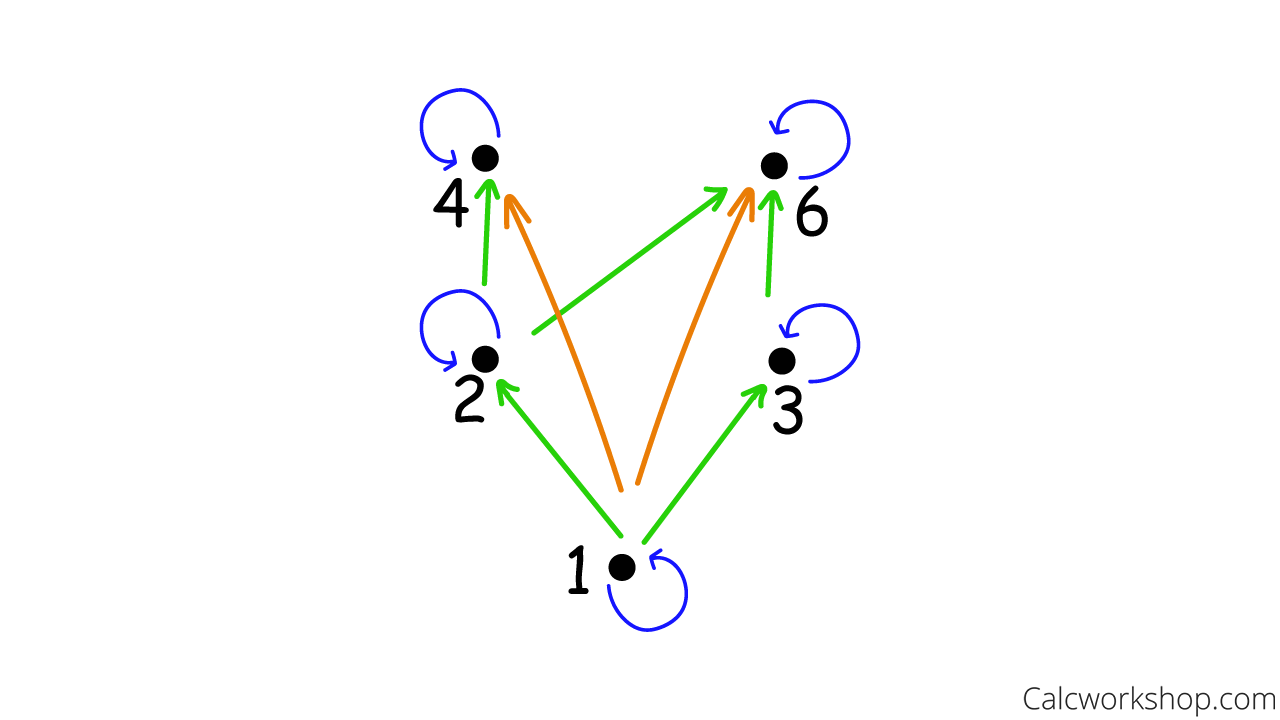
Directed Graph — Divisibility Relation
Now we remove all self-loops, transitivity, and arrowheads.

Hasse Diagram — Divisibility Poset
Now an essential feature of a Hasse diagram is our ability to determine maximal (top) and minimal (bottom) elements of a poset.
Maximal Vs Mininal
A maximal element in a partially ordered set is an element that is greater than or equal to every element to which it is comparable.
Please note that there may be multiple elements to which it is not comparable. And the greatest element in a partially ordered set is an element that is greater than or equal to every element in the set, which means it is comparable to every element in the set.

Maximal and Minimal Definitions
A minimal element in a poset is an element that is less than or equal to every element to which is comparable, and the least element in the poset is an element that is less than or equal to every element in the set. In other words, a least element is smaller than all the other elements.
Worked Example
For each of the following Hasse diagrams, we will decide the maximal and minimal elements of the partial ordering and determine whether the poset has the greatest or least element.

Hasse Diagram — Find The Maximal Minimal Least And Greatest
This means that a poset can have a top, a bottom, both, or neither. And a finite poset always has at least one minimal element and at most one top element.
Together we will learn how to determine if a relation is a partial order by verifying it is reflexive, antisymmetric, and transitive, as well as creating Hasse diagrams and identifying maximal and minimal elements.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 10 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.