Did you know that lattice theory, along with partial order, plays a vital role in combinatorics and number theory and in such applications programming and data mining?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Definition
Formally, a lattice is a poset, a partially ordered set, in which every pair of elements has both a least upper bound and a greatest lower bound. In other words, it is a structure with two binary operations:
- Join
- Meet
But to fully understand lattices and their structure, we need to take a step back and make sure we understand the extremal elements of a poset because they are critical in understanding lattices.
Now, if you recall, a relation R is called a partial ordering, or poset, if it is reflexive, antisymmetric, and transitive, and the maximal and minimal elements in a poset are quickly found in a Hasse diagram as they are the highest and lowest elements respectively.
Example
For example, let A = {1,2,3,6} where a is related to be by divisibility, meaning “a divides b.” Let’s prove that the relation is a partial order, construct a Hasse diagram, and determine its maximal and minimal elements.
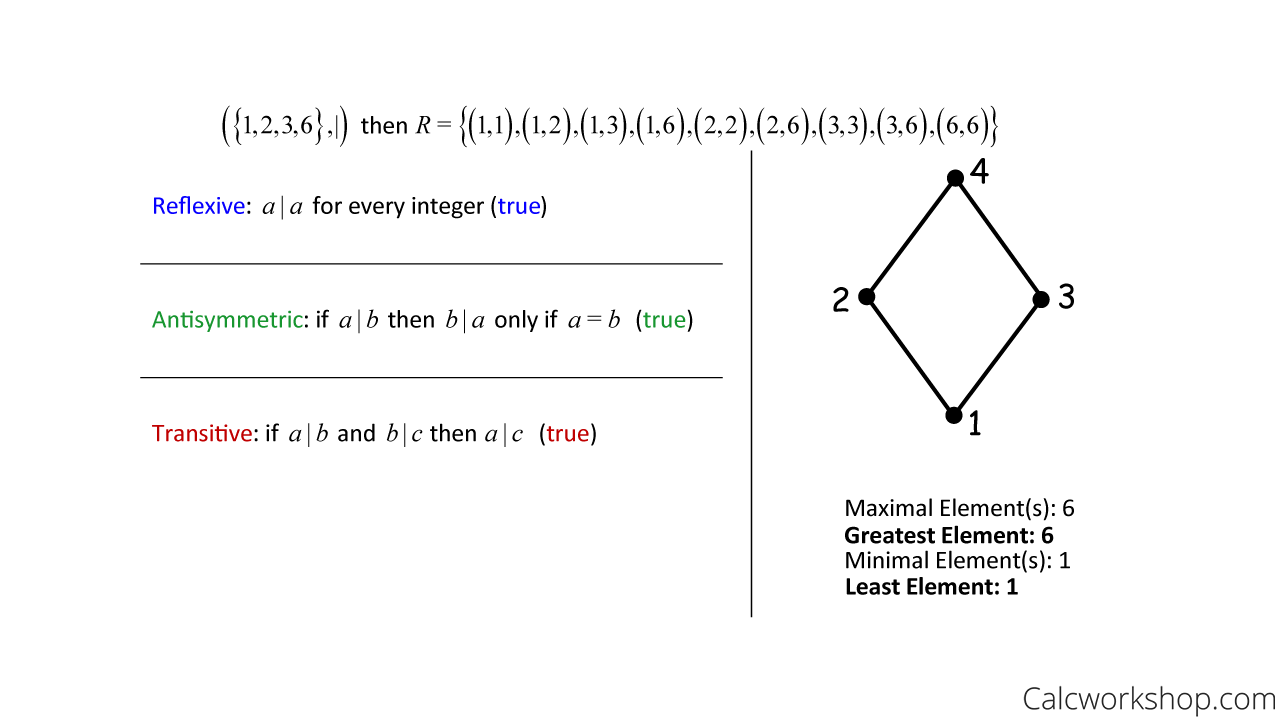
Prove Poset — Maximal and Minimal Elements
And sometimes, we wish to find the upper and lower bounds of a subset of a partial order. An easy way to think of this is to look for downward and upward paths. If a vertex is an “upper bound,” then it has a downward path to all vertices in the subset. And a vertex is a “lower bound” if it has an upward path to all vertices in the subset.
Example
For example, given the following Hasse diagram and subset {e,f}, let’s identify the upper and lower bounds by looking at downward and upward arrows.
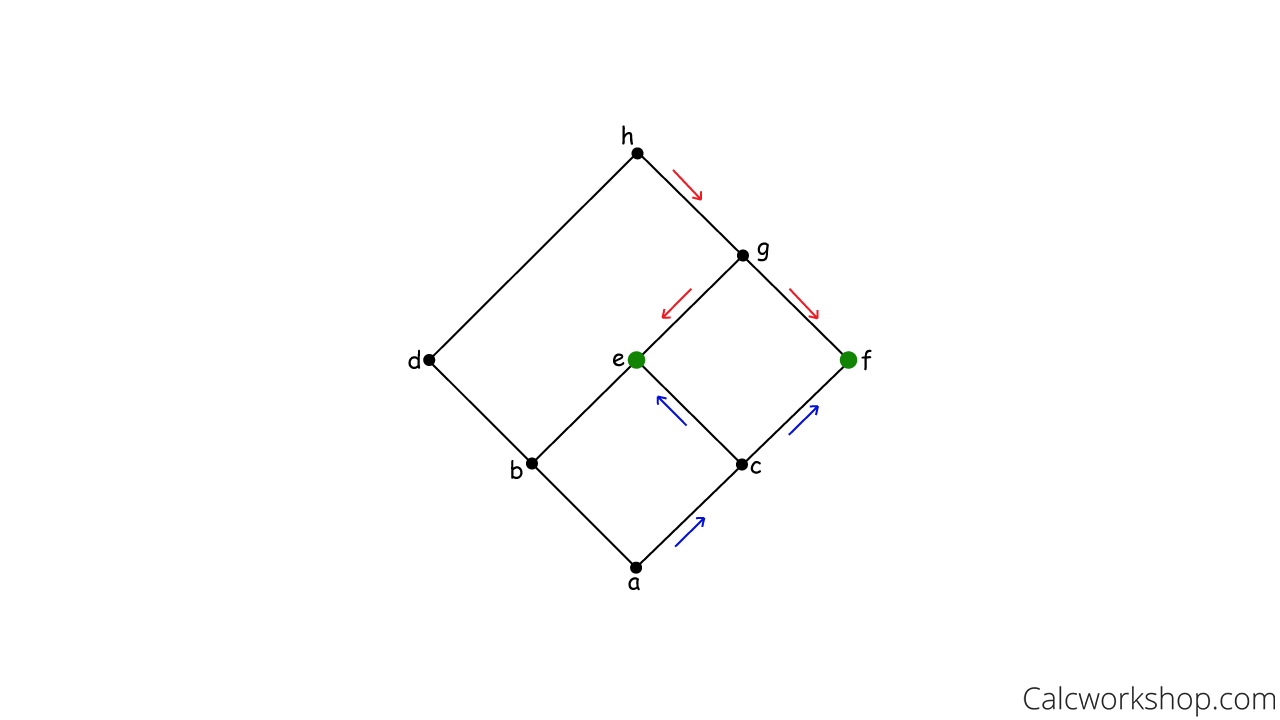
Find Upper Lower Bounds — Partial Order
The upper bound is all those vertices with a downward path to both e and f, namely vertices h and g. And the lower bound is all the vertices that have an upward path to both e and f, namely a and c.
But why is all of this important?
Because a lattice is a poset in which every pair of elements has both a least upper bound (LUB or supremum) and a greatest lower bound (GLB or infimum).
This means that a lattice has to have both an upper and lower bound, and we must be able to find the least upper bound and greatest lower bound.
Using our Hasse diagram from above, notice that our upper bound is {g,h} and that the least of these two vertices (lowest of the upper bound) is vertex g. Therefore, the LUB for this poset is g. Moreover, recognize that our lower bound for this poset is {a,c}, and the greatest of these two vertices (highest of the lower bound) is vertex c. Thus, the GLB is c.
Additionally, a lattice can be described using two binary operations: join and meet.
Of two elements, the join, or sum, is the least upper bound (LUB), sometimes called the supremum or Sup. And the meet, or product, of two elements, is the greatest lower bound (GLB), sometimes called the infimum or Inf.
The table below denotes the LUB and GLB in terms of the join and meet and highlights some alternate notation for each.
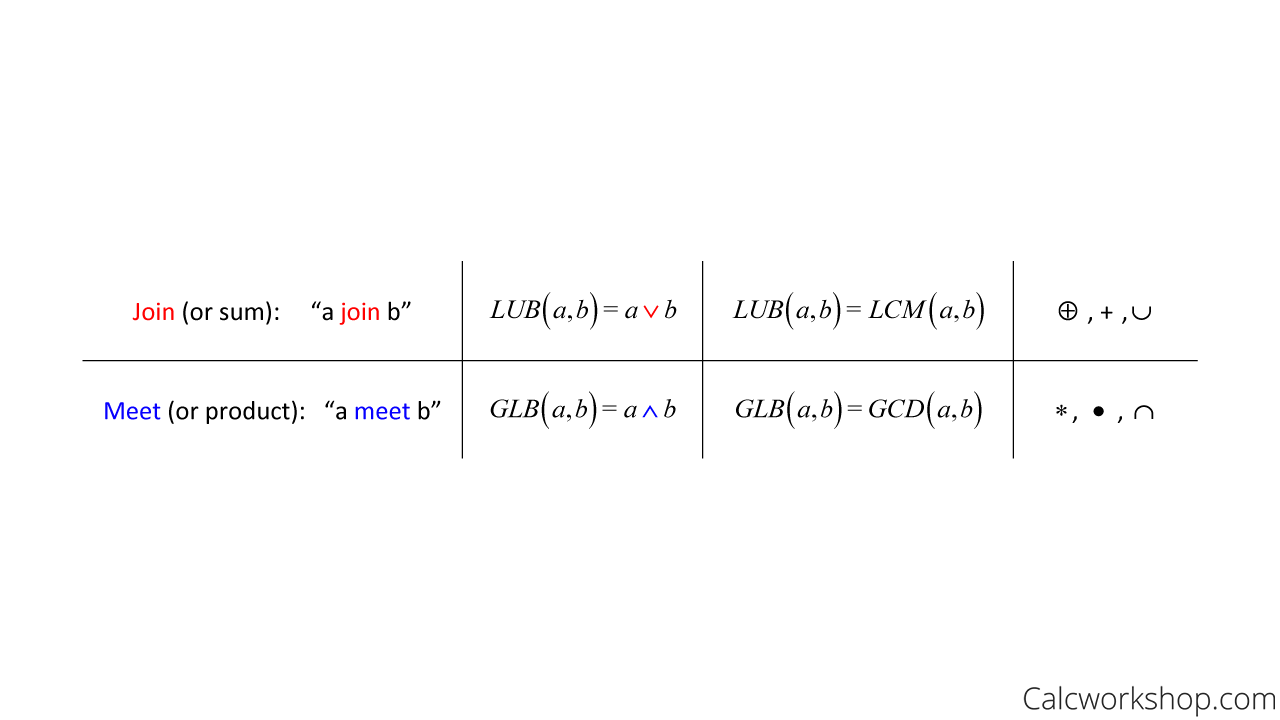
Join Meet — LUB and GLB Notation
But I want to emphasize that the LUB of a pair of two elements is the same as finding the least common multiple (LCM), and the GLB of a pair of two elements is the same as finding the greatest common divisor (GCD)!
Example
For example, suppose we are given the following partial ordering, indicated in the Hasse diagram below, and subset S = {10,15}. Then the least upper bound of 10 and 15 is 30, which is the least common multiple, and the place where 10 “joins” 15. And the greatest lower bound of 10 and 15 is 5, which is the greatest common divisor and the place where 10 “meets” 15.
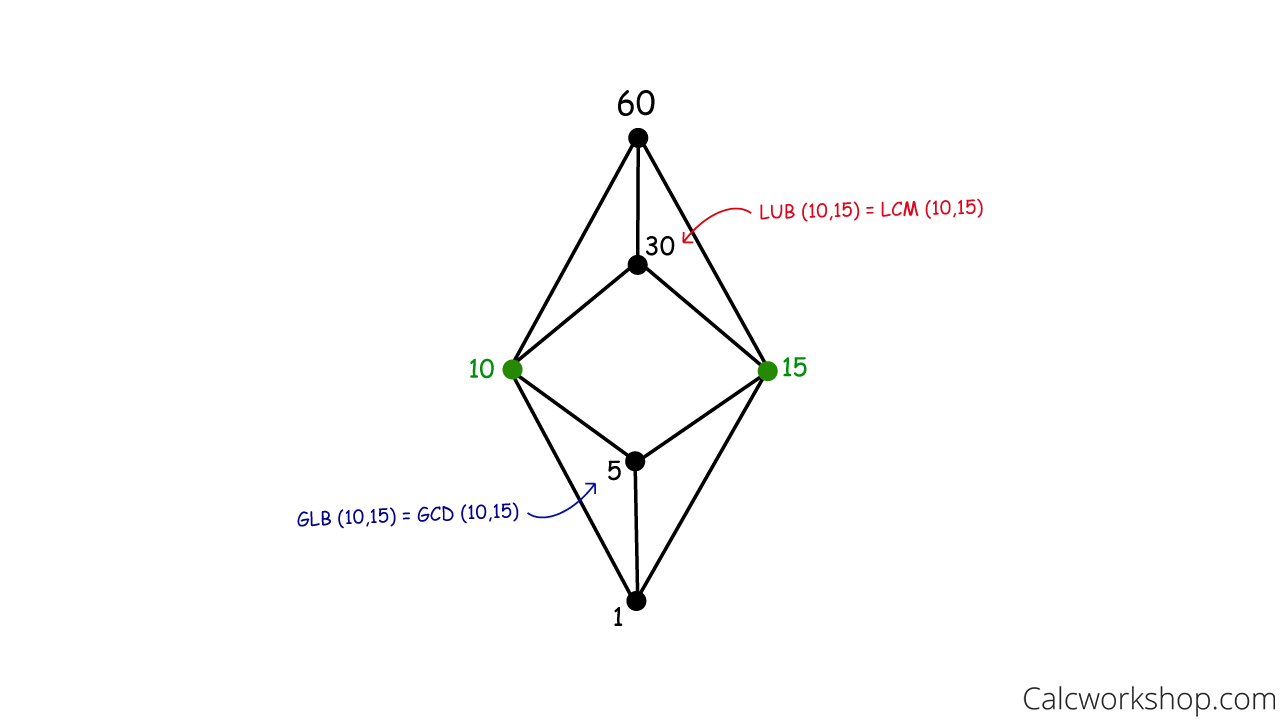
Identify LUB GLB — Poset
It is important to note that not all partially ordered sets are lattices. So, how do we determine whether or not a poset is a lattice?
As we will see in the video below, there are three ways we can show that a poset is or is not a lattice:
- Construct a table for each pair of elements and confirm that each pair has a LUB and GLB.
- Use the “join and “meet method for each pair of elements.
- Draw a Hasse diagram and look for comparability.
Example
For example, let’s determine if the following posets are lattice using a Hasse diagram.

Determine Partial Ordering — Lattice
The partial ordering on the left indicates a lattice because each pair of elements has both a least upper bound and greatest lower bound. In other words, each pair of elements is comparable.
However, the partial ordering on the right is not a lattice because elements b and c are incomparable. Notice that while the upper bound for b and c is {d,e,f,g}, we can’t identify which one of these vertices is the least upper bound (LUB) — therefore, this poset is not a lattice.
Moreover, several types of lattices are worth noting:
- Complete Lattice – all subsets of a poset have a join and meet, such as the divisibility relation for the natural numbers or the power set with the subset relation.
- Bounded Lattice – if the lattice has a least and greatest element, denoted 0 and 1 respectively.
- Complemented Lattice – a bounded lattice in which every element is complemented. Namely, the complement of 1 is 0, and the complement of 0 is 1.
- Distributive Lattice – if for all elements in the poset the distributive property holds.
- Boolean Lattice – a complemented distributive lattice, such as the power set with the subset relation.
Additionally, lattice structures have a striking resemblance to propositional logic laws because a lattice consists of two binary operations, join and meet.

Lattice Properties — Identity Laws
Together we will learn how to identify extremal elements such as maximal, minimal, upper, and lower bounds, as well as how to find the least upper bound (LUB) and greatest lower bound (GLB) for various posets, and how to determine whether a partial ordering is a lattice. And we will prove the properties of lattices.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 44 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.