Did you know there are five properties of relations in discrete math?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s true!
And you’re going to learn all about those qualities in today’s lesson.
Let’s go!
In our previous lesson, we learned that the relationships between the elements of two or more sets are called a relation, and we discussed how to represent a relation using the roster method, incidence matrices, and directional graphs.

Relation Notation
And recall, a Binary Relation from set A to set B is a subset of a cartesian product AxB.
Types of Relations in Math
Now we are going to explore some pivotal properties of a relation R from A to A.
- Reflexive
- Irreflexive
- Symmetric
- Antisymmetric
- Transitive
#1 — Reflexive Relation
If R is a relation on A, then R is reflexive if and only if (a, a) is an element in R for every element a in A. Additionally, every reflexive relation can be identified with a self-loop at every vertex of a directed graph and all “1s” along the incidence matrix’s main diagonal.
Example
For instance, if set A = {a,b} then R is reflexive if and only if R = {(a,a), (b,b)}.
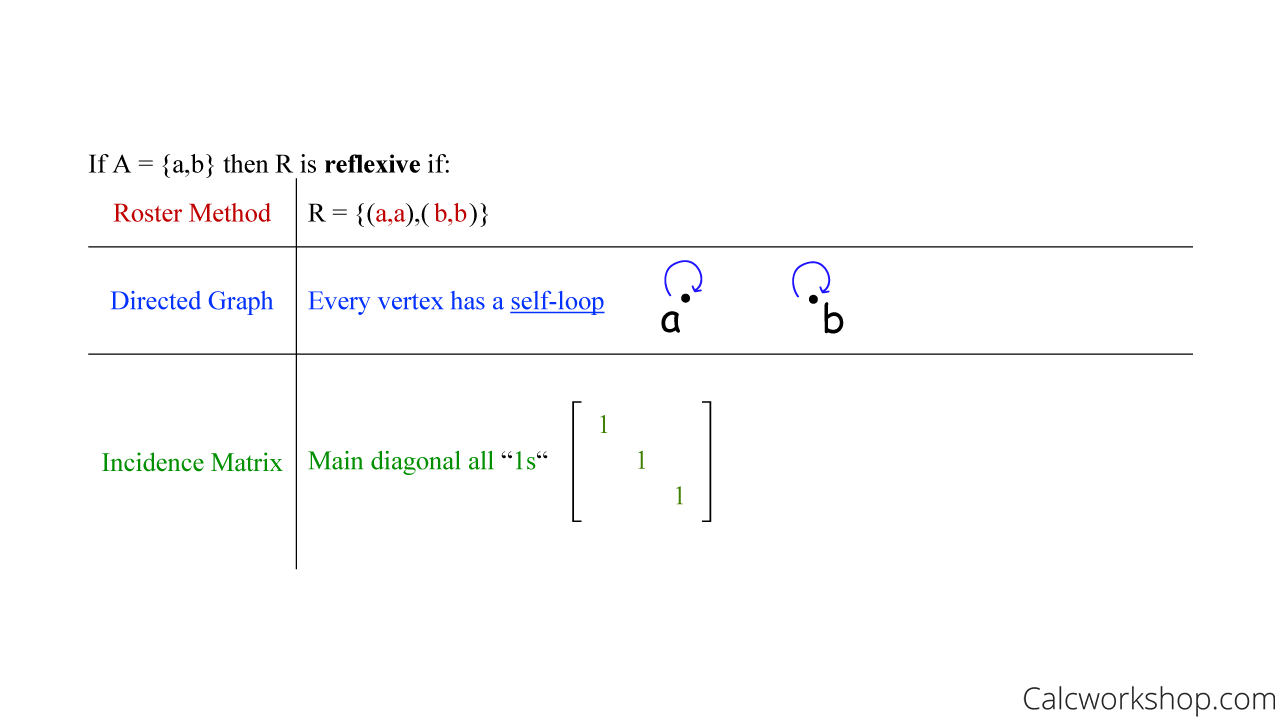
How To Prove A Relation Is Reflexive
#2 — Irreflexive Relation
If R is a relation on A, then R is irreflexive if and only if (a, a) is not an element in R for all a in A. This means, every irreflexive relation will not have self-loops at every vertex of a directed graph, and the main diagonal of the incidence matrix will be all “0s.”
Example
Suppose set A = {a,b} then R is irreflexive if and only if (a,a) and (b,b) are not in R.

Verify Irreflexive Relation
#3 — Symmetric Relation
If R is a relation on A, then R is symmetric if (a,b) is an element in R and (b, a) is also an element of R for all a and b in A. This means, for a symmetric relation, every pair of vertices is connected by none or exactly two directed lines in opposite directions, and the incidence matrix will be a “mirror image” off the main diagonal.
Example
Now, let set A = {a,b} then R is symmetric if

Show Symmetric Relation
#4 — Antisymmetric Relation
If R is a relation on A, then R is antisymmetric if (a,b) and (b,a) are in R only if a = b. So, the only way that both (a,b) and (b, a) are in the relation is if a equals b. Graphically, this means that each pair of vertices is connected by none or exactly one directed line for an antisymmetric relation, and the incidence matrix will not be a “mirror image” off the main diagonal.
Example
In this case, if set A = {a,b} then R is antisymmetric if
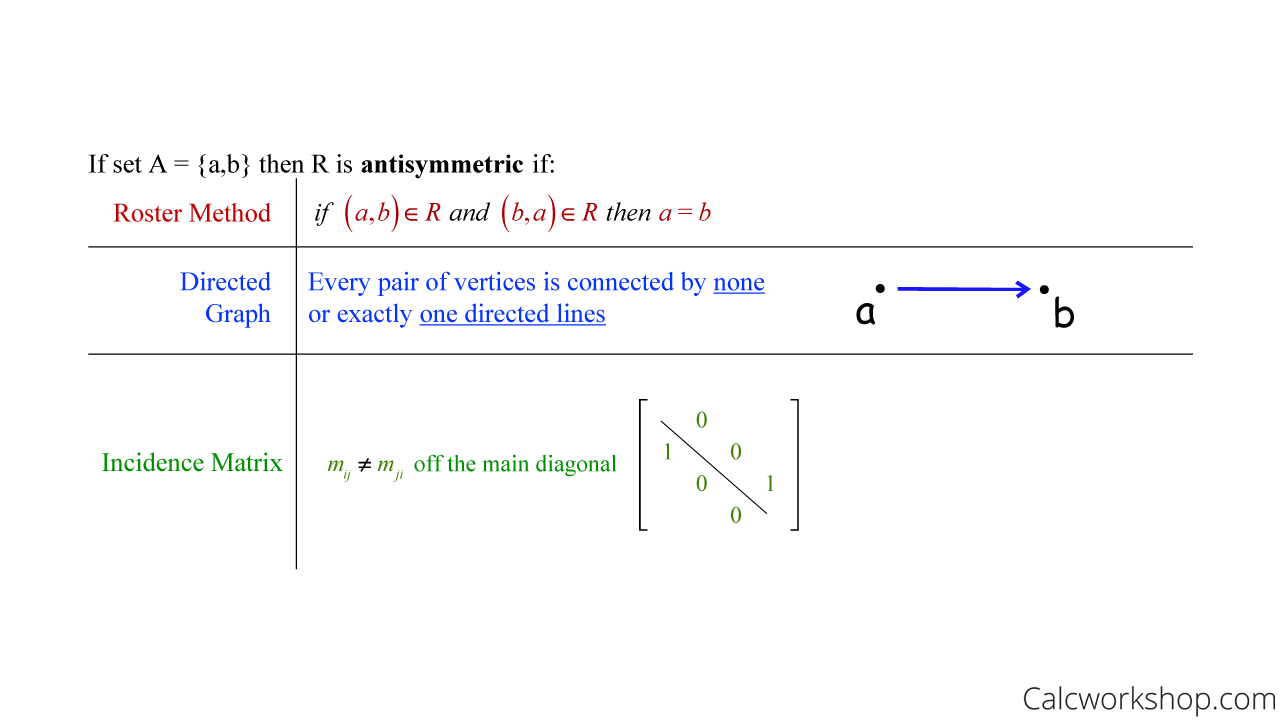
Antisymmetric Relation — Discrete Math
#5 — Transitive Relation
If R is a relation on A, then R is transitive if (a,b) and (b,c) then (a,c) are in R. In other words, for every undirected path joining three vertices a,b, and c, in that order, there is also a directed line joining a to c. And the square of the incidence matrix will reveal a 1 or 2 for every entry corresponding to the original matrix.
Example
So, if set A = {a,b} then R is transitive if

How To Tell If A Relation Is Transitive
It is important to note that a relation can be reflexive, irreflexive, both, or neither. Furthermore, a relation can be symmetric, antisymmetric, both, or neither. Consequently, it’s essential to check every property. The University of Pittsburgh covers relations in discrete mathematics with a handy PDF.
Now that we know our properties let’s look at a few examples.
Suppose set A = {1,2,3,4} and R is a relation on A such at R = {(1,1),(1,2),(2,1),(2,2),(3,3),(4,4)}. Determine which of the five properties are satisfied.
- Reflexive: YES because (1,1),(2,2),(3,3) and (4,4) are in the relation for all elements a = 1,2,3,4.
- Irreflexive: NO, because the relation does contain (a, a).
- Symmetric: YES, because for every (a,b) we have (b,a), as seen with (1,2) and (2,1).
- Antisymmetric: NO, because while we have (1,2) and (2,1), 1 does not equal 2.
- Transitive: YES, because if (1,2) and (2,1) then (1,1) as well as (2,1) and (2,1) then (2,2) are all in the relation.
Now let us determine which of the five properties are satisfied for the relation R on the set of all integers where (x,y) is an element of R if and only if the product of x and y is greater than or equal to one.

Identify Properties Relation — Example
Throughout this lesson, we will successfully identify which properties are satisfied for various relations given roster form, set-builder notation, incidence matrix, or directed graph.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 51 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.