In this critical geometry lesson, you’ll learn all about parallel lines cut by a transversal.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
You’ll gain experience classifying line types, identifying angle relationships, and finally using that knowledge to solve problems for missing angles.
Let jump in!
What Are Parallel Lines?
What comes to mind when you think of parallel lines?
Is it the definition, which states that parallel lines are coplanar and never intersect because they are the same distance apart?
Or perhaps you envision two lines that have the same slope and different y-intercepts as we learned in Algebra?
Or maybe it’s just a visual image like a railroad track or a picket fence.
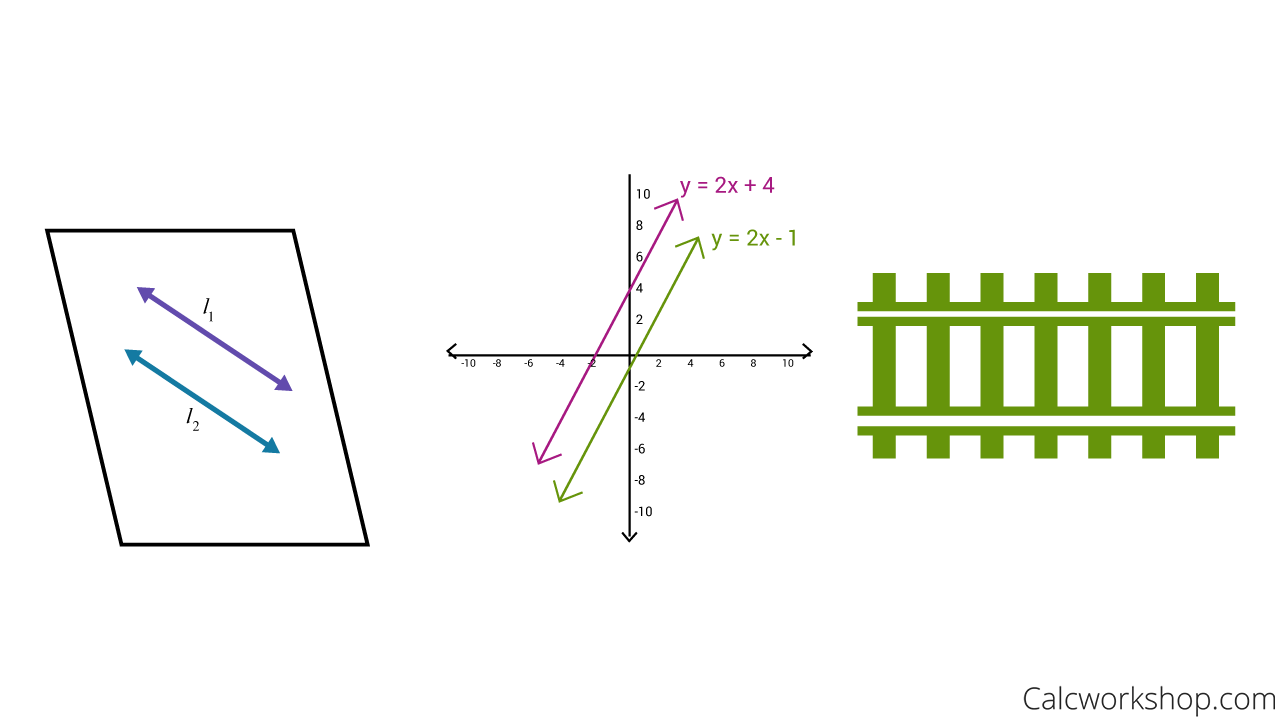
Parallel Lines Examples
What Is A Transversal?
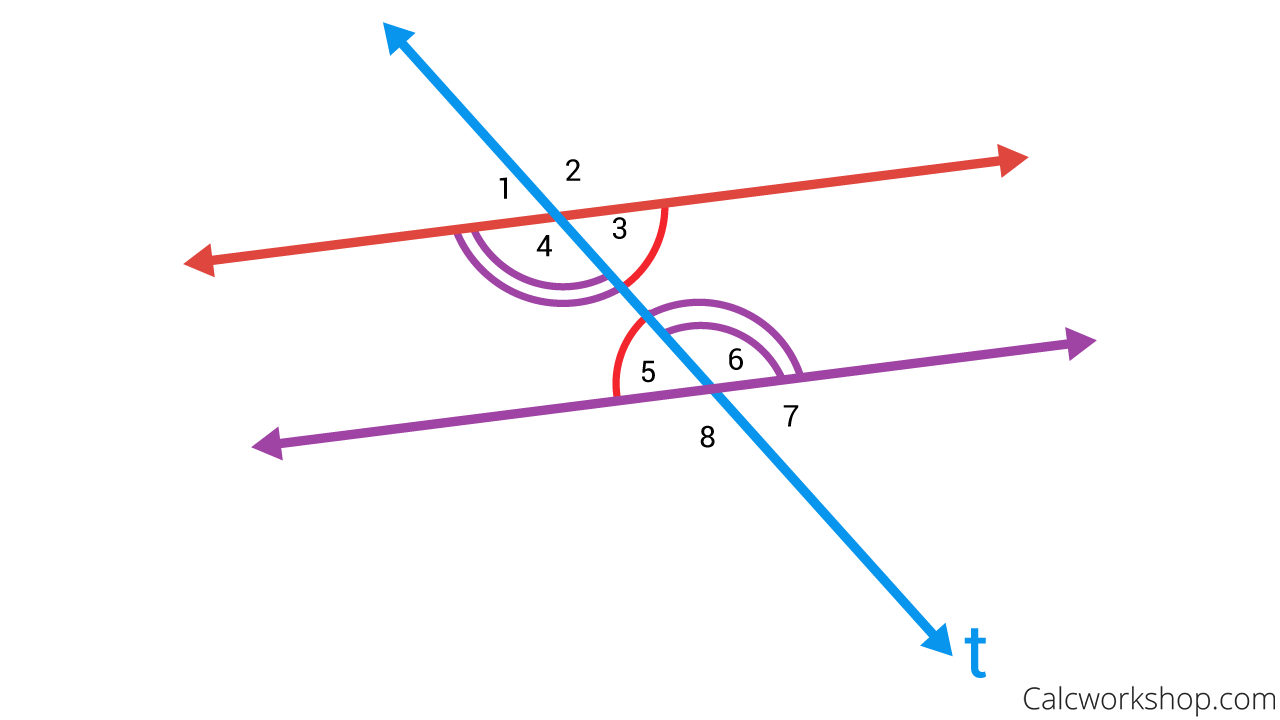
A transversal is a line that intersects two or more coplanar lines, each at a different point.
What this means is that, two lines are intersected by a third line, and in so doing, creates six angle-pair relationships as demonstrated below:
- Interior angles: ∠3,∠4,∠5,∠6
- Exterior angles:∠1,∠2,∠7,∠8
- Pairs of alternate exterior angles: ∠1,∠7 ; ∠2,∠8
- Pairs of alternate interior angles: ∠4,∠6 ; ∠3,∠5
- Pairs of corresponding angles: ∠1,∠5 ; ∠2,∠6 ; ∠3,∠7 ; ∠4,∠8
- Paris of angles on the same-side of the transversal: ∠3,∠6 ; ∠4,∠5
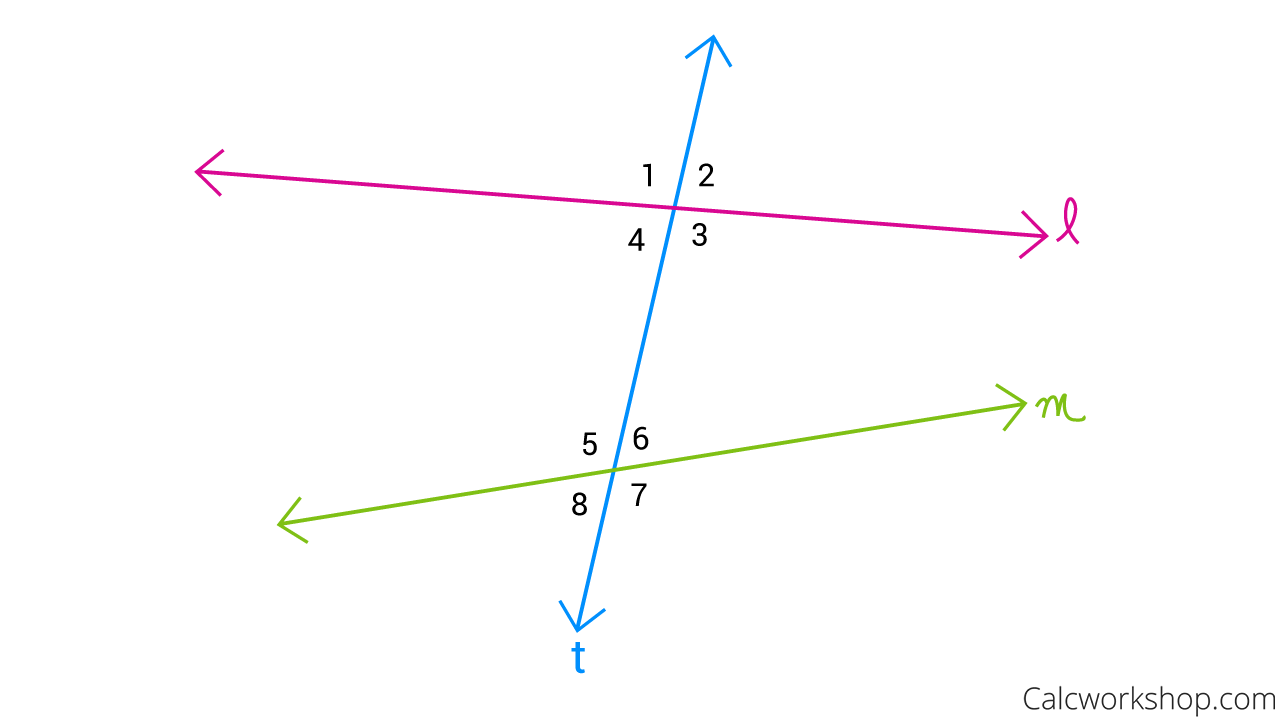
Transversal Line Example
Parallel Lines and Transversals Postulates
Parallel lines and transversals are very important to the study of geometry because they enable us to define congruent angle pair relationships.
How?
Well, when two parallel lines are cut by a transversal (i.e., get crossed by a third line), then not only do we notice the vertical angles and linear pairs that are subsequently formed, but the following angle pair relationships are created as well:
- Corresponding Angles are congruent
- Alternate Exterior Angles are congruent
- Alternate Interior Angles are congruent
- Same Side Interior Angles (Consecutive Interior Angles) sum to 180 degrees
And knowing how to identify these angle pair relationships is crucial for proving two lines are parallel, as Study.Com accurately states.
In the video below, you’ll discover that if two lines are parallel and are cut by a transversal, then all pairs of corresponding angles are congruent (i.e., same measure), all pairs of alternate exterior angles are congruent, all pairs of alternate interior angles are congruent, and same side interior angles are supplementary!
Transversal Angles
Corresponding Angles
∠2 is congruent to ∠6
∠3 is congruent to ∠7
∠4 is congruent to ∠8
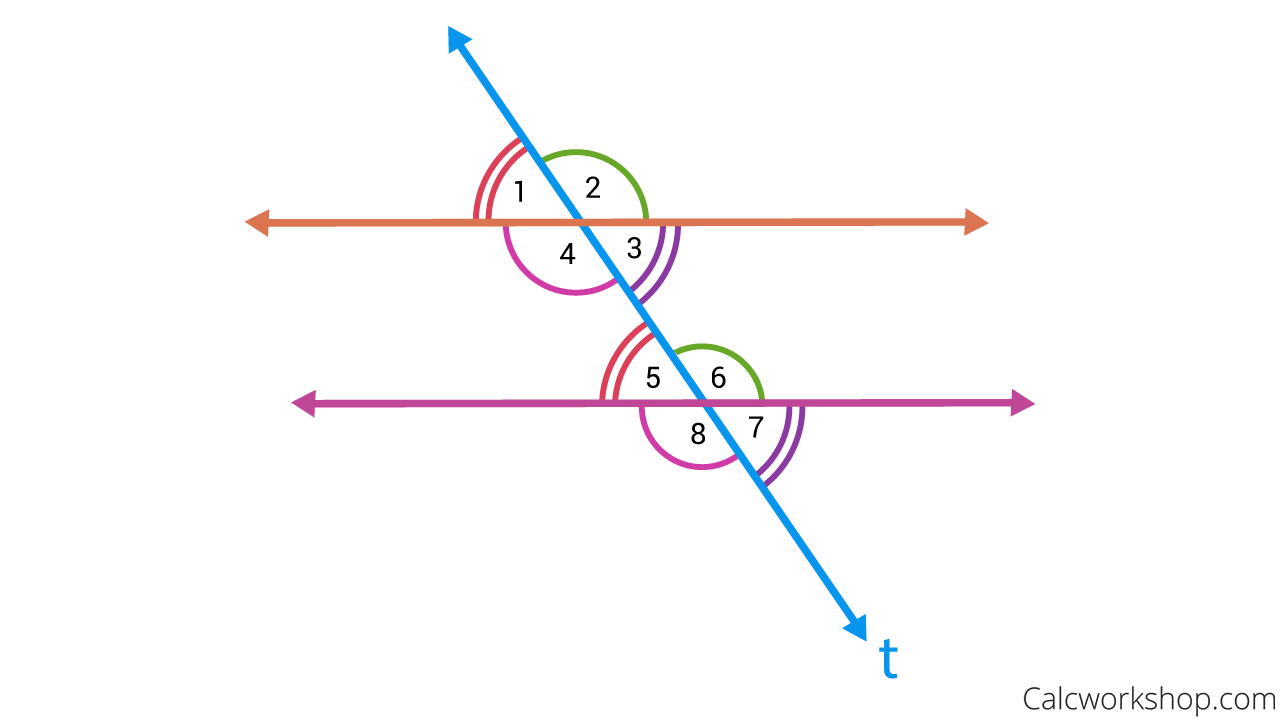
Corresponding Angles
Alternate Exterior Angles
∠2 is congruent to ∠7
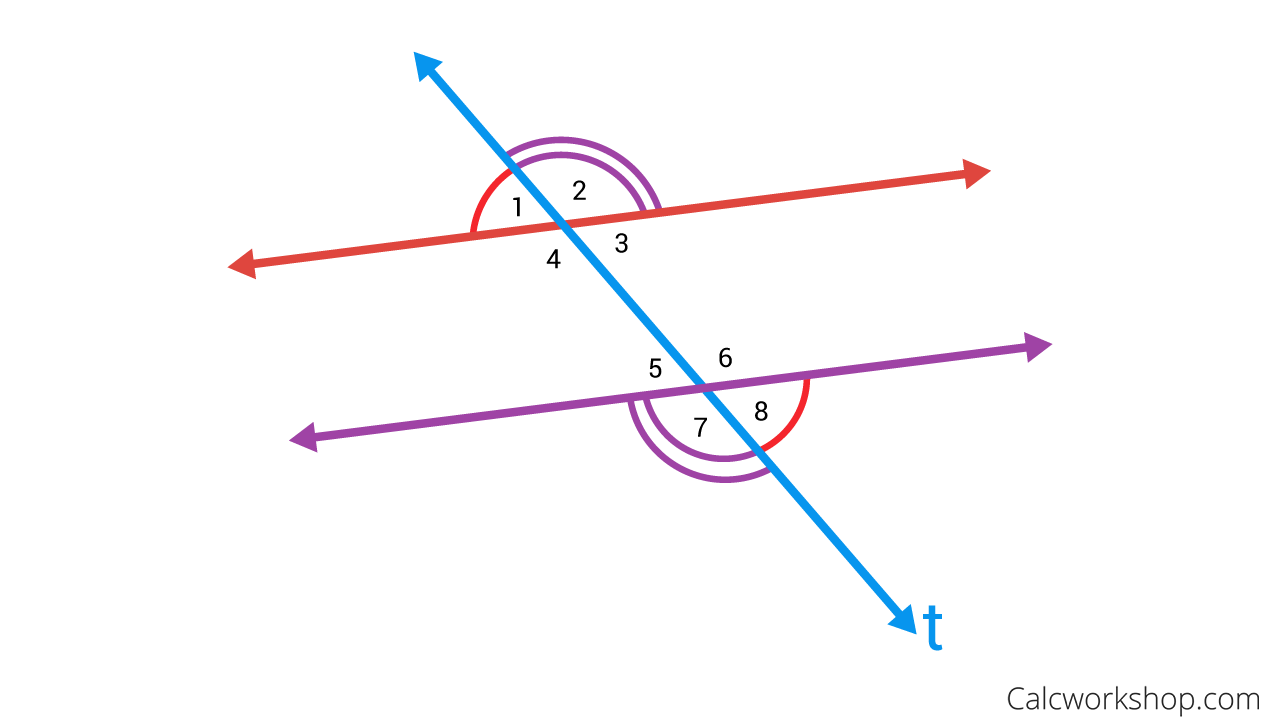
Alternate Exterior Angles
Alternate Interior Angles
∠4 is congruent to ∠6
Alternate Interior Angles
Same Side Interior Angles
∠4 and ∠5 are supplementary

Same Side Interior Angles
Wow!
In the following video, you’ll learn all about classifying lines as parallel, intersecting, or skew. Then you’ll learn how to identify transversal lines and angle pair relationships. Next, you’ll use your knowledge of parallel lines to determine the measure of angles. And lastly, you’ll write two-column proofs given parallel lines.
Parallel Lines Cut By A Transversal – Lesson & Examples (Video)
1 hr 10 min
- What are parallel, intersecting, and skew lines? (Examples #1-8)
- 00:09:34 – Overview of transversal and angle pair relationships (Examples #9-14)
- 00:20:52 – Theorems for perpendicular and parallel lines
- 00:28:47 – Find the measure of each angle given two parallel lines cut by a transversal (Examples #15-18)
- 00:46:05 – Find the measure of each angle (Example #19)
- Exclusive Content for Member’s Only
- 00:49:49 – From the given information can you prove the two lines are parallel? (Example #20)
- 00:55:01 – Write a two-column proof given parallel lines (Examples #21-23)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.