A rational expression is a fraction (ratio) in which the numerator and denominator are both polynomials.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Our goal in simplifying rational expressions is to rewrite the rational expression in its lowest terms by canceling all common factors from the numerator and denominator.
Wait!
What does it mean to “cancel factors”?
Just like we would simplify or reduce a numerical fraction by canceling off factors common to both the top and bottom, we will simplify (reduce) a polynomial fraction by crossing out any factor(s) they have in common.
Now, there is something incredibly important to note: monomials cancel monomials; binomials cancel binomials; trinomials cancel trinomials, etc.
As long as you follow this rule, you’ll steer clear of falling into the cancelation trap!
3 Steps to Simplify Rational Expressions
- Factor completely the numerator and the denominator separately.
- Look for factors that are common to the numerator & denominator. And always remember that we can only cancel factors, not terms!
- Cancel all the common factor(s).
That’s it!
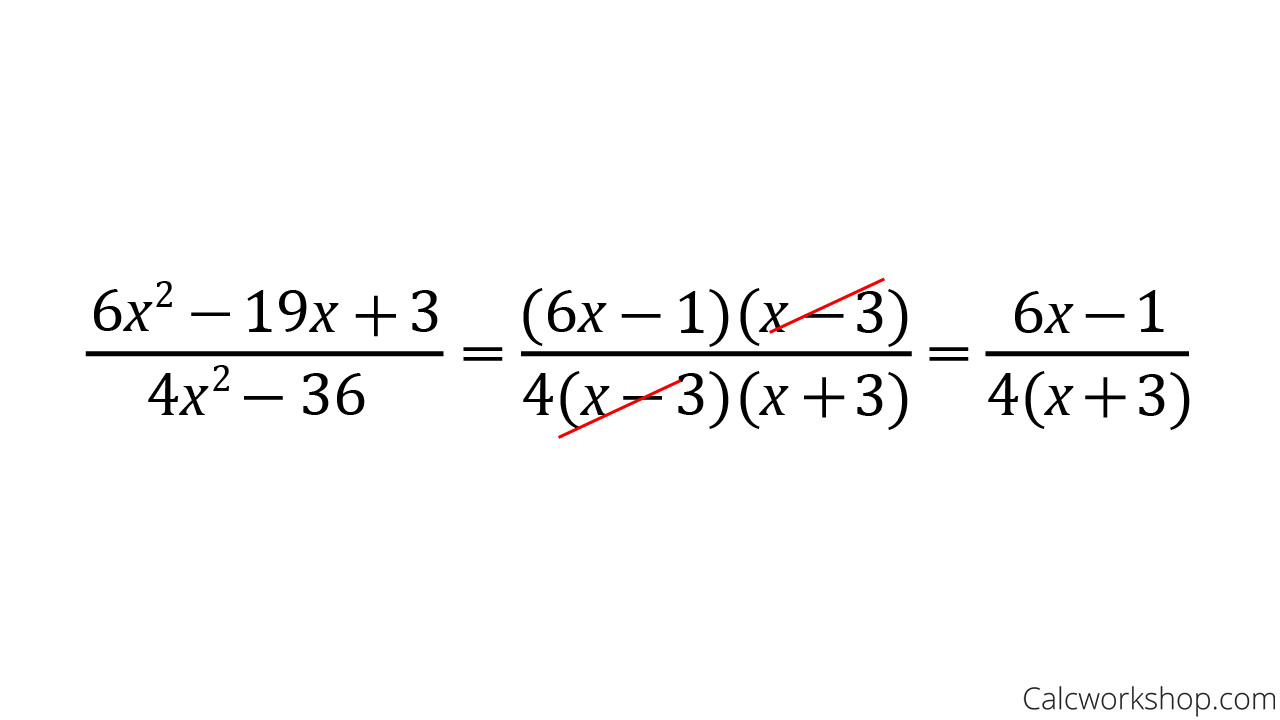
Simplifying Algebraic Fractions Example
We will rely on our knowledge of how to reduce fractions, our exponent rules, and factoring strategies, along with discovering a new skill where we will learn how to factor a minus sign out.
Together, we will find that simplifying rational expressions can be tons of fun!
There’s just one more thing to point out before we jump into the lesson…
As Paul’s Online Notes so accurately states, we know that we can never divide by zero.
Therefore, there is an unspoken rule when dealing with rational expressions: we will always assume that whenever there is a variable in the denominator, it won’t give division by zero.
Phew!
Rational Expressions (How-To) – Video
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.
