In today’s geometry lesson, we’re concluding our study of quadrilaterals, by looking at the properties of trapezoids and kites.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
You’ll learn all the trapezoidal properties needed to find missing sides, angles, and perimeters.
In addition, we’ll explore kites and discuss their associated properties.
Let’s get started!
What Is A Trapezoid?
A trapezoid is a quadrilateral with exactly one pair of parallel sides. The parallel sides are called bases, and the other two sides are called legs.
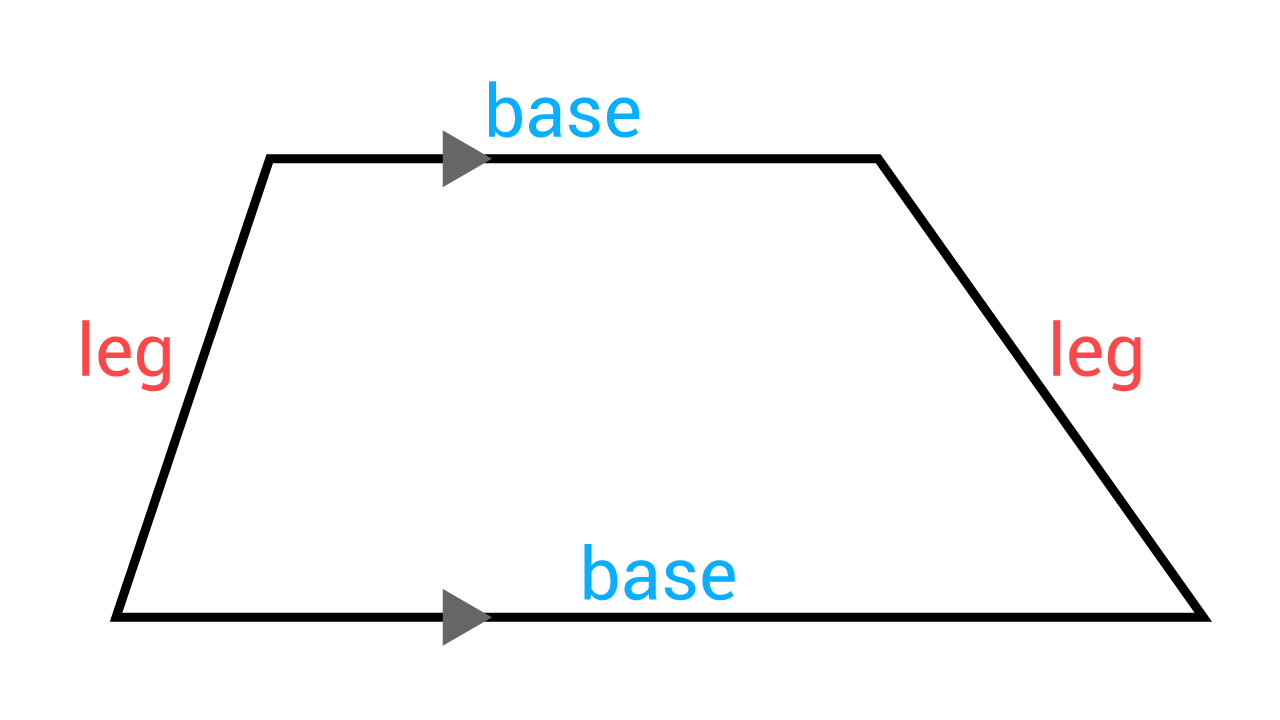
Bases and Legs of a Trapezoid
And because the bases are parallel, we know that if a transversal cuts two parallel lines, then the consecutive interior angles are supplementary. This means that the lower base angles are supplementary to upper base angles.
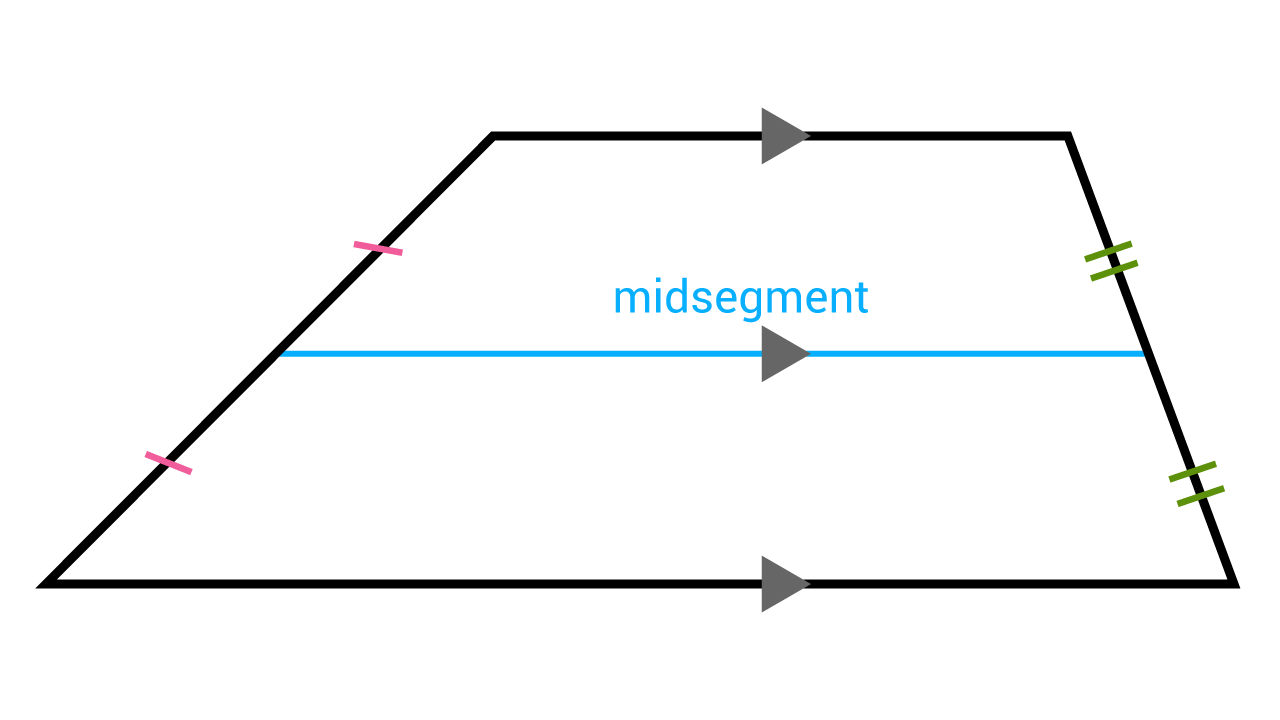
Midsegment of a Trapezoid
Additionally, the midsegment of a trapezoid is the segment joining the midpoints of the legs, and it is always parallel to the bases. But even more importantly, the midsegment measures one-half the sum of the measure of the bases.
And since we know that the sum of all interior angles in a quadrilateral is 360 degrees, we can use our properties of trapezoids to find missing angles and sides of trapezoids.
Cool!
Now, if a trapezoid is isosceles, then the legs are congruent, and each pair of base angles are congruent. In other words, the lower base angles are congruent, and the upper base angles are also congruent. Likewise, because of same-side interior angles, a lower base angle is supplementary to any upper base angle.
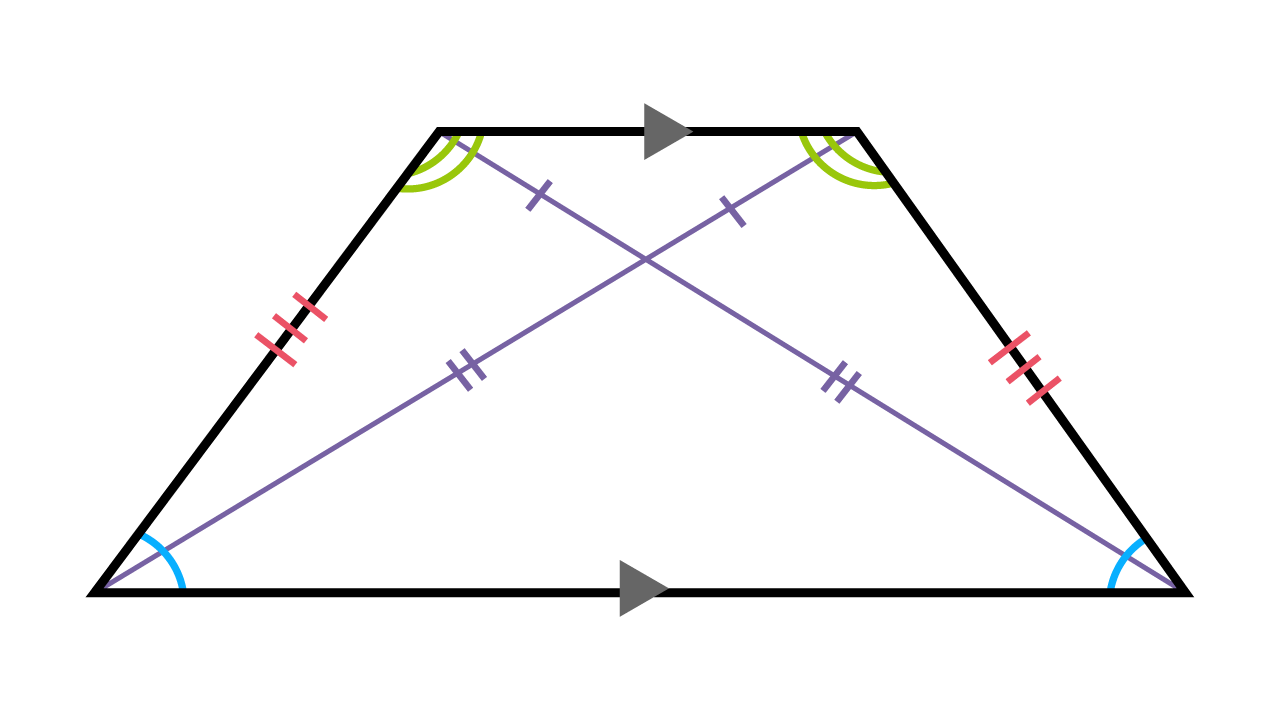
Properties of an Isosceles Trapezoid
But there’s one more distinguishing element regarding an isosceles trapezoid.
A trapezoid is isosceles if and only if its diagonals are congruent. So if we can prove that the bases are parallel and the diagonals are congruent, then we know the quadrilateral is an isosceles trapezoid, as Cool Math accurately states.
In the video below, we’re going to work through several examples including:
- Using these properties of trapezoids to find missing side lengths, angles, and perimeter.
- Determining if the given quadrilateral is a trapezoid, and if so, is the trapezoid isosceles?
What Are The Properties Of Kites?
The first thing that pops into everyone’s mind is the toy that flies in the wind at the end of a long string.
But have you ever stopped to wonder why a kite flies so well?
The way a toy kite is made has everything to do with mathematics!
In fact, a kite is a special type of polygon.
A kite is a quadrilateral that has two pairs of consecutive congruent sides. And while the opposite sides are not congruent, the opposite angles formed are congruent.
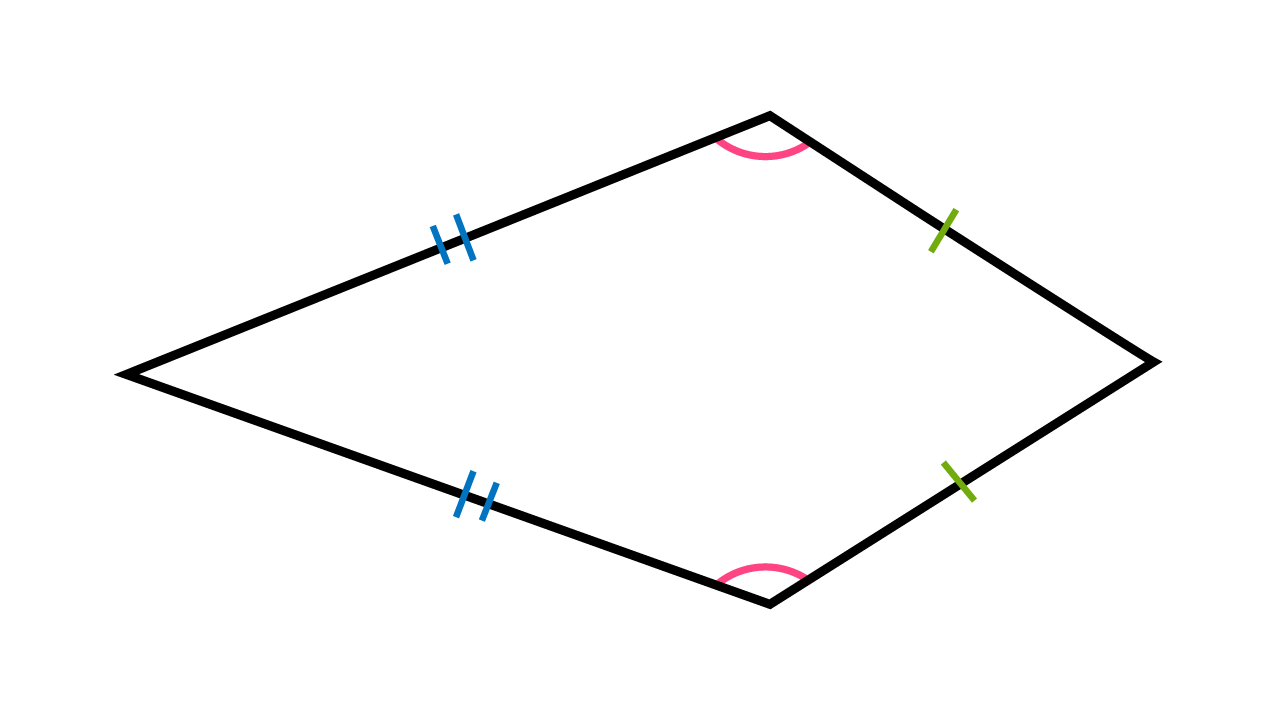
Congruent Sides and Angles of a Kite
Moreover, the diagonals of a kite are perpendicular, and the diagonal bisects the pair of congruent opposite angles.

Perpendicular Diagonals of a Kite
This means, that because the diagonals intersect at a 90-degree angle, we can use our knowledge of the Pythagorean Theorem to find the missing side lengths of a kite and then, in turn, find the perimeter of this special polygon.
This framework of two pairs of consecutive congruent sides, opposite angles congruent, and perpendicular diagonals is what allows for the toy kite to fly so well.
Gosh, doesn’t it make you want to get outside and play?
Trapezoid Properties – Lesson & Examples (Video)
41 min
- Introduction to trapezoids and kites
- 00:00:31 – What are the properties of a trapezoid
- Exclusive Content for Member’s Only
- 00:05:28 – Use the properties of a trapezoid to find sides, angles, midsegments, or determine if the trapezoid is isosceles (Examples #1-4)
- 00:25:45 – Properties of kites (Example #5)
- 00:32:37 – Find the kites perimeter (Example #6)
- 00:36:17 – Find all angles in a kite (Examples #7-8)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.