Sometimes a less formal proof is sufficient for proving an argument.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Existence and Uniqueness proofs are two such proofs.
Both of these proofs rely on our understanding of quantification and predicates.
Because you will be asked to show that “there exists” at least one element for which a predicate is true and how no other element has that particular property.
Mastering Logic Proofs: Existence and Uniqueness
By definition, uniqueness has the following properties:

Uniqueness Definition
Diving Into Existence and Uniqueness: A Step-by-Step Example
For example, suppose x is a real number, and we want to show that 5x + 8 = z has a unique solution.
This style of proof requires just two steps:
- Prove the existence.
- Then prove uniqueness.

Existence And Uniqueness — Problem
As the above proof shows, there is one and only one object, x, with this specified property or solution.
Additionally, when using inference rules to construct a valid argument for a conclusion, we are at liberty to be less formal in our writing as we will create a style similar to a two-column proof from geometry.
Unlocking the Logic Puzzle: A Two-Column Proof Walkthrough
For example, consider the following argument:
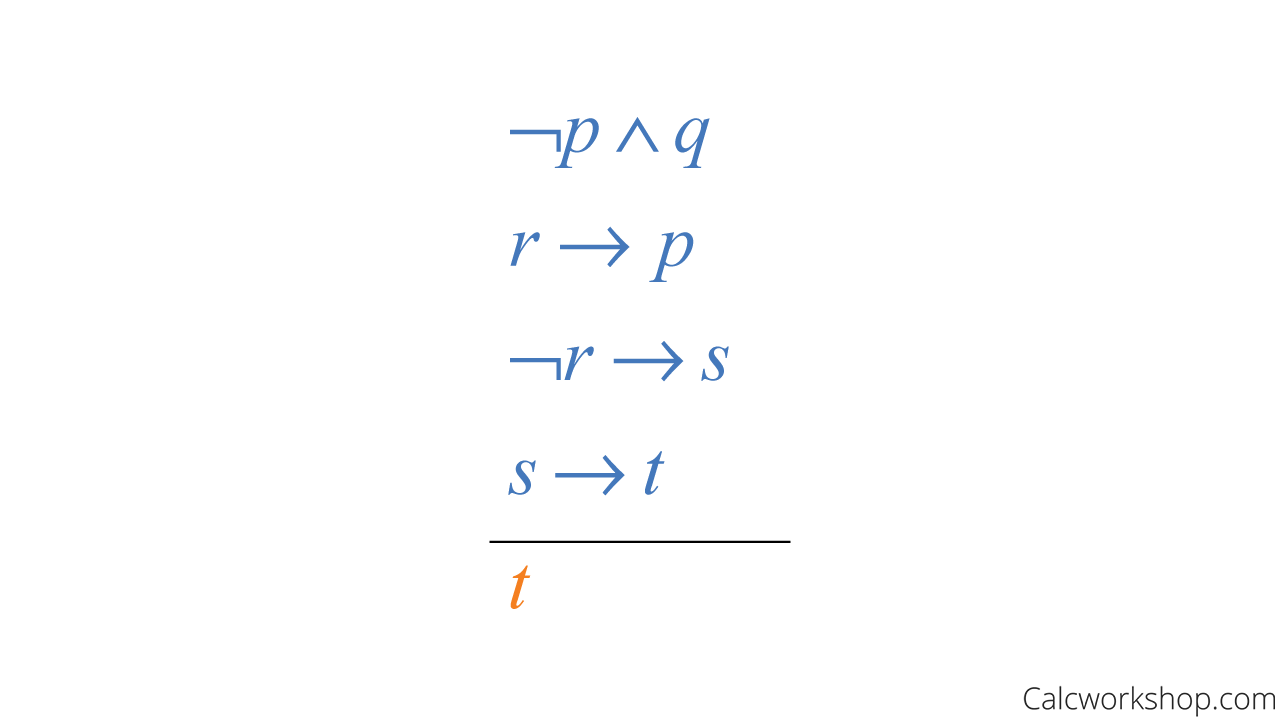
Logic Argument Framework
So, our job is to prove “t” is true using our rules of propositional logic and inference. We do this by creating a two-column style proof, as shown below.
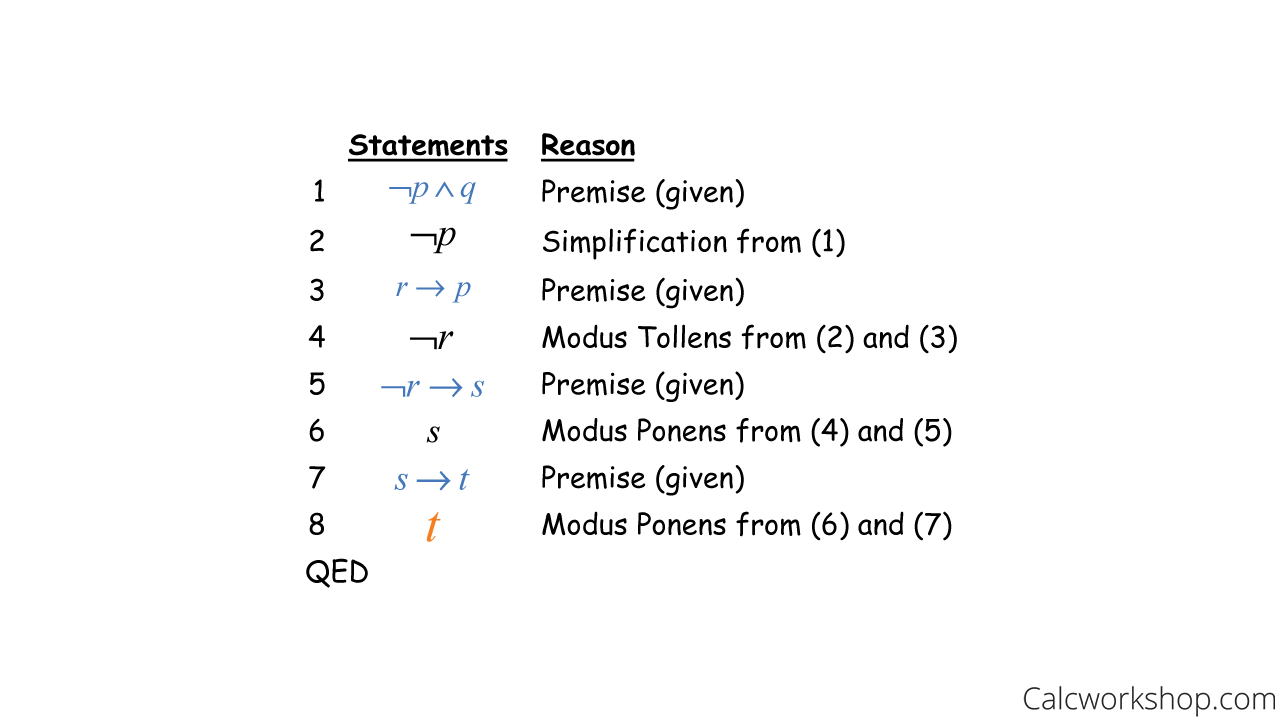
Logical Argument — Proof Structure
Not too bad, but these types of proofs do take a bit to get used to.
From Classroom to Courtroom: A Legal Proof Showcase
Now, let’s look at an example that is a little more involved.
Consider the following argument from a lawyer regarding a defendant’s guilt or innocence.
- If my client is guilty, then the knife was in the drawer.
- Either the knife was not in the drawer or Sparky saw the knife.
- If the knife was not there on January 1st, it follows that Sparky didn’t see the knife.
- Furthermore, if the knife was there on January 1, then the knife was in the drawer and also the hammer was in the barn.
- But we all know that the hammer was not in the barn.
- Therefore, ladies and gentlemen of the jury, my client is innocent.
The first thing we will do is identify our variables.
- C = Client is guilty
- K = Knife in the drawer
- J = Knife was there on January 1st
- S = Sparky saw the knife
- H = Hammer was in the barn
Now we will construct our proof to see if the lawyer’s argument is valid.

Proof of Innocence — Example
As we can see, the lawyer’s well-crafted argument leads the jury to the appropriate conclusion — innocence.
Who knew math and logic proofs would play such a pivotal role in trial outcomes?
By working through examples like these and improving your skills in constructing logical proofs, you’ll gain a better understanding of discrete math.
Summing Up…
But you might be asking yourself, “I understand when I see a proof done for me, but how can I do this on my own?”
The key is practice.
You’re right, these proofs don’t come naturally, and they require you to be a detective on the hunt for the appropriate logic rule to connect the premises (hypotheses) to the conclusion.
That’s why throughout this video lesson, you’ll learn how to construct direct style logic proofs to help make sense of the process and method.
Alright, so grab your inference rules, some paper, and a pencil, and let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 40 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.