So how do you write and structure a direct proof?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Such a good question, and one you’re going to learn all about in today’s discrete math lesson.
Let’s get to it!
In mathematics, proofs are arguments that convince the audience that something is true beyond all doubt.
In other words, a proof is a presentation of logical arguments that explains the truth of a particular statement by starting with things that are assumed to be true and ending with the statement we are trying to prove.
What Is A Direct Proof
A direct proof is a logical progression of statements that show truth or falsity to a given argument by using:
- Theorems
- Definitions
- Postulates
- Axioms
- Lemmas
In other words, a proof is an argument that convinces others that something is true.
A direct proof begins with an assertion and will end with the statement of what is trying to be proved.
How To Write Proofs
So how do we go about constructing a proof?
A proof is a clear and well written argument, and just like a story, it has a beginning, middle, and end.
The beginning of your proof asserts or assumes what we know to be true using definition and theorems. The middle of the proof are statements that follow logically from preceding statements. And the end of our proof is a statement that wish to prove as noted by Virginia Commonwealth University.
But how do you fill in these “logical statements”?
By knowing your audience, grammar, structure, and method.
Audience
Okay, so when I say “know your audience,” all this means is that we need to write in such a way as to always keep your reader in mind.
You don’t want to make too many assumptions as to your reader’s understanding or recollection of particular concepts. Therefore, you need to justify everything, even if it may seem apparent to you, and write in such a way as to explain your reasoning fully.
Additionally, you want to stay away from using such words as “clearly” or “obviously” because while something might be clear or obvious to you, it may not be to your audience. Remember, your goal is to have your reader follow your logic statements from beginning to end without any gaps in understanding.
Grammar
By “know your grammar,” this means you must use symbols and notation appropriately. Proofs are written in complete sentences, using proper punctuation and grammar — thus, they shouldn’t be lazy and put a number or symbol in place of a word or phrase.
Furthermore, we must follow the rules of inference and use definitions, axioms, and theorems precisely. This means we may need to brush up on some vocabulary.

Proof Terminology
Structure
And now, let’s talk about knowing your “structure.”
As we stated above, all proofs have a basic outline: beginning, middle, and end.
The beginning is where we assume something to be true and by stating definitions and necessary theorems.
The middle of our proof will include statements, each following logically from one to the next that will lead the reader to the end.
The “end” is our conclusion and the statement we are trying to prove. Also, it should be pointed out that we write QED, a Latin abbreviation meaning “that which was to be shown,” after our proof to indicate completion.
While this structure seems easy enough, the act of writing a proof can be challenging. Therefore, I would always recommend that you start with a draft, giving yourself the freedom to rethink, revise, and refine your steps if necessary. The key to writing proofs is to take your time, practice, and don’t give up.
Method
Okay, so now that we know the rules for writing a formal proof, it’s now time to talk about “knowing your method.”
We can use several methods or techniques in building a proof, but there are two major groups:
- Direct Proofs.
- Indirect Proofs.
Direct Vs Indirect Proof
Direct proofs always assume a hypothesis is true and then logically deduces a conclusion.
In contrast, an indirect proof has two forms:
- Proof By Contraposition.
- Proof By Contradiction.
For both of these scenarios, we assume the negation of the conclusion and set out to prove either the hypothesis’s negation or a contradictory statement.
Additionally, two other techniques can and will be employed to help us write proofs, such as proof by cases and proof by induction. We will look at all of these types of proofs over the next several videos, but our primary focus for this lesson is to understand Direct Proofs fully.
Direct Proof Definition
So, a direct proof is the most straightforward in its structure. It is constructed using a sequence of simple statements starting with the hypothesis and leading to the desired conclusion.
Here is the formal definition of a direct proof.

Direct Proof Definition
Example #1 – Valid Claim
Alright, so now it’s time to look at some examples of direct proofs.
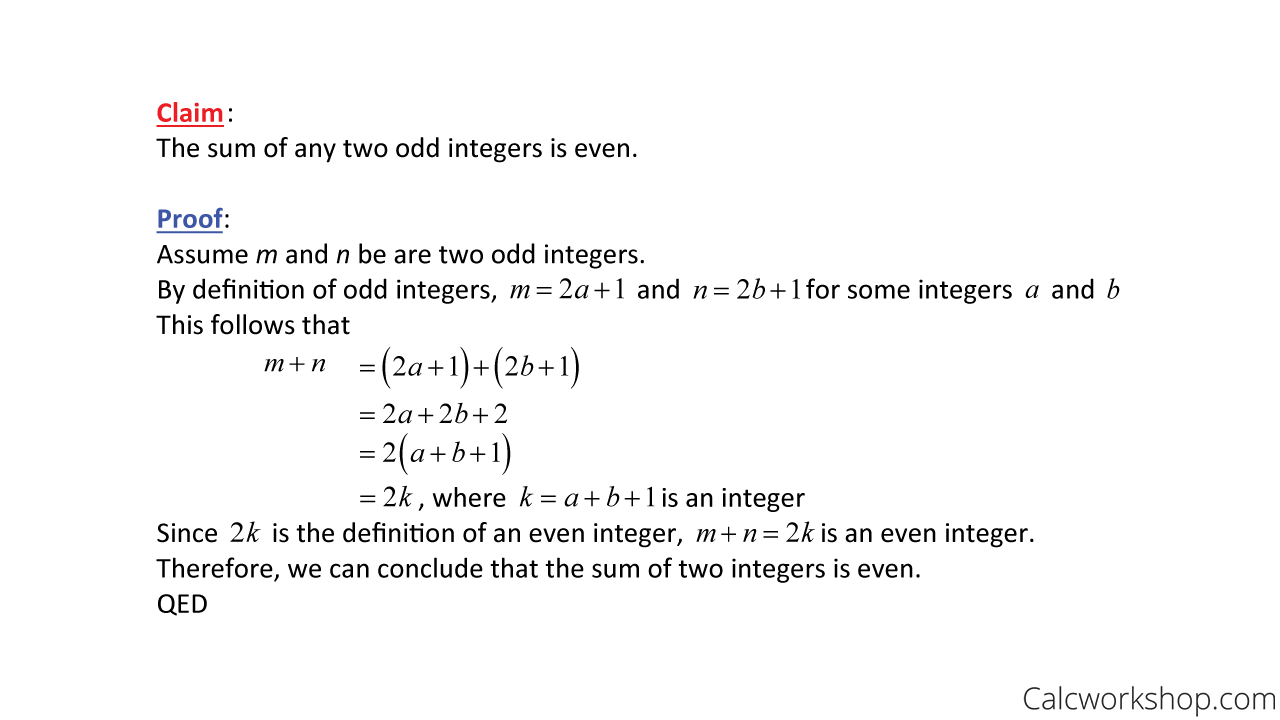
Proof Sum Two Odd Integers Even
Notice that we began with our assumption of the hypothesis and our definition of odd integers. We then showed our steps in a logical sequence that brought us from the theory to the conclusion.
Example #2 – Valid Claim
Let’s look at another example.

Proof Square Even Integer Even
Again, notice how we began with our assumption and basic definition of even integers and followed a logical progression to our rightful conclusion.
But sometimes, we are asked to prove an invalid claim. What do we do then?
We find a counterexample!
A counterexample is just one example showing the claim to be false. While there may be many examples to choose from, all you need is one.
Let’s see how we would use a counterexample to refute a claim.
Example #3 – Invalid Claim
Prove by counterexample.

Proof By Counterexample
Together we will work through numerous examples of how to construct a direct proof, and we will also learn how to use a counterexample to disprove a claim successfully.
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 38 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.