What is a sample space?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s a fundamental aspect of statistics and that’s what we’re going to discuss in today’s lesson.
So jump on in!
Law Of Large Numbers
Did you know that chance behavior is unpredictable in the short run but has a regular, predictable pattern in the long term?
For example, if you flip a coin ten times, the number of heads you get can vary. But if you flip a coin 100 times, the number of heads will be close to 50.
Why?
It’s called the Law of Large Numbers.
All this means is that the more repetitions that occur, the proportion of times that a specific event (i.e., head or tails) will occur approaches a single value. So, for our coin-flipping example, the percentage of heads we would expect to see if we flip the coin 100 times is approximately 0.5 of 50%.
Additionally, this means that probability, or the likelihood of something happening, is a number between 0 and 1 and describes the proportion of times that an outcome will occur over many repetitions (i.e., in the long run).
Sample Space And Events
And this leads us to sample spaces and events.
What is the sample space? And what is an event?
A sample space is the set of all possible outcomes of a statistical experiment, and it is sometimes referred to as a probability space. And outcomes are observations of the experiment, and they are sometimes referred to as sample points. An event is a subset of a sample space as discussed by Shafer and Zhang.
So, in our coin-flipping example, the probability space for flipping a coin one time is “Heads or Tails,” and we write this as S = {H,T}.
How To Find Sample Space?
The three most common ways to find a sample space are:
- To List All the Possible Outcomes.
- Create a Tree-Diagram.
- Use a Venn Diagram.
For example, let’s suppose we flip a coin and roll a die.
- How many outcomes are possible?
- What is the probability space?
- Identify the events.
When we flip a coin, there are only two possible outcomes {heads or tails}, and when we roll a die, there are six possible outcomes {1,2,3,4,5,6}.
That means we have two events:
- One event consists of “heads and tails.”
- The other event consists of {1,2,3,4,5,6}.
1. List Of All Possible Outcomes
Now, let’s see if we can find the sample space.

Example – Flipping A Coin And Rolling A Die
If we flip and roll, then we can get any of the following scenarios:
- Heads and 1
- Heads and 2
- Heads and 3
- Heads and 4
- Heads and 5
- Heads and 6
- Tails and 1
- Tails and 2
- Tails and 3
- Tails and 4
- Tails and 5
- Tails and 6
Or more simply stated in a sample space {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}.
What we’ve just done is to list all the possible outcomes of flipping a coin and rolling a die.
And if you notice, we were able to find 12 possible outcomes for this particular experiment.
2. Tree Diagram
As previously stated, this can also be represented in the form of a Tree diagram, as illustrated below. Each branch indicates a way of achieving the desired outcome and nicely demonstrates all the possible results clearly.
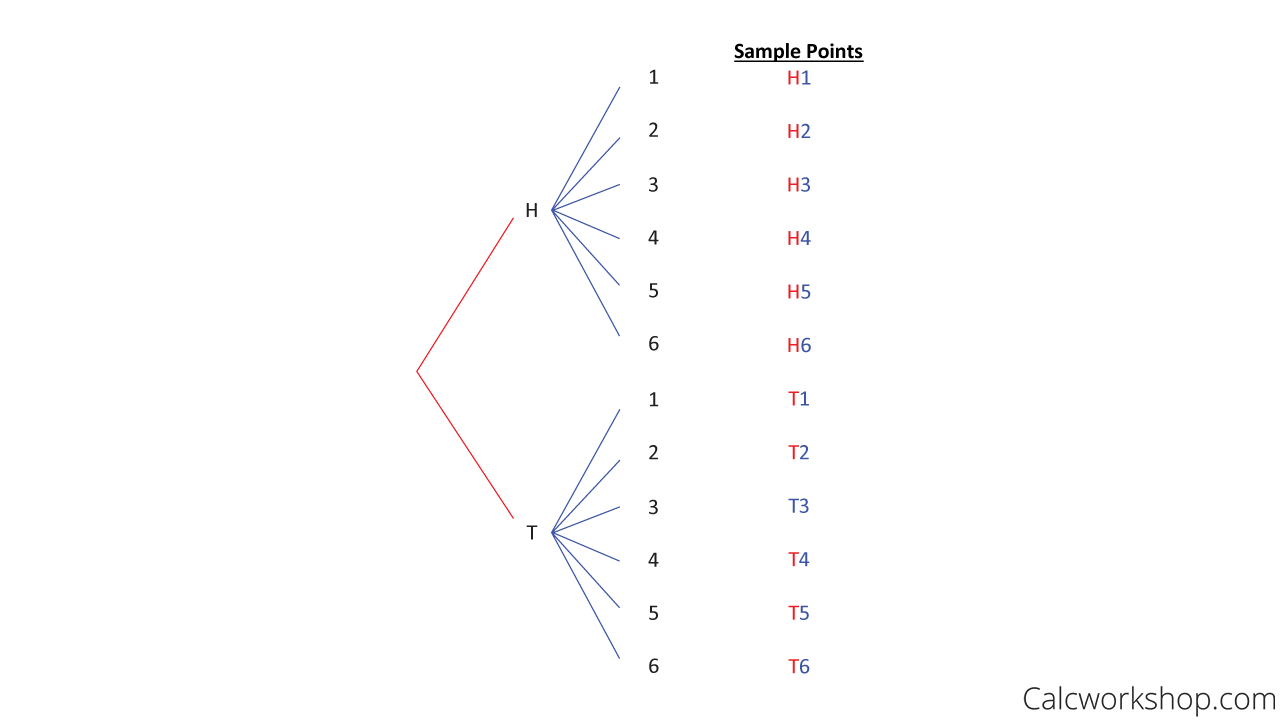
Sample Space Tree Diagram
3. Venn Diagram
Moreover, we could have illustrated the sample space by using a Venn Diagram as well. We would let one circle represent all the possible outcomes of flipping a coin {H, T}, and the other circle represent the six possible outcomes for rolling a die {1,2,3,4,5,6}. The overlap demonstrates the possibility for a single event to occur, such as H2 or T5.
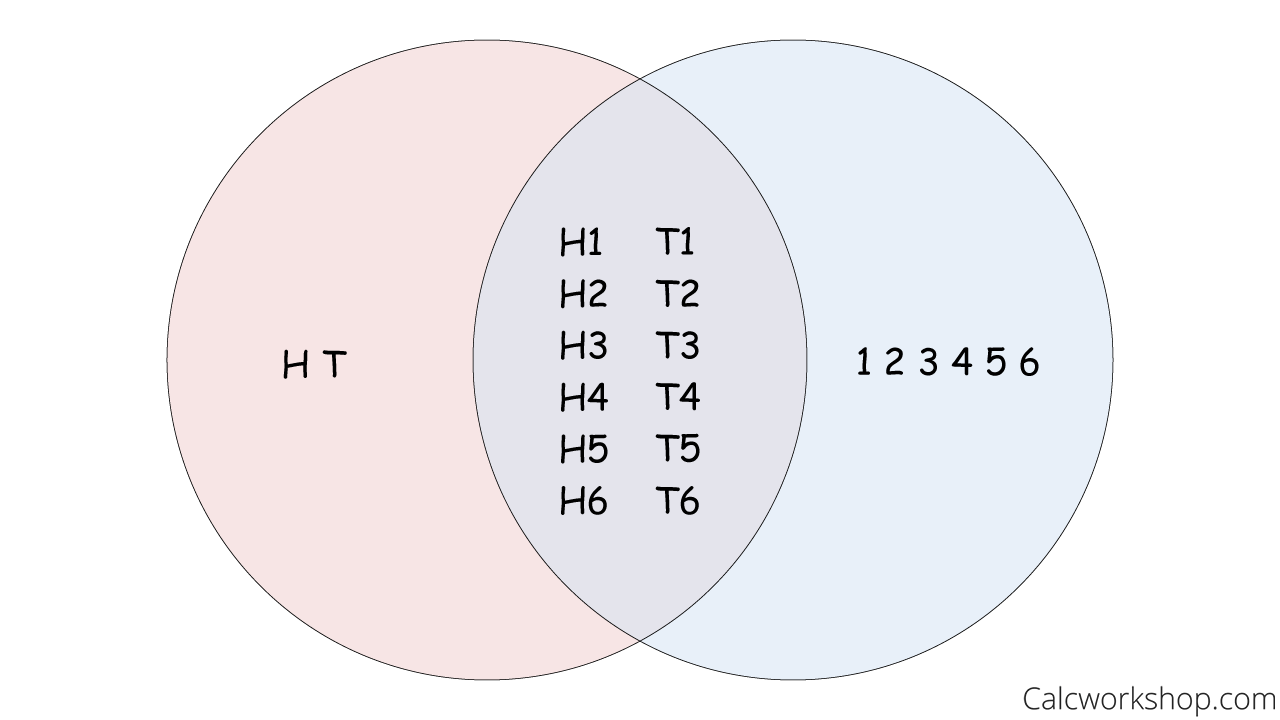
Sample Space Venn Diagram
Fundamental Counting Principle
And this brings us to an important concept: The Counting Principle.
The counting principle, sometimes referred to as the counting rule or multiplication principle, is an easy way to figure out the number of possible outcomes (i.e., sample space). In other words, it is how we calculate the sample space.
All we have to do is multiply the events together to get the total number of outcomes. Using our example above, notice that flipping a coin has two possible results, and rolling a die has six possible outcomes. If we multiply them together, we get the total number of outcomes for the sample space: 2 x 6 = 12!
Cool!
However, there are times when listing the probabilities is too difficult as the sample space is vast. When we encounter large sample spaces, with a large or infinite number of sample points, it is best to describe outcomes by statement or rule.
Finite Vs Infinite
But first, let’s notice the difference between finite sample spaces and infinite sample spaces.
A person plays the lottery, which means they will either win or lose. This is a finite space with two sample points. Or let’s say a survey is taken in a class ranking the course on a scale from 0 to 5. This is also a finite probability space, as there are six sample points. But what if you want to determine the set of all points inside a hot air balloon? Technically there is an infinite number of possible points inside the balloon; thus, making the sample space limitless. When this happens, we will use a rule or statement like x > 0 or “all positive real numbers.”
Complement Rule
And sometimes, we want to identify those elements that are not part of an event. This is called the complement rule.
So, for our coin-flipping example. If we flip a coin and want to count the number of heads, then the complement is the number of tails (i.e., NOT heads).
Here’s another example. Suppose we roll a fair die, so the sample space is S={1,2,3,4,5,6}, and we want to find all the even numbers. So, we define event A to be all the even numbers, which is A={2,4,6}. This means the complement of A would be all the elements that are NOT even, so we say A’={1,3,5}.
We denote the complement of an event as:
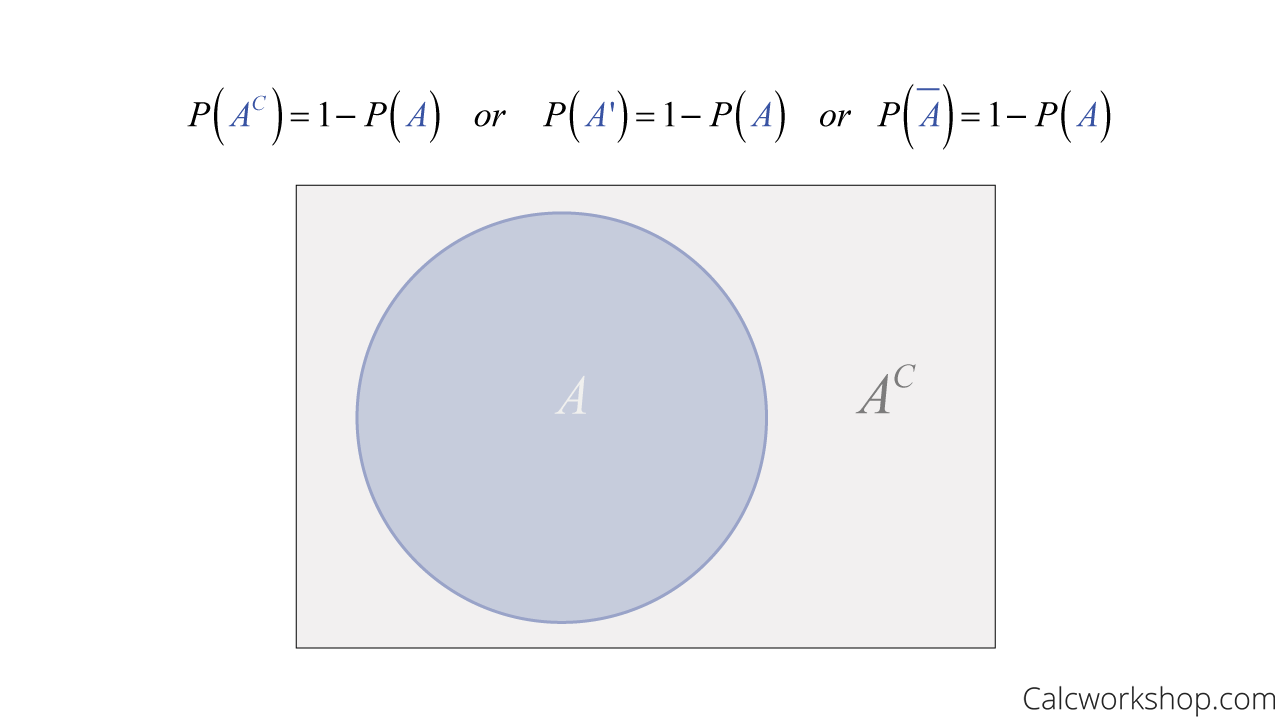
Complement In Probability
Union Vs Intersection
And sometimes we want to know the intersection or union of two events.
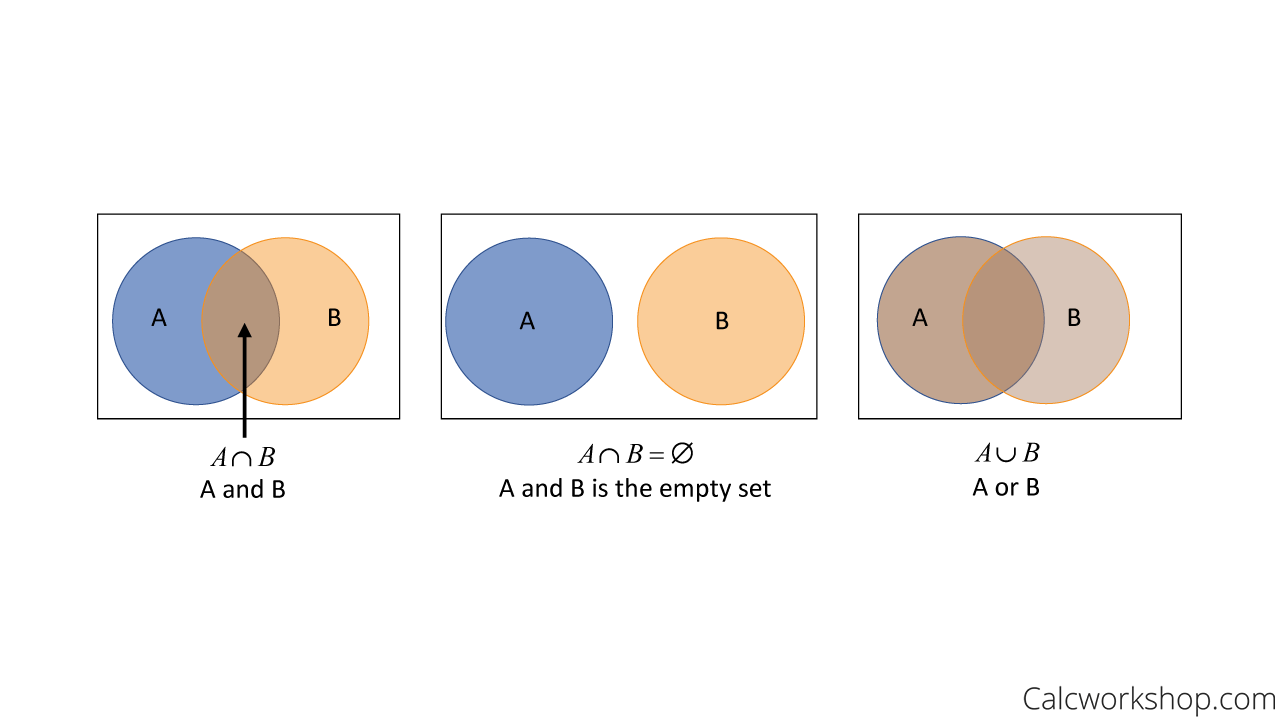
Venn Diagram Union And Intersection
Example – Rolling a Die
This is best illustrated with an example.
Using our previous example of rolling a fair die, which gives us a sample space of S={1,2,3,4,5,6}, let’s find the following two events: A={all the numbers less than 4} and B={all odd numbers}. This means that A={1,2,3} and B={1,3,5}.
So, what’s the intersection of A and B, and what is the union of A and B?
The intersection of A and B, are all the elements that they have in common, which would be {1,3}.
And the union of A and B are a complete list of elements that are in A or B or in both A and B. This means the union of A and B is {1,2,3,5}
Disjoint Events
But what happens if the two events have nothing in common?
This is called disjoint or mutually exclusive events. The two events have no outcomes in common and therefore, can never occur simultaneously.
Problem
For example, if we rolled a fair die with the sample space {1,2,3,4,5,6} and if event A represents the all even outcome (i.e., A={2,4,6}) and event B represents the odd outcomes (i.e., B={1,3,5}). What is the possibility that A and B happen at the same time?
Solution
Since A and B do not have any common numbers, we would say that these events are mutually exclusive (disjoint), and the likelihood that A and B can happen simultaneously is zero.
Together we will learn to identify sample spaces, events, and sample points, as well as determine the number of outcomes using the counting principle. We will learn how to create tree diagrams and Venn diagrams, identify intersections, unions, and disjoint events, and use the complement rule as they relate to sample spaces and probabilities.
Sample Space – Lesson & Examples (Video)
52 min
- Introduction to Video: Sample Space and Events
- 00:00:39 – Identifying sample points and sample spaces (Examples #1-3)
- Exclusive Content for Members Only
- 00:07:16 – Identifying statements and rules for large or infinite sample spaces (Examples #4-5)
- 00:14:07 – What is an event? How do we identify subspaces (Example #6)
- 00:18:27 – Identify the sample space and desired events (Examples #7-8)
- 00:25:33 – Finding complements of an event (Example #9)
- 00:28:31 – Identify the complement of each event (Examples #10-11)
- 00:31:19 – Overview of Intersection, Union and Disjoint Events and Venn Diagrams
- 00:38:06 – Identify the Intersection and Union or Shade the Venn Diagram (Examples #12-15)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.