Did you know that conditional probability occurs when we change the sample space?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s true!
Let me explain.
Example of Probability
Suppose our sample space is a class of high school students, where we desire to determine the proportion of people in the class who do their laundry.
What do we do?

Statistic Probability Formula
Example of Conditional Probability
But now we want to take it a step further. What do we do if we’re going to find the proportion of male students only who do their laundry?
Notice what we did… we reduced our sample size as discussed by Richland Community College.

Conditional Probability Formula Examples
Instead of looking at every student (males and females), we focused on just the male students in the class, and from there, we sought to determine those who did their laundry.
And this is the idea behind conditional probabilities!
Conditional Probability Notation
Let’s look at how we write conditional probability in statistics:
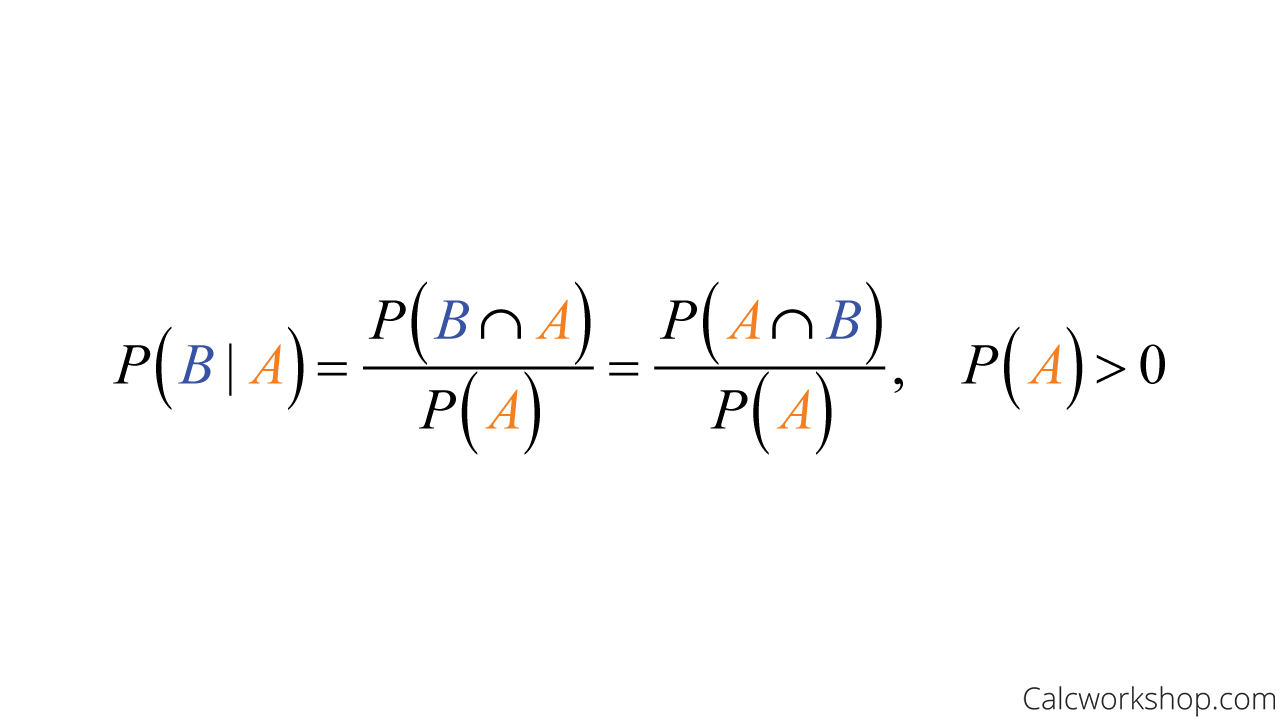
Formula For Conditional Probability
There are several ways we can read this formula:
- Probability of B given A
- Probability of A is B
- Probability of B within A
- Probability of B when selecting from within A only
And what’s so cool about conditional probability is that it’s not limited to sample spaces with equally likely outcomes. In other words, this means that the probability of observing events B and A is the probability of observing A, multiplied by the probability of observing B, given that you have observed A. This is called the chain rule for conditional probability.
Multiplication Rule Of Probability
And this leads us to the Multiplication Rule, which is the probability of the intersection of two events (i.e., the overlap between two events). In other words, it’s the collection of outcomes that are common to both.
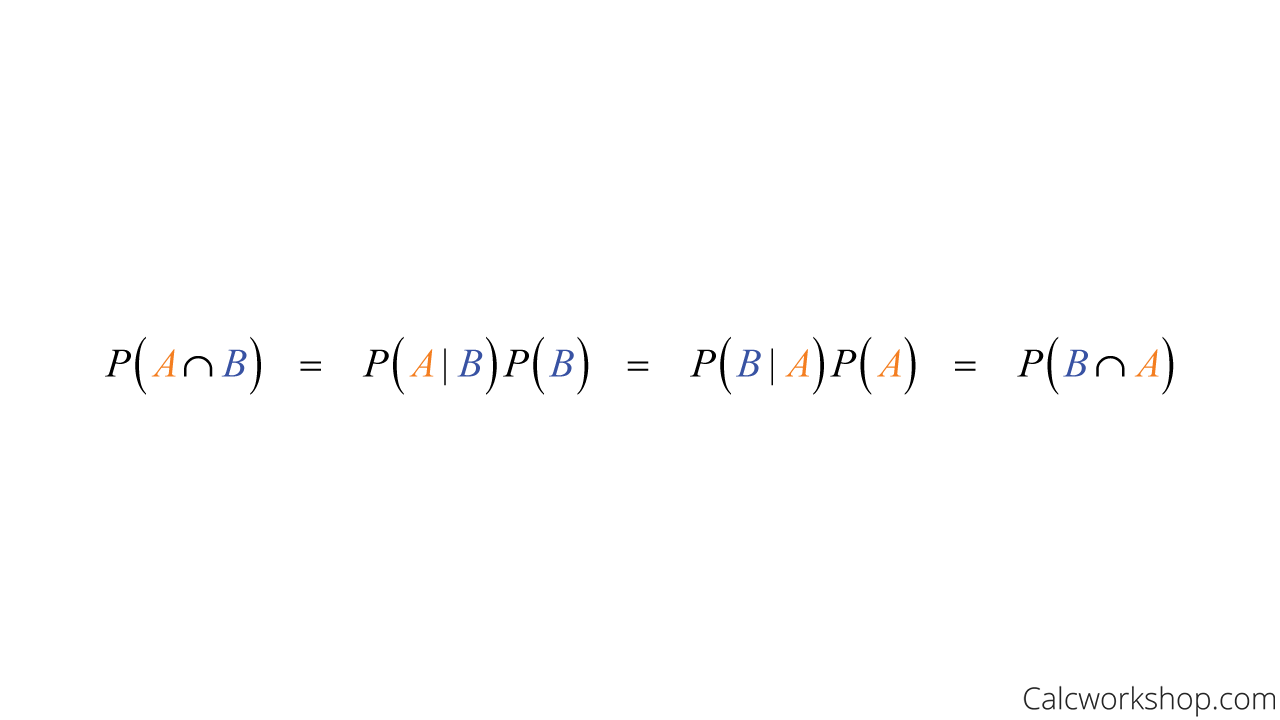
Multiplication Rule Probability
Additionally, two events, A and B, are independent if and only if:
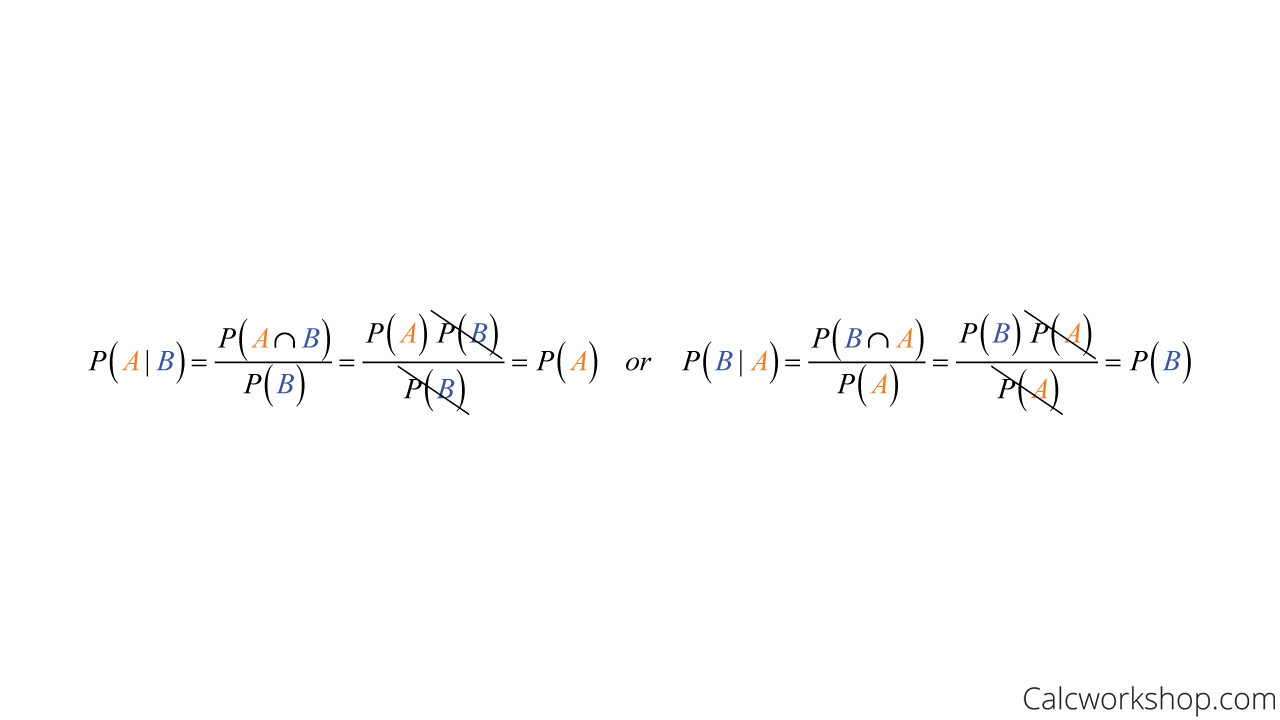
Independent Probability Formula
Independent Vs Dependent Events
Now, let’s remind ourselves of the difference between dependent and independent.
Independent events are when one event does not affect the probability of the other event occurring, like flipping a coin twice. The outcome of the first flip does not affect the result of the second flip.
Dependent events are when one event influences the probability of an event occurring. For example, the higher the chance of rain in the forecast means the higher chance of getting wet when outside. The rain affects you getting wet.
But I must caution you! Independence does not mean disjoint (mutually exclusive)! In fact, disjoint events are dependent events.
Example #1 – Two Way Table
Why don’t we look at a few examples!
A class of 40 students was asked, “do you like school?” The results of the survey are recorded in the two-way table.

Two Way Table
First, let’s find the probability a student likes school given they are male.

Two Way Table Conditional Probability Example 1
And, secondly, let’s find the probability a student is female given they dislike school.

Two Way Table Conditional Probability Example 2
Notice that the key to understanding conditional probability is to shrink or change your sample space.
Now let’s look at how we would find conditional probability given a Venn diagram.
Example #2 – Venn Diagram
Suppose there are three sports teams at school:
- Football
- Basketball
- Track
If it is known that:
- 15 students play football.
- 12 play basketball.
- Ten run track.
- Eight play football and basketball.
- Four play football and run track.
- Four play basketball and run track.
- Three students play all three sports.
Let’s set up a Venn Diagram that illustrates this scenario.
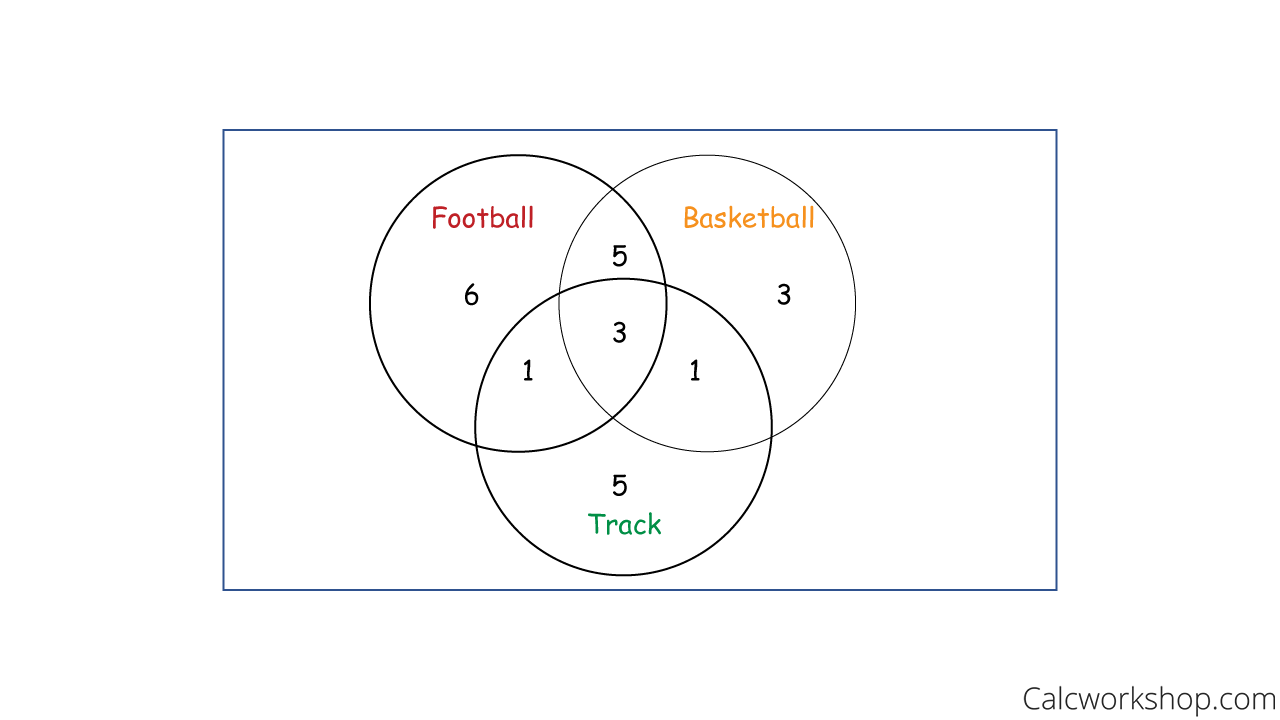
Joint Probability Venn Diagram
Now, let’s find the probability that a student plays football and basketball.
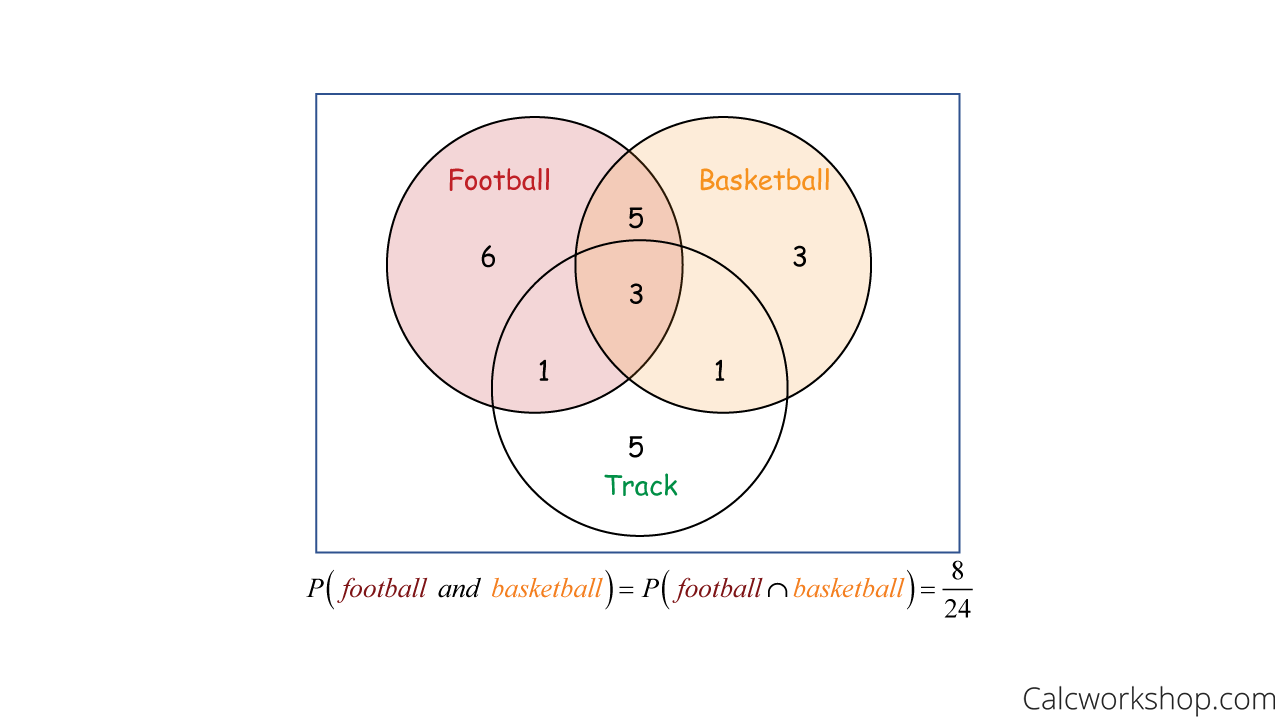
Probability Venn Diagram Multiplication Rule
Next, let’s determine the probability that a student plays football or basketball.
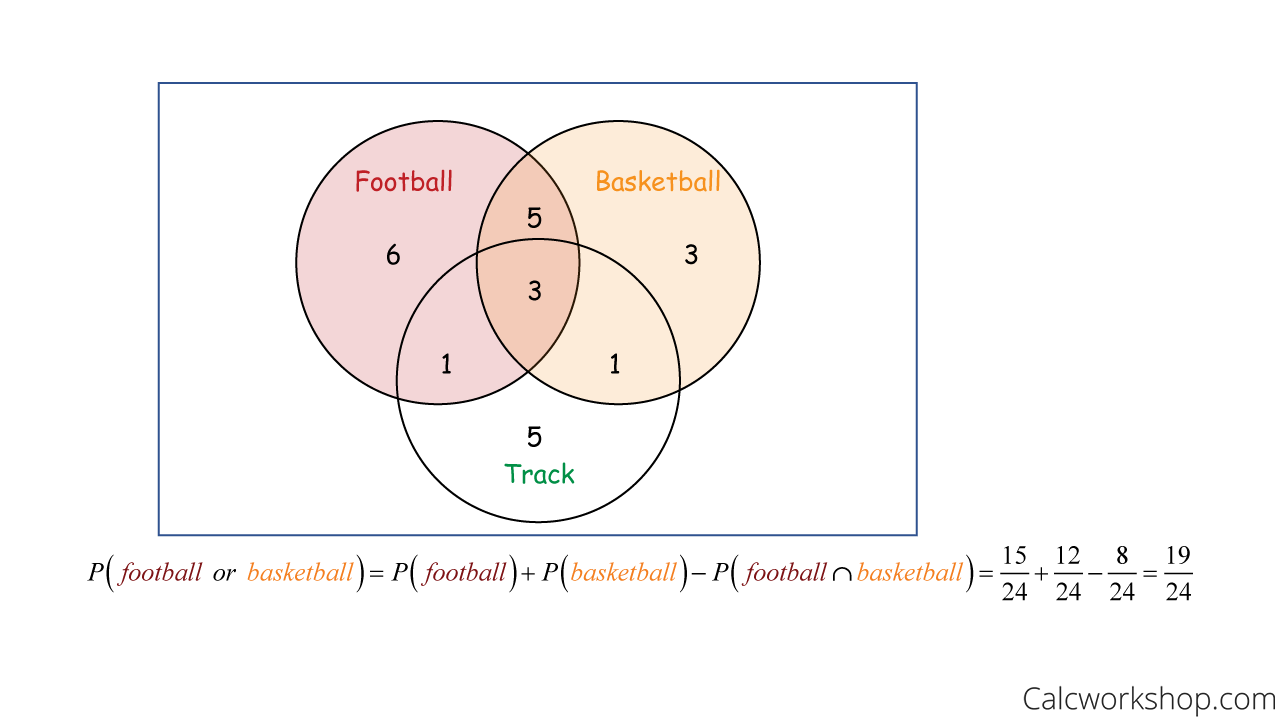
Probability Venn Diagram Additive Rule
And what is the probability a student runs track given that they are on the football team?
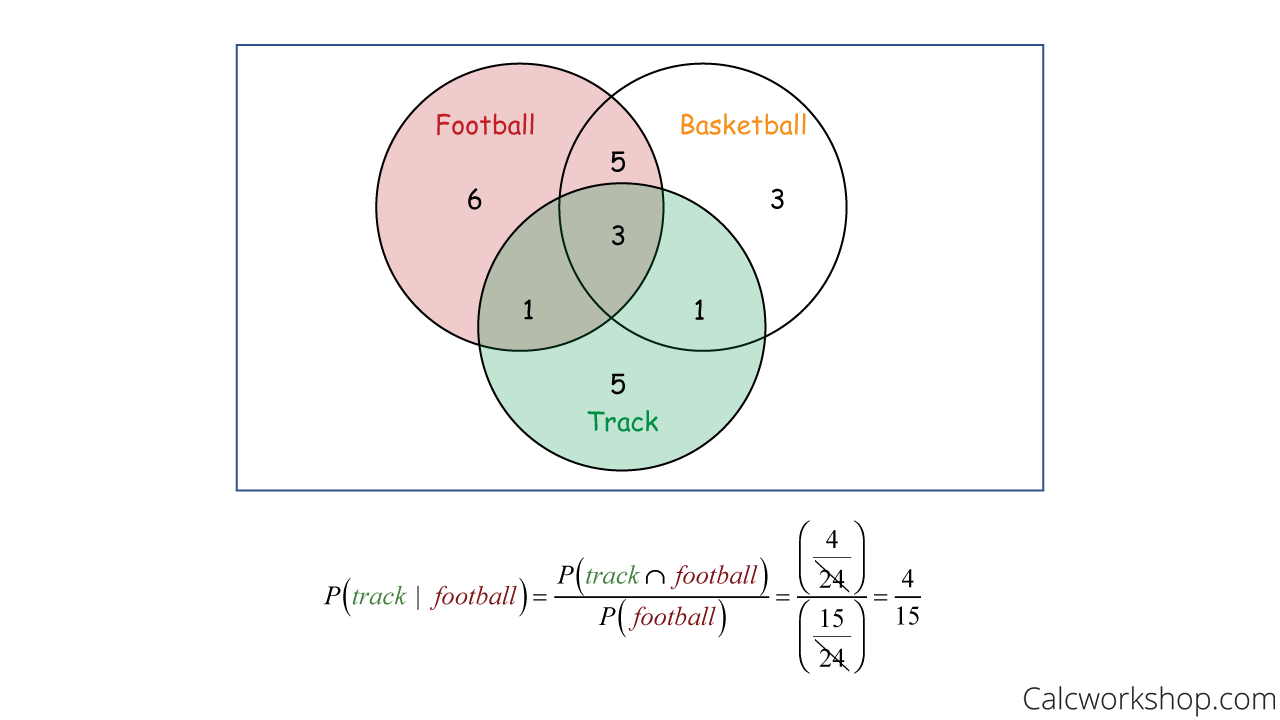
Conditional Probability Venn Diagram
How would we handle conditional probability and the complement rule?
Example #3 – Probability Notation
Suppose a new device to filter unwanted impurities in drinking water is 93% accurate. This could mean several things. For example:
- This could imply that 93% of impure water is filtered.
- Or 93% of filtered water is contaminated.
- Or 93% of pure water is unfiltered.
Express each of these statements using conditional probability notation:
First, we need to identify our events.
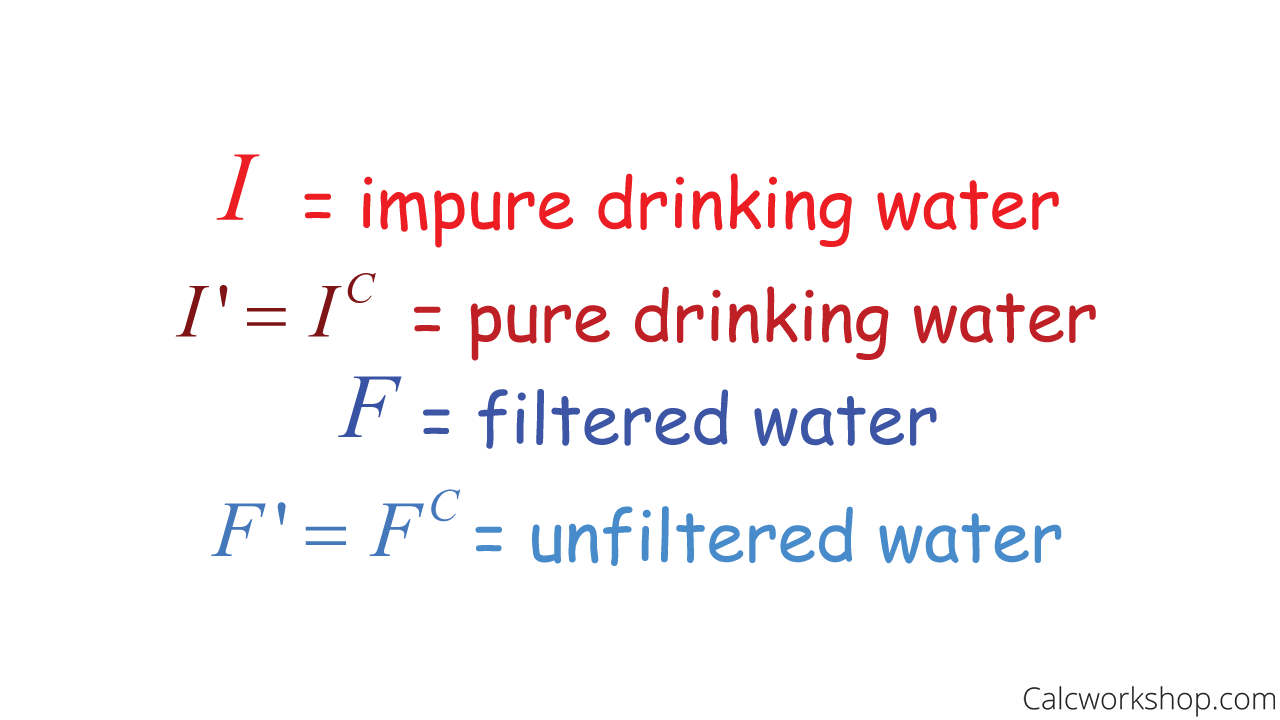
Complement Rule Example
Now, let’s rewrite our statements and express each using conditional probability notation
- 93% of impure water is filtered means we want to find the probability that the water is filtered given that the water is polluted.
- 93% of filtered water is impure means we want to find the probability that the water is dirty, given that the water is filtered.
- 93% of pure water is unfiltered means we want to find the probability that the water is not filtered, given that the water is pure.
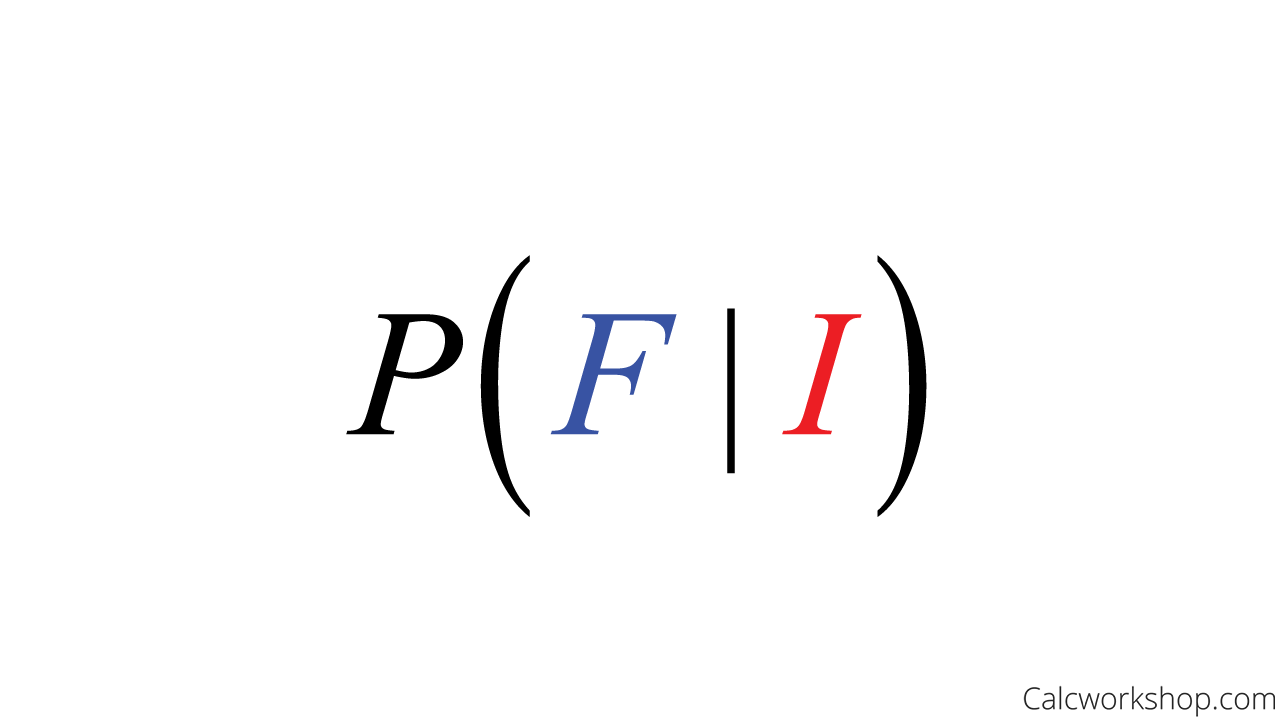
Conditional Probability Notation Filtered Given Impure
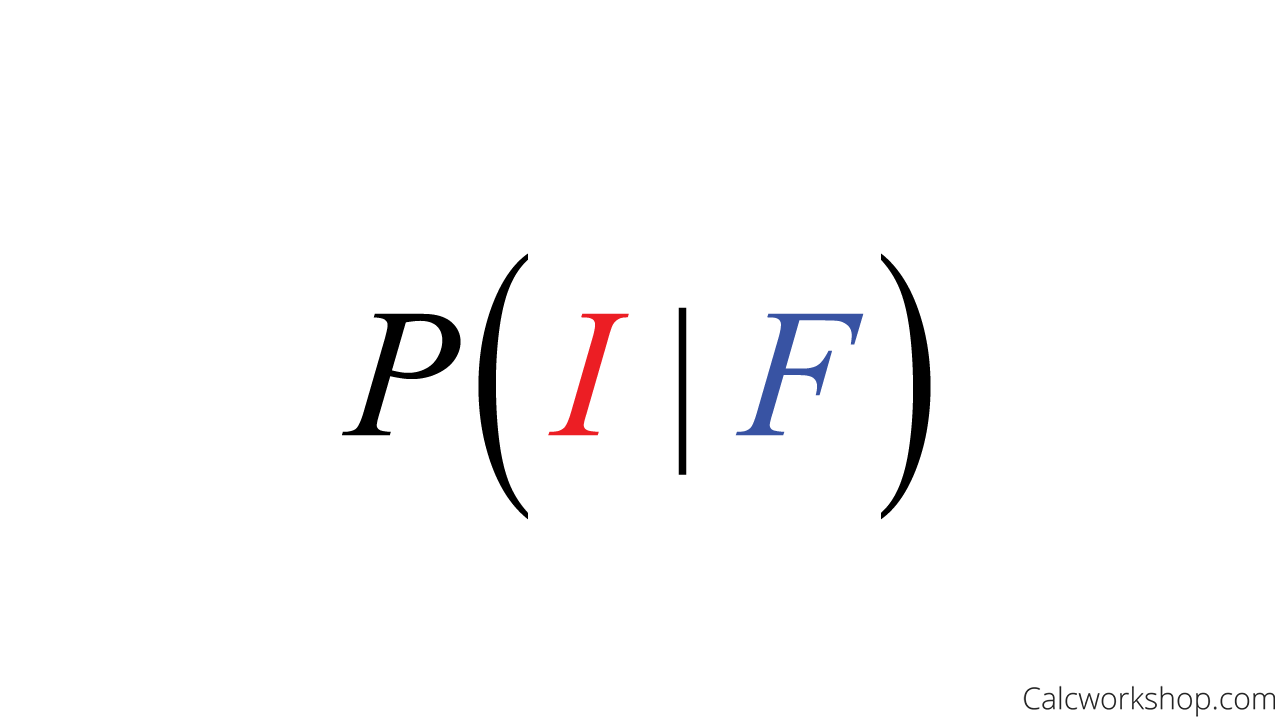
Conditional Probability Notation Impure Given Filtered
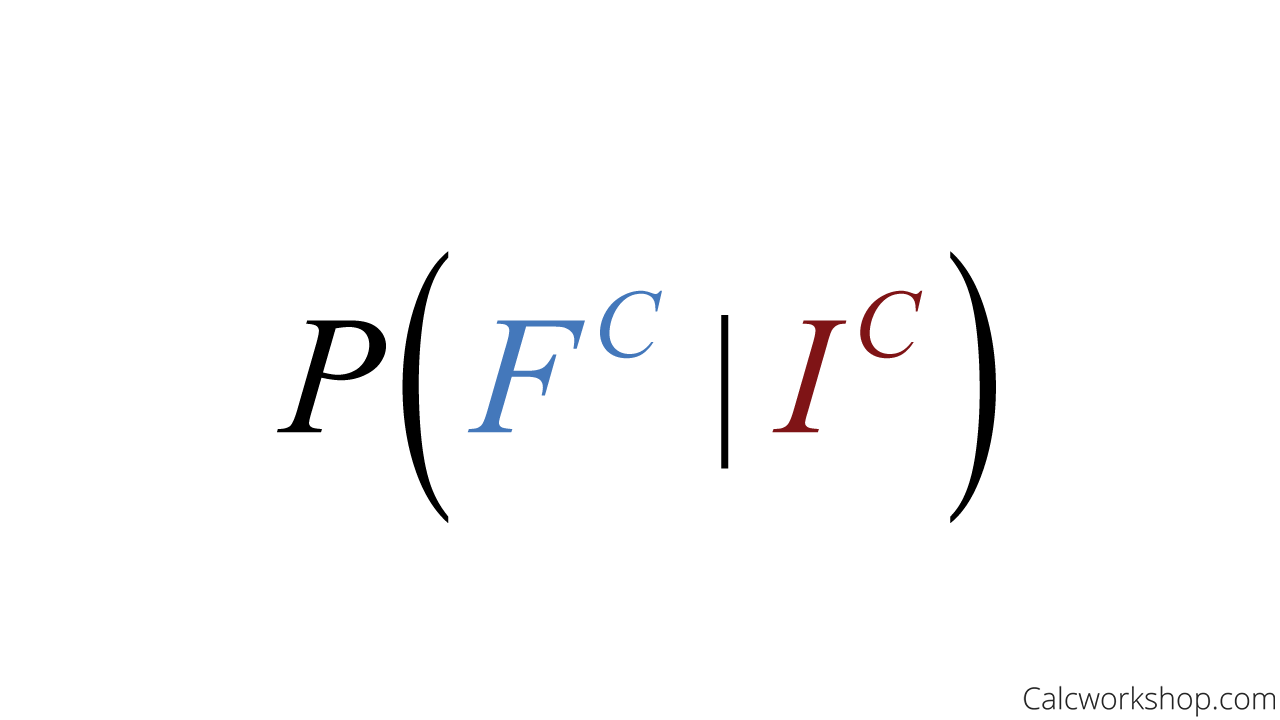
Conditional Probability Complement Unfiltered Given Pure
Together we will work through countless examples, using:
- Two-Way Tables
- Venn Diagrams
- Tree Diagrams
- And Even Circuits
So that we can solve various probability and conditional probability problems.
Let’s get to it!
Conditional Probability – Lesson & Examples (Video)
1 hr 43 min
- Introduction to Video: Conditional Probability
- 00:00:31 – Overview of Conditional Probability, Multiplication Rule, Independence and Dependence
- Exclusive Content for Members Only
- 00:16:43 – Find the probability using the addition rule and multiplication rule given tables (Examples #1-2)
- 00:38:14 – Find the probability and conditional probability (Example #3)
- 00:49:12 – Create a Venn diagram and find the conditional probability (Example #4)
- 01:01:47 – Determine the probability of an event by creating a tree diagram and using independence (Example #5)
- 01:12:02 – Find the probability by using a geometric series and the complement rule (Example #6)
- 01:25:31 – Identify the probability given a two-way table (Example #7)
- 00:56:09 – Determine the probability of an electrical circuit (Example #8)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.