What is Bayes’ Theorem?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
To best understand Bayes’ Theorem, also referred to as Bayes’ Rule, I find it helpful to start with a story.
In Harry Potter and the Goblet of Fire, the fourth book in the Harry Potter series by J.K. Rowling, the Dark Mark has been released over the Quidditch World cup, and total pandemonium has ensued.
Harry, Hermione, Ron, and Winky, the scared house-elf, have all been found at the crime scene.
Moreover, there is the discovery of a wand in Winky’s hand. But is she to blame for the dastardly deed?
While many of you already know the outcome of this part of the story, let’s assume you don’t for a moment – and play along just a bit longer. In other words, let’s pretend you are a Ministry wizard or witch and have happened upon the scene, and it is up to you to solve the crime.
Where do you begin?
Seeing that you are a very clever witch or wizard, you quickly employ bayesian statistics to help you explain this mystery.
What? How?
How To Use Bayes Rule?
First, let’s take a look at our suspects:
Now, let’s present our evidence – the wand.
Your job is to determine the likelihood that each suspect is responsible for conjuring the Dark Mark, given the fact the wand was found at the scene of the crime.
We do this by reversing the question. Instead of saying, what is the chance that Winky committed the crime (if B is true), given the discovery of the wand (A is true), but rather, if the wand is real (if A is true), what is the probability that Winky conjured the Dark Mark (B is true)?
At first glance, it appears that these are the same question, but mathematically, the slight change or reversal helps us solve the puzzle and is the key to understanding Bayes’ Rule!
Definition
Bayes’ Theorem states when a sample is a disjoint union of events, and event A overlaps this disjoint union, then the probability that one of the disjoint partitioned events is true given A is true, is:
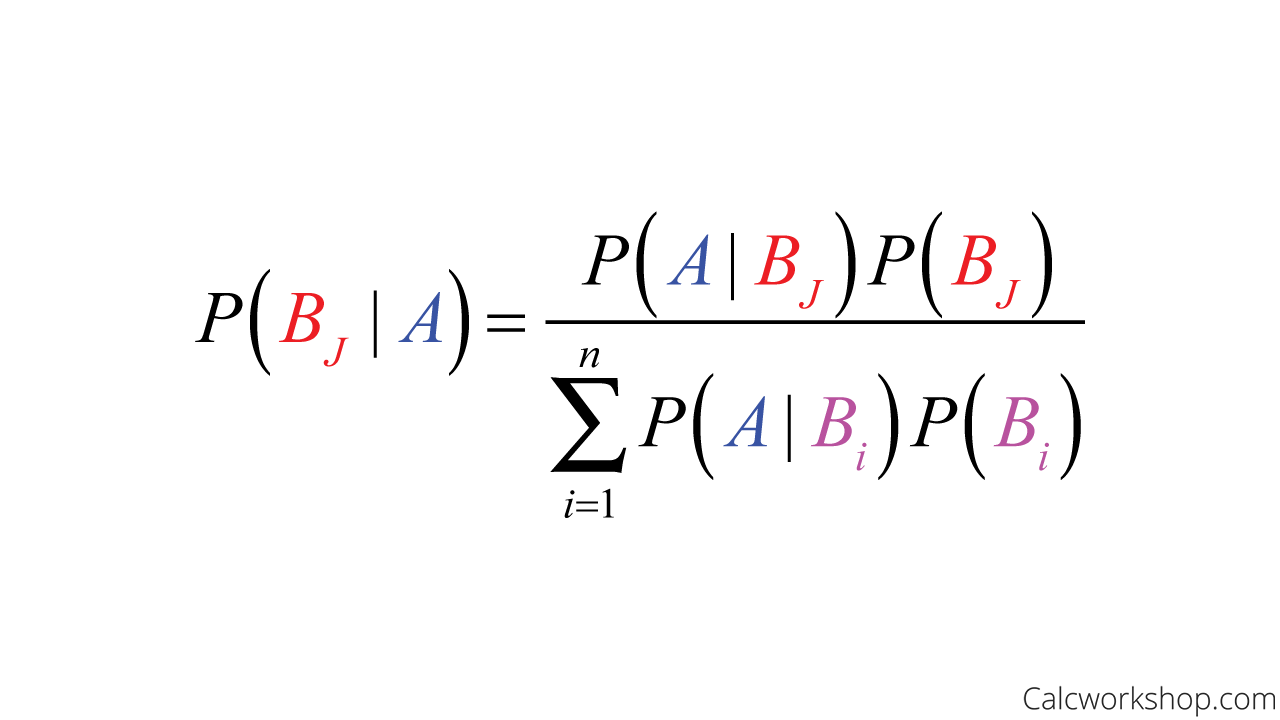
Bayes Theorem Formula
For example, the disjoint union of events is the suspects: Harry, Hermione, Ron, Winky, or a mystery suspect.
And event A that overlaps this disjoint partitioned union is the wand. Therefore, all Bayes’ Theorem says is, “if the wand is true, what is the probability that one of the suspects is true?”
That’s it!
When To Use Bayes Theorem?
So, Bayes’ Rule represents the probability of an event based on the prior knowledge of the conditions that might be related to that event, as Analytics Vidhya accurately states.
If we already know the conditional probability, we use Bayes’ Theorem to find the reverse probabilities. All this means is that we are going to use a Tree Diagram in reverse.
How Do We Use Bayes’ Theorem?
There are various ways to use Bayes’ Rule, such as Venn diagrams and Punnett squares, but I think the easiest way to understand how this works is to picture a tree diagram. We’re going to start at the end branches and backtrack along the branch-stems to find the beginning.
Example – Tree Diagram
While it is known that in a criminal trial, it must be shown that a defendant is guilty beyond a reasonable doubt (i.e., innocent until proven guilty), let’s assume that in a criminal trial by jury, the probability the defendant is convicted, given they are guilty, is 82%.
The probability that the defendant is acquitted, given innocence, is 80%.
And, suppose that 85% of all defendants are indeed guilty. Now, suppose a particular defendant is convicted of a crime. Find the probability they are innocent.
First, let’s create a tree diagram to help us make sense of all the information we have been given.
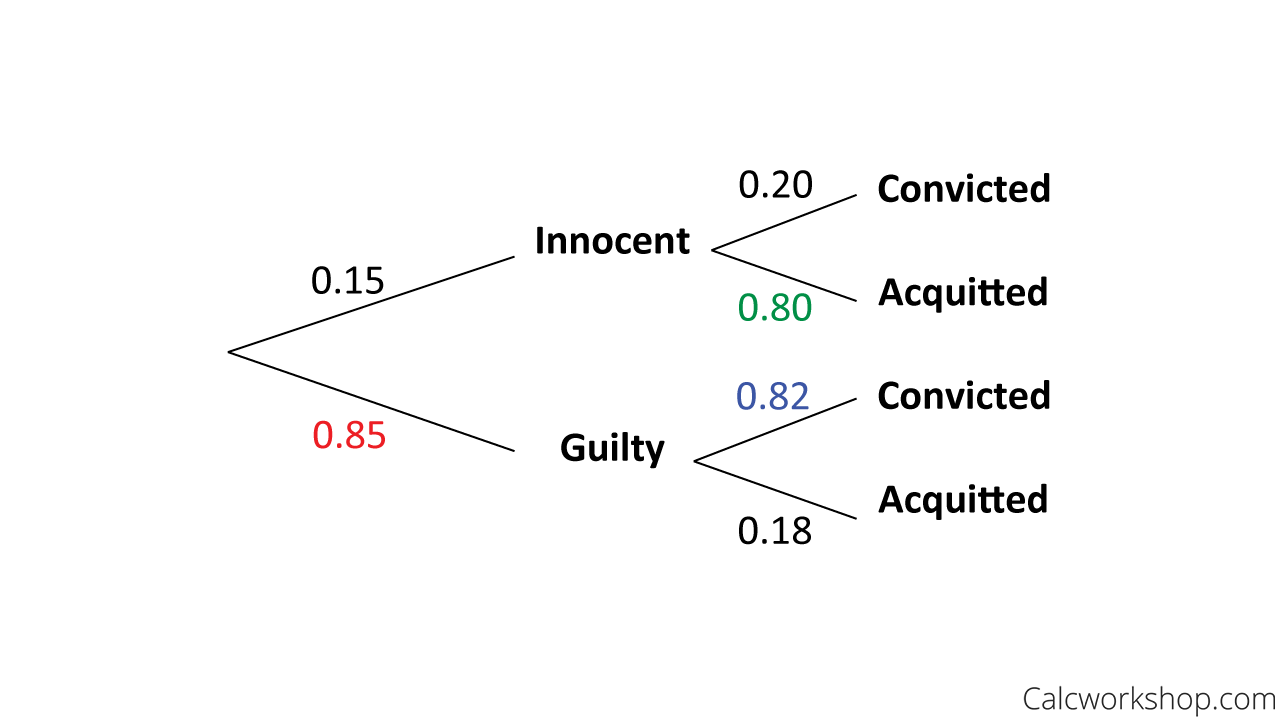
Bayes Theorem Tree Diagram
Now, we are ready to answer the question, “supposing a defendant is convicted, find the probability the defendant is innocent.” All this means is that we are being asked to find the probability of innocence, given conviction. So, we will use Bayes’ Rule while working backward along our tree branches, as illustrated below.
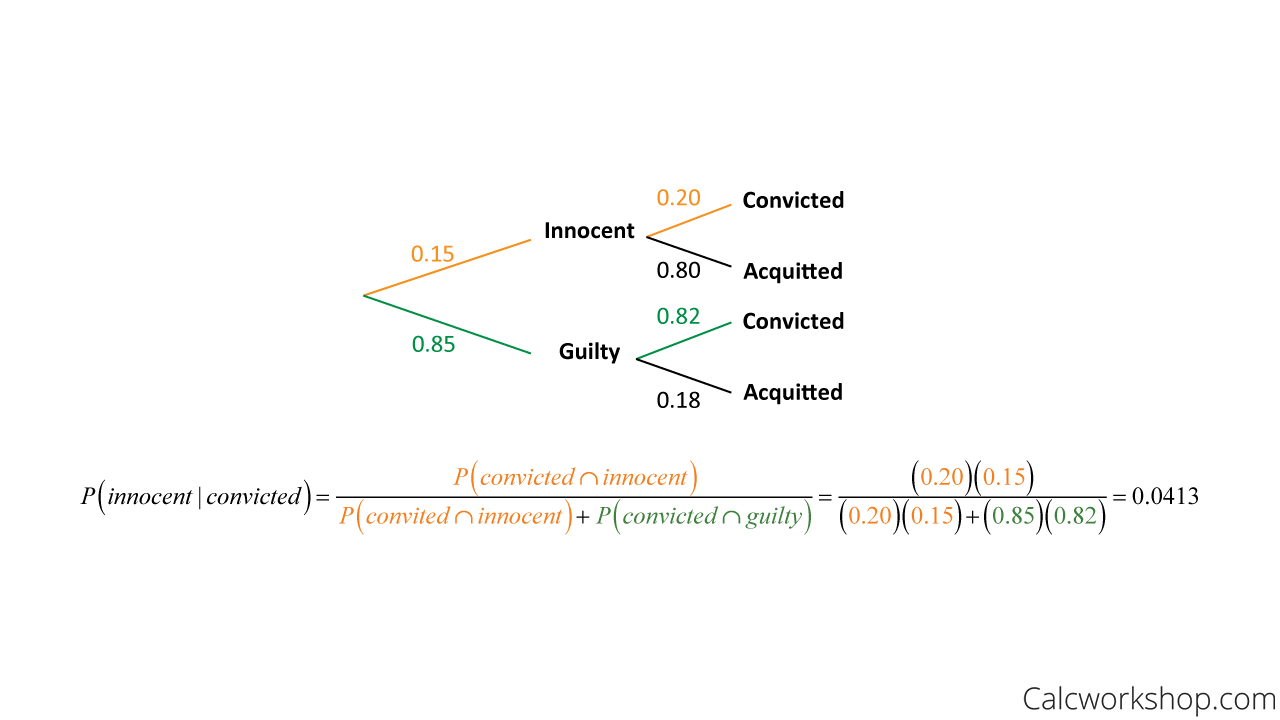
Bayes Theorem Conditional Probability
This means that the likelihood a defendant is found guilty, when in fact they are innocent, is 4.13%.
Now another incredibly important application of Bayes’ Theorem is found with sensitivity, specificity, and prevalence as it applies to positivity rates for a disease.
- Sensitivity is the actual positive rate or the probability that a person tests positive for a disease when they do indeed have it.
- Specificity is the true negative rate or the probability that a person tests negative for a disease when they do not have the condition.
- Prevalence is the probability of having the disease.

Prevalence, Sensitivity, and Specificity
Example – Positivity Rate
Okay, so let’s see how Bayes’ rule helps us to determine the correct positivity rate.
Assume a new test is developed for cancer detection with sensitivity 0.79 and specificity 0.95, with prevalence 0.04. Determine the likelihood that an individual has cancer if their test result is positive.
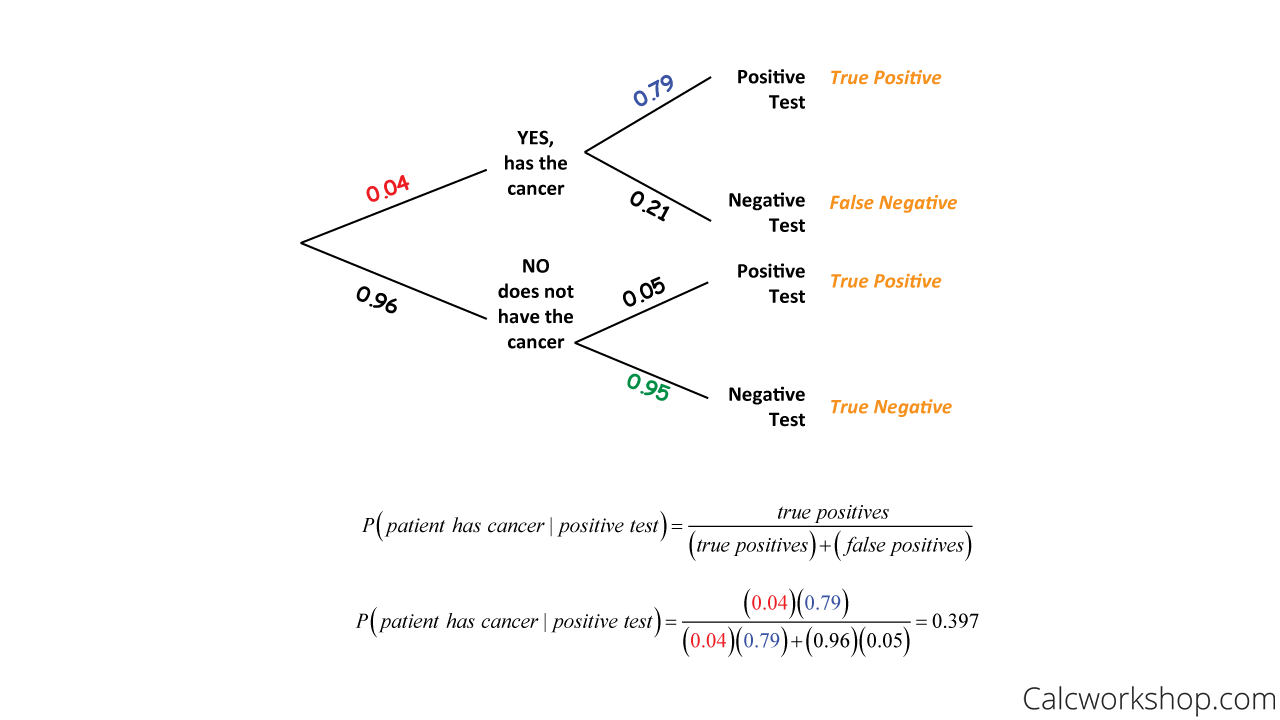
Understanding Sensitivity And Specificity From A Tree Diagram
So, given that this particular test is positive, the probability that an individual has cancer is about 39.7%
Together in this video, we will use two-way tables and tree diagrams to assist us in applying Bayes’ rule.
Additionally, we will walk through countless examples in detail as we endeavor to find the probability of an event based on prior knowledge of conditions related to the event and learn how to identify prevalence, specificity, and sensitivity correctly.
Bayes Theorem – Lesson & Examples (Video)
1 hr 17 min
- Introduction to Video: Bayes’s Rule
- 00:00:24 – Overview of Total Probability Theorem and Bayes’s Rule
- Exclusive Content for Members Only
- 00:09:12 – Use Bayes’s Rule to find the probability a product is made by a particular machine (Example #1)
- 00:24:59 – Use Bayes’s Theorem to find the probability (Examples #2-3)
- 00:38:04 – If a random product is found defective, which plan is most likely responsible? (Example #4)
- 00:50:17 – Find the probability using Bayes’s Rule (Examples #5-6)
- 01:03:49 – Overview of Prevalence, Specificity and Sensitivity
- 01:07:25 – Given the prevalence, specificity and sensitivity of a disease create a tree diagram and find the probability (Example #7)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.