Area of a Regular Polygon
17 Step-by-Step Examples!

Wanna know how to find the area of a regular polygon?

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

The apothem holds the key.

Wait, what’s an apothem?

Let’s find out!

The way we find the area of any regular polygon is by placing it inside of a circle.

Why?

Because when we place a regular polygon inside a circle, we can find the center of the polygon, which will then allow us to divide the polygon into smaller right triangles.

Center of a Regular Polygon

Remember, a regular polygon is one that is both equilateral and equiangular, and the center of a regular polygon is the center of the circumscribed and inscribed circles.

What is so cool is that we can now create smaller triangles by drawing a radius from the center of the circle to each vertex of our polygon. These radii are congruent, and they help to form the central angle.

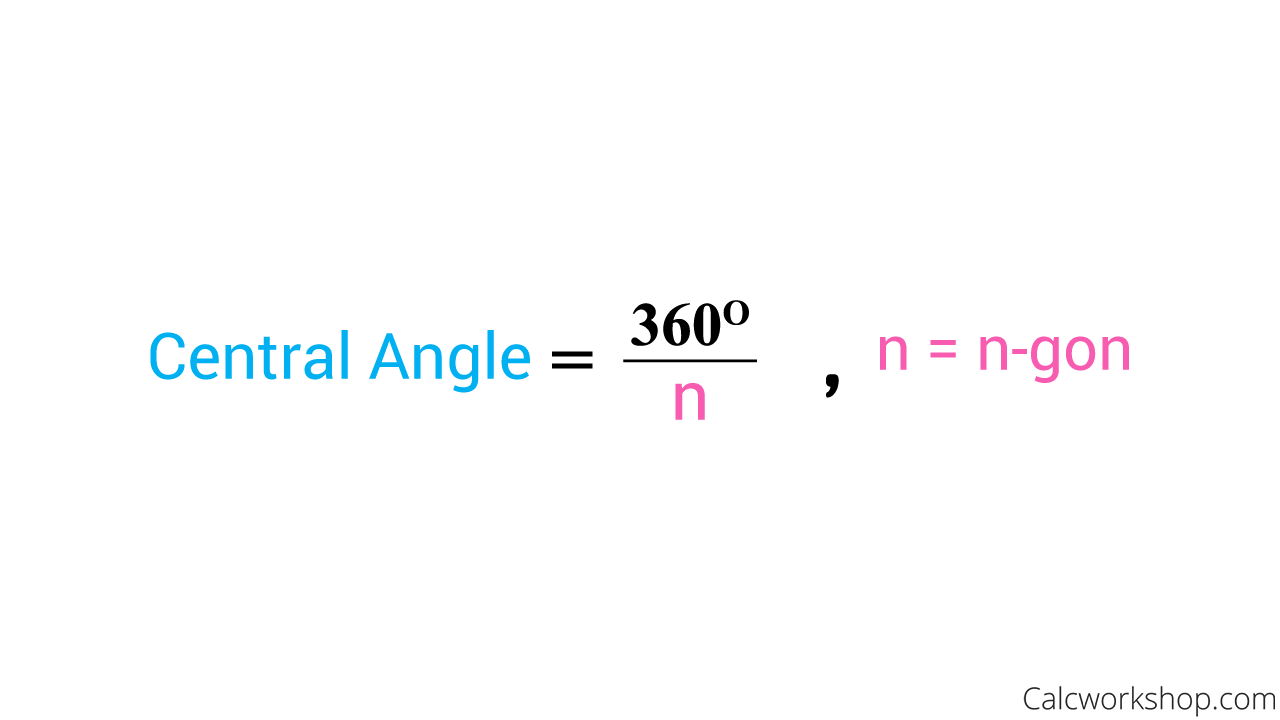
Central Angle Formula

Additionally, if we drop a perpendicular segment from the center to the side of the polygon, we have now created smaller right triangles. What is important to note, is that this perpendicular segment, called the apothem, bisects the central angle and the side of the polygon, creating the midpoint of the side.

Area of a Regular Polygon

Area of a Regular Polygon Formula

However, where does this formula come from?

Well, since we break a regular polygon into smaller triangles, we notice that the side of the polygon is the base of the triangle, and the apothem is the height of the triangle. And since the area of a right triangle is one-half the base times the height, the area of one triangle is one-half the side length times the apothem, as Math is Fun accurately states.

This means the area of the regular polygon is nothing more than the sum of the area of each of these smaller right triangles!

Before we get to the video, let’s go over a few examples.

Types of Problems

Example #1 – How To Find The Apothem?

To find the apothem of the square below we first find the center by intersecting the diagonals. The apothem is the perpendicular distance from the center to one of the sides. To find the measure of the apothem, we use our knowledge of right triangles and trigonometry, a seen below.

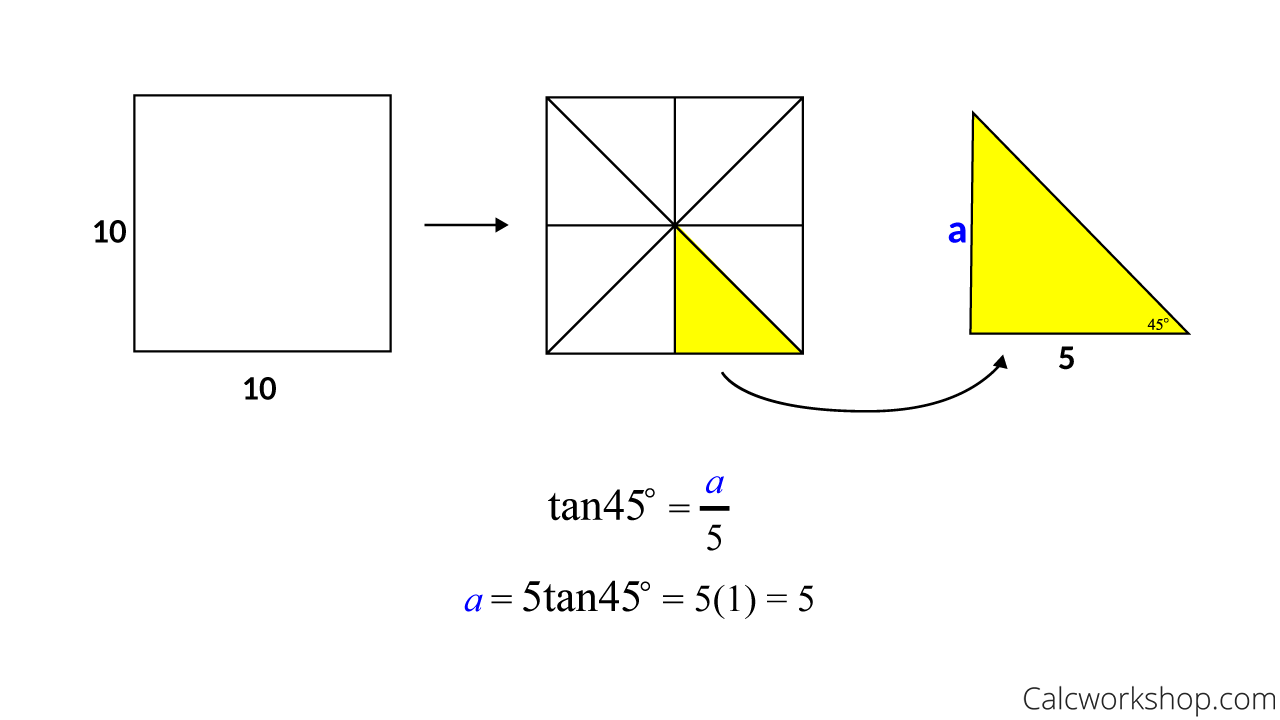
How To Find The Apothem Of A Regular Polygon

Example #2 – How To Find The Area Of A Hexagon?

To find the area of a regular hexagon, or any regular polygon, we use the formula that says Area = one-half the product of the apothem and perimeter. As shown below, this means that we must find the perimeter (distance all the way around the hexagon) and the measure of the apothem using right triangles and trigonometry.

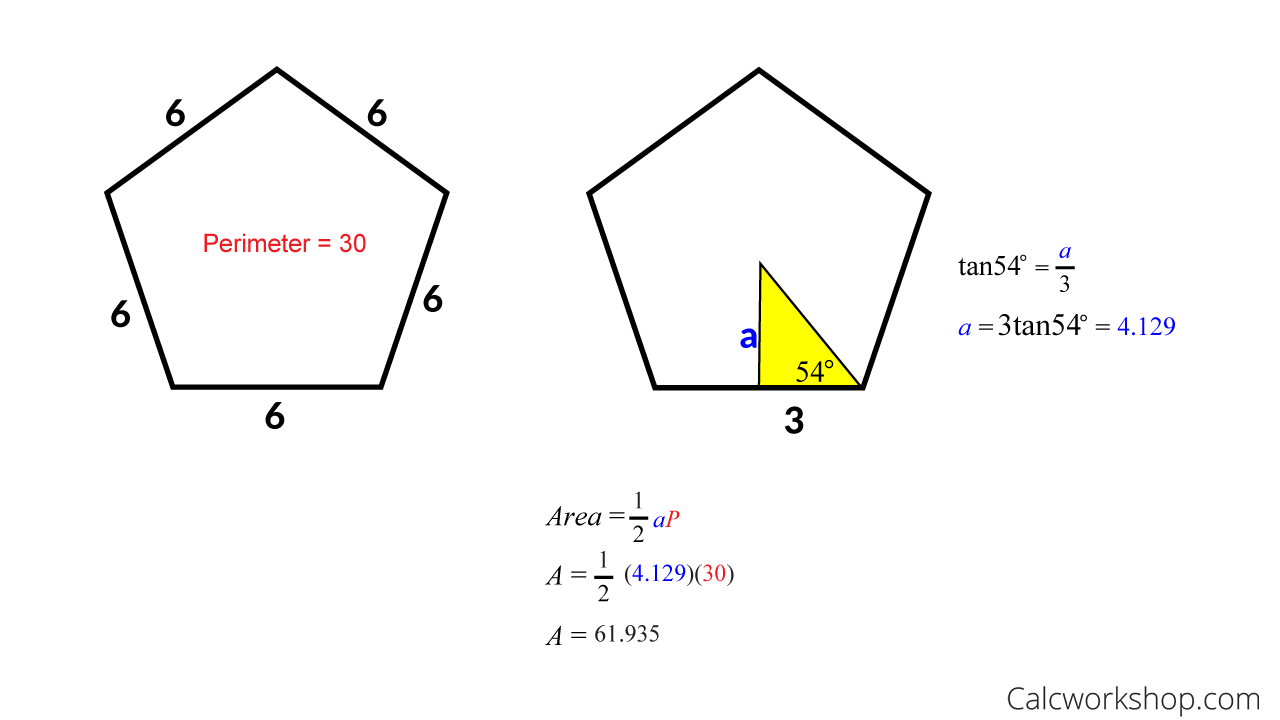
Area of a Hexagon

In the video below, you’re going to learn:

1. How to find the central angle of a regular polygon.
2. Understand how to solve for the radius, side length or apothem for any regular polygon.
3. Find the area of any regular polygon by using special right triangles, trigonometric ratios (i.e., SOH-CAH-TOA), and the Pythagorean theorem.

Video – Lesson & Examples

1 hr 23 min

• Introduction to Video: Area of Regular Polygons
• 00:00:39 – Formulas for finding Central Angles, Apothems, and Polygon Areas
• Exclusive Content for Member’s Only

• 00:11:33 – How to find the measure of a central angle given a regular polygon (Examples #1-4)
• 00:24:04 – Find the area of the regular polygon given the apothem and perimeter (Examples #5-7)
• 00:27:43 – Find the length of the apothem for the given square (Example #8)
• 00:32:43 – Find the indicated measure for a regular polygon (Examples #9-10)
• 00:47:16 – Find the area of the regular polygon (Examples #11-12)
• 01:02:06 – Calculate the area of the regular polygon (Examples #13-14)
• 01:17:43 – Using ratios to find the perimeter and area of similar polygons (Examples #15-17)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions